La pose du problème. On entende par le terme «des grands passages» les passages
des lignes aériennes du transport de l’énergie électrique (LA) dans les conditions du pays plat par de larges espaces d'eau (les rivières
navigables et non-navigables, les golfes, les détroits maritimes et d'autres obstacles d'eau) et dans les conditions du pays de montagne par
les gorges diverses.
Le calcul d’un grand passage de LA consiste en définition des gabarits de la ligne au-dessus de la surface d'eau ou des marques du terrain
de montagnes. En prenant en considération, que par quelque temps les gabarits de calcul des conducteurs au passage diminuent à cause
des déformations résiduelles des conducteurs, le problème initial d’étude doit être résolu avec les plus faibles
erreurs.
L'analyse de la méthode existant. La méthode existant du calcul mécanique de conducteurs des LA dans les portées
ordinaires [1] et pour de grands passages [2] à la base de la théorie d’une ligne à chaîne possède une série des inconvénients.
C'est pourquoi les calculs des conducteurs sur les grands passages des LA avec l'utilisation de la théorie d’une ligne à chaîne peut amener en cas des circonstances
définies aux résultats insuffisamment sûrs. Notamment ce fait a servi de raison pour l'étude de la possibilité importante de l'utilisation de la théorie
d’une chaîne à résistance identique en vue de la résolution du problème d’étude du calcul précis des conducteurs sur les grands
passages des LA.
Comme on le sait, la chaîne à résistance identique s'appelle une chaîne à épaisseur variable possédant l'épaisseur qui
est proportionnelle à la tenue dans chaque point et la probabilité de la rupture est identique dans tous les points de cette chaîne. La théorie d’une chaîne à
résistance identique est plus sévère en comparaison de la théorie d’une ligne à chaîne utilisée à présent. En outre, la théorie
d’une chaîne à résistance identique permet de recevoir les décisions relativement simples de la série de tâches du calcul, soi-disant mécanique,
des conducteurs de LA sur un grand passage qu'est pratiquement peu accessible en cas d’utilisation de la théorie d’une ligne à chaîne.
Le devoir aux élaborations. Proposer les expressions de calcul pour la définition des paramètres pour les grands passages des LA à la base
de la théorie d’une chaîne à résistance identique et les contrôler dans les calculs des grands passages concrets des LA par les espaces d'eau.
L'exposition de la matière principale. Soit le conducteur électrique est suspendu sur deux pylônes à l'hauteur h1 et h2 sur un grand passage
par la rivière. Nous désignerons:
L - la longueur du fil;
l - la distance entre les bases des pylônes;
γ - la charge spécifique de la masse du fil.
Nous recevrons l'équation pour la courbe de la flèche de fil à la base de la théorie d’une chaîne à résistance identique et aussi
les expressions pour le calcul de la flèche la plus grand de fil sur le passage et pour le calcul des contraintes dans le conducteur.
Figure 1 - L'esquisse du grand passage d’une LA
Était reçu plus tôt, qu’en points de la suspension du conducteur à une hauteur dans les axes rectangulaires
0αβ (fig. 2), les équations d’une chaîne à résistance identique ont l'aspect suivant:
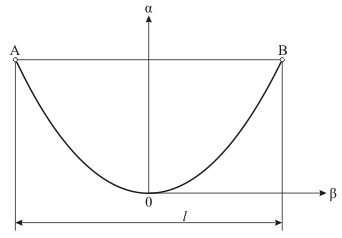
Figure 2 - La courbe de la flèche de fil en axes 0αβ
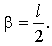
Nous choisissons le système des axes rectangulaires Axy à l’origine en point A de manière que l'axe x soit disposé
horizontalement au plan du fil, mais l'axe y est dirigé verticalement en haut. Les coordonnées du point B nous désignerons par l et
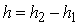(fig. 1).
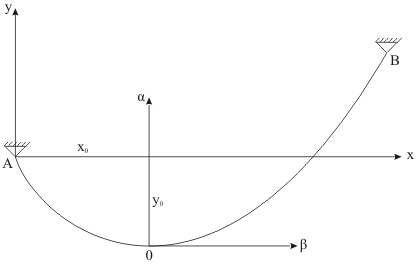
Figure 3 - La courbe de la flèche de fil en axes Axy
Comme il convient de fig. 3:
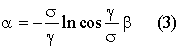
Si introduire de nouvelles coordonnées, l’équation (3) compte tenu de
; 
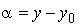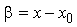accepte l'aspect suivant:
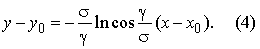
L'équation d’une chaîne à résistance identique, inscrite compte tenu de (3)
contient trois paramètres x0, y0, σ, qui peuvent être définis des conditions aux extrémités du conducteur.
En effet, soit le point B est disposé plus haut le point A. Alors en point A 
, et par conséquent:
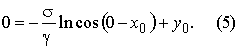
En point B 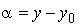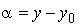, c'est pourquoi:
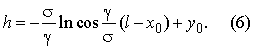
De l'expression (5) nous trouvons la valeur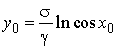 
et la mis à (6), ensuite est disponible:
Définitivement on peut inscrire l'équation (7) pour la courbe de la flèche de fil à l’origine des coordonnées en point A:
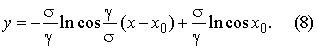
Nous recevrons l'expression de calcul pour la définition des contraintes dans le conducteur.
Puisque dans le système des coordonnées rectangulaires 0αβ (fig. 3)
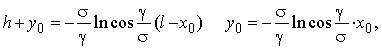
on peut inscrire cela:
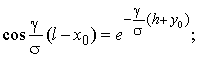
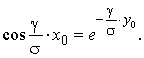
En multipliant les parties droites et celles gauches de ces rapports, nous avons:
Ou bien après avoir simplifié
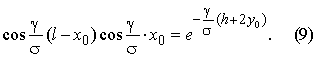
En utilisant (2), nous inscrirons l'expression pour la définition de la longueur du conducteur sur le passage (fig. 3) dans l'aspect suivant:
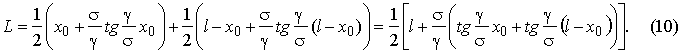
Puisque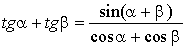 
, on aura:
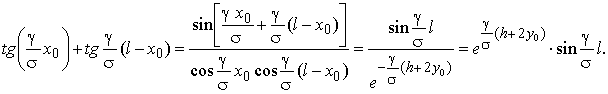
Nous avons définitivement l'expression de calcul pour la définition de la longueur du conducteur sur le passage avec suivant l'aspect:
Nous remarquerons, qu'on peut exprimer la valeur y0 dans les parts de la dénivellation h.
En décidant (11) par rapport à σ par n'importe quelles méthodes connues (par exemple, la méthode de la démi-division), on peut définir les tensions mécaniques dans le conducteurs sur le passage.
Nous passons vers la définition de la flèche la plus grande de fil sur le passage.
Au début nous trouvons la grandeur h0 (fig. 4):
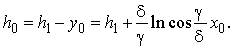
La valeur x0 peut être trouvée de l'équation (7), en la décidant par rapport à x0 par n'importe quel méthode connu.
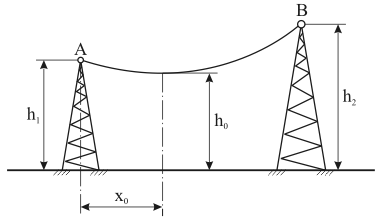
Figure 4 - A la définition de la valeur h0
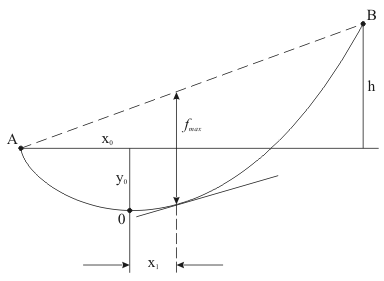
Figure 5 - A la définition de la flèche la plus grand de fil
Une flèche la plus grande de fil (fig. 5) sera en tel point de la courbe, où la tangente vers celle-ci est parallèle à la ligne droite AB (le point С).
Comme on le sait,
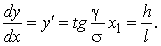
La flèche la plus grande de fil sur le passage peut être défini selon l'expression suivante:
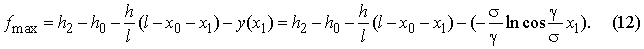
Donc nous avons l'expression de calcul pour la définition de la flèche la plus grande de fil sur le passage dans l'aspect suivant:
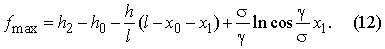
La conclusion. Les résultats reçus à l’aide de la calculatrice sur grand passage de LA 150 кV par le liman de Bugskiy avec l'utilisation des méthodes diverses témoignent que la condition la plus sévère selon le gabarit du conducteur h0 sur le passage de LA par les espaces d'eau apparaît en cas d'utilisation dans les calculs des expressions proposées à la base de la théorie d’une chaîne à résistance identique en comparaison des méthodes actuellement traditionnelle basée sur la théorie d’une ligne à chaîne. Ainsi, en cas de calcul selon la théorie d’une ligne à chaîne dans le projet du grand passage mentionné le gabarit au-dessus du mât de navire fait la grandeur 5,08 m, tandis qu’en cas de calcul selon la théorie d’une chaîne à résistance identique le même gabarit est estimé par la grandeur 4,28 m, ce que dans les circonstances définies peut créer les difficultés pour l'exploitation normale de LA sur ce grand passage.
BIBLIOGRAPHIE
1. Бошнякович А.Д. Механический расчет проводов и тросов линий электропередачи. - М.: Энергия, Ленинградское отд-ние, 1971. - 295с.
2. Бошнякович А.Д. Расчет проводов подстанций и больших переходов ЛЭП. - Л.: Энергия, 1975. - 236с.