Généralités
problème de l'acquisition de données
Lorsqu'on avait une électronique purement analogique il y avait une correspondance directe entre le courant et la déviation du galvanomètre. Dorénavant on souhaite afficher le résultat sous forme numérique, d'une part, et le sauvegarder dans la mémoire d'un système informatique, d'autre part. On va donc être confronté au besoin de réaliser une conversion de la donnée analogique (courant ou tension) en une valeur numérique, c'est à dire codée en binaire. Fonction que l'on réalisera à l'aide d'un convertisseur analogique numérique ou CAN (ADC en anglais pour analogue to digital converter).
Rappelons que cette conversion impliquera un échantillonnage de la grandeur, c'est à dire sa sauvegarde pendant la durée de l'opération de conversion dans un dispositif dénommé généralement échantillonneur-bloqueur, et que la fréquence d'échantillonnage (conditionnée par le temps de conversion du CAN choisi) devra satisfaire aux contraintes du théorème de Shannon si l'on ne souhaite pas perdre d'information.
problème inverse de la commande numérique
Inversement il est de plus en plus fréquent d'afficher une commande sous forme numérique et il faut lui faire correspondre une grandeur analogique de la variable commandée, ce que l'on réalisera via un convertisseur numérique analogique CNA (ou DAC digital to analogue converter).
correspondance analogique-numérique
Avant de présenter les dispositifs nous allons rappeler les principes du codage qui est à la base de ces convertisseurs. Le codage c'est la conversion d'une donnée d'une représentation dans une autre par le biais d'une certaine fonction.
Un nombre réel peut être représenté par l'expression 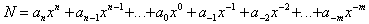 où
x est la base et a un nombre entier compris entre 0 et x-1.
où
x est la base et a un nombre entier compris entre 0 et x-1.
Quand x=10 on a le système décimal et pour x=2 le système binaire, etc.
Dans les CAN et CNA le premier bit (celui de rang n) est appellé MSB (pour most significant bit) et son poids représente la moitié de la pleine échelle du convertisseur, son suivant repésente le quart, etc. Ainsi en huit bits on peut compter de 0 jusqu'à 255 (soit 256 intervales). Le MSB représente le nombre 128 (soit la moitié de 256). Le bit de poids le plus faible LSB (least significant bit) représente la quantité minimale que l'on pourra identifier soit 1. On donne à cette quantité qui va caractériser la résolution du système le nom de quantum. Dans un CAN le quantum c'est en pratique la plus petite variation de la grandeur analogique d'entrée qui va provoquer une variation de 1 unité du code de sortie. On exprime souvent la résolution en pourcentage de la pleine échelle. Ainsi dans un système à 8 bits cette résolution sera 1/256 soit 0.4%.
| nb de bits | 8 | 10 | 12 | 16 |
| nb de points | 256 | 1024 | 4096 | 65536 |
| résolution % | 0.4 | 0.09 | 0.02 | 0.0015 |
Les principales caractéristiques d'un convertisseur:
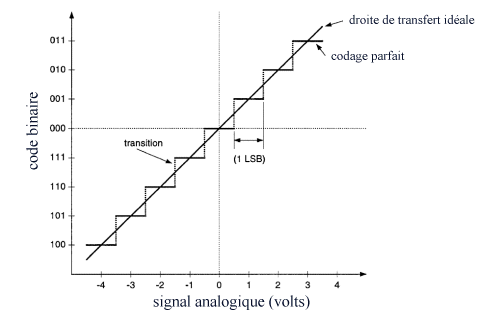
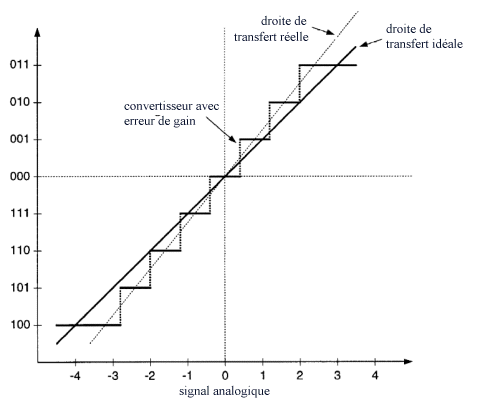
Figure - correspondance entre code numérique et signal analogique (cas idéal) |
- quantum (1/2n)
- linéarité
- pleine échelle 2n-1
- précision 1/2 quantum ou 1 LSB en général
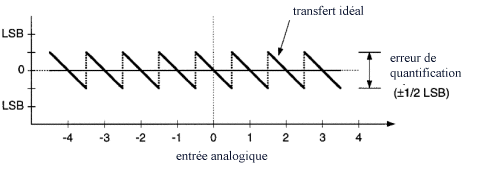
|
-
monotonie c'est à dire l'absence d'erreur de codage faisant qu'un code correspondant à une augmentation de l'entrée de 1 quantum ne soit inférieur au précédent, en d'autres termes caractéristique correspondant au fait que les codes successifs sont constamment croissants.
- temps de conversion : temps au bout duquel une valeur stable est obtenue à 1/2 quantum près.
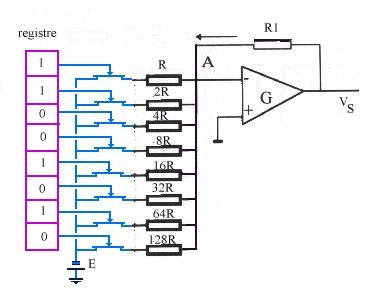
| Convertisseur Numérique Analogique à résistances pondérées principe Il permet de restituer en analogique une grandeur préalablement convertie en binaire (ou générée par un microprocesseur). L'idée de base repose sur le transistor MOS dont la conductance est affectée par le potentiel de sa grille. On va ainsi faire correspondre à un code binaire à n bits n transistors MOS dont les grilles seront affectées respectivement par un bit qui selon qu'il sera 1 ou 0 (c'est à dire le plus souvent 5V ou 0) rendra le transistor conducteur ou non. La quantité numérique est placée dans un registre à n bits qui sera adressé en parallèle sur les n grilles commandant chacune une voie d'un additionneur. On va ainsi faire correspondre à chaque cœfficient an non nul une tension pondérée par une résistance et l'amplificateur va effectuer la somme. |
|
| Ainsi supposons que l'on ait 11001010 (soit 202 en décimal) la tension de sortie sera
Supposons que la tension d'alimentation du CNA soit 10V (c'est à dire la tension maximale que l'on pourra obtenir en sortie pour le code 255 soit 11111111) dans cet exemple la tension Vs serait donc 10 (202/255) = 7.92V, et le quantum serait 39mV d'où évidemment le choix de E, R1 et R (conditionné par la résistance 128R). Les caractéristiques sont celles définies précédemment. Notons que la linéarité résulte de la qualité des résistances et constitue l'une des difficultés de ce système, car sur une telle gamme de résistances ce n'est pas aisé de garantir les valeurs avec une même précision. En outre la conductance du transistor MOS est en série et doit donc être prise en compte dans la résistance pour environ 50W. Or les transistors ne sont pas parfaits et donc peuvent avoir des conductances légèrement différentes. Il en est de même du circuit électronique de lecture du registre qui peut affecter les grilles des MOS avec des tensions légèrement différentes d'où il résulte des conductances différentes. La difficulté est évidemment accrue pour un convertisseur 12 ou 16 bits (dans ce dernier cas la plage est de 1 à 32768 fois R, et l'on voit que si R est choisie égale à 1000 ohms la résistance de plus grande valeur serait de >32MW). En conséquence si la linéarité reste dans la plage du 1/2LSB pour un convertisseur 8 bits c'est quasiment impossible pour un 16 bits qui devra donc être basé sur un autre principe. En outre si la résistance R1 est incorrecte on aura une erreur de gain |
|
| On peut aussi avoir une erreur d'offset qui se traduit par une droite de transfert réelle de pente correcte, mais décalée (parallèle) par rapport à la droite idéale. Notons que ces deux types d'erreur peuvent se trouver aussi bien sur les CNA que sur les CAN (mais avec une origine technologique évidemment différente). En ce qui concerne le temps de conversion il y a des transitoires et parasites dus à la commutation et là encore on peut s'attendre à ce que tous les MOS ne basculent pas en un temps identique, d'où la nécessité d'attendre la stabilité, à 1/2 quantum près, de la valeur finale après application de la commande avant d'exploiter le résultat. CNA à réseau en échelle La structure précédente présentant une difficulté de réalisation on a imaginé un dispositif basé sur un jeu de résistances en échelle pour lequel seules 2 valeurs de résistances, R et 2R, sont nécessaires ce qui facilite l'ajustage et réduit les dérives. Deux architectures voisines ont été implémentées, l'une basée sur une commutation de tension, l'autre, plus rapide, sur une commutation de courant. |
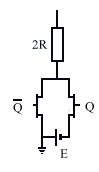
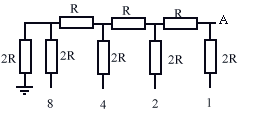
Figure - Principe du réseau en échelle et principe de la commande |
|
On notera que la dernière résistance 2R est toujours connectée à la masse, tandis que les autres correspondent au poids inverse des bits (1, 2, 4, 8, etc).Sur la figure on s'est limité à 4 bits mais il est aisé de comprendre que l'on peut faire n'importe quelle taille d'échelle. Un convertisseur 64 bits est alors parfaitement envisageable. commutation de tension Chaque résistance de valeur 2R est commutable, soit vers la source de tension E, soit vers la masse, grâce à deux transistors MOS connectés respectivement à la sortie Q et la sortie complémentaire Q barre de l'élément de registre leur correspondant. Ainsi si l'une des sorties est à 1 l'autre est à 0 et un seul des transistors MOS est conducteur à la fois. Cette organisation présente plusieurs avantages:
|
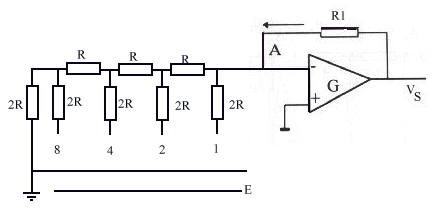
Figure - principe du convertisseur à échelle R/2R |
|
Sur la figure afin d'alléger le dessin on n'a pas fait figurer les transistors MOS reliant les résistances 2R aux lignes horizontales à la masse ou au potentiel E. Supposons que les résistances 8 et 1 sont à E et que les résistances 2 et 4 sont à 0 (ce qui correspond au nombre binaire 1001). Examinons le schéma équivalent à ce réseau de résistances en commençant par la gauche et simplifions en considérant les deux résistances de gauche en les remplaçant par le générateur de Thévenin équivalent |
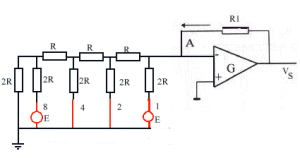

Figure - exemple de la conversion de 1001 et schéma équivalent partiel montrant le principe |
|
En remplaçant on voit que le générateur de Thévenin se retrouve en série avec la première résistance horizontale qui vaut R, laquelle est connectée à la résistance 2R de poids 4 qui est à la masse. On se retrouve avec le même schéma que sur la figure ci-dessus mais en remplaçant E par E/2. Et ainsi de suite on aura 4 fois le même processus et le générateur équivalent à l'ensemble des résistances (en remplaçant le générateur connecté en 1 par un court-circuit) se ramène à une résistance R en série avec E/16. Le même raisonnement en annulant le générateur en 8 permet de montrer que le générateur en 1 est équivalent à R en série avec E/2. |

Figure - schéma équivalent |
|
On additionne donc deux tensions E/2 et E/16 et la sortie de l'ampli Vs = -(R1/R)(E/2 +E/16) = -9ER1/16R ce qui à une constante ER1/16R près est bien proportionnel à 9 dont l'expression binaire est 1001. conversion BCD L'information à convertir peut-être donnée sous forme BCD (si elle provient directement d'une frappe d'un opérateur sur un clavier par ex.). Le principe d'échelle est encore exploitable: chaque échelle, telle celle figurée ci-dessus à 4 bits, pourra exploiter soit les unités, soit les dizaines, soit les centaines, etc. Il suffira de rajouter 1 résistance par décade, l'une valant 9R et les autres valant 8.1R. On obtient alors le schéma suivant qui du point de vue impédance est équivalent à 0.9R. |
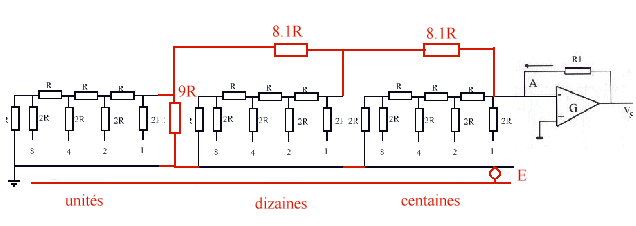
Figure - principe du convertisseur BCD à 3 décades |
|
commutation de courant Plutôt que de commuter des tensions on peut exploiter un principe semblable, mais en commutant les courants. Comme précédemment les résistances 2R seront reliées sur une ligne ou une autre, mais ici ce sera soit la masse, soit l'entrée inverseuse de l'amplificateur (c'est à dire aussi en un point au potentiel zéro si l'amplificateur est supposé idéal). L'intérêt est que le courant circule donc en permanence dans chaque résistance et qu'il est de ce fait invariant, ce qui revient à dire que le temps d'établissement après commutation est maintenant quasi nul. Ce type de convertisseur sera donc plus rapide que son équivalent en tension. Les courants circulant sont dans le rapport 1/2 quand on va de la gauche vers la droite dans les 2R. |

Figure - principe de la commutation de courant |
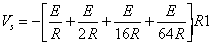 soit effectivement 202 fois le quantum ER1/128R.
soit effectivement 202 fois le quantum ER1/128R.