
( http://energosoyuz.spb.ru/cgi-bin/about.pl?show=news&action=view&num=25 )
ВОПРОСЫ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ РЕЖИМОВ И ГАРМОНИЧЕСКИХ СПЕКТРОВ В СЕТЯХ С РЕЗКОПЕРЕМЕННОЙ И НЕЛИНЕЙНОЙ НАГРУЗКОЙ
При анализе электрических режимов, показателей качества электрической энергии (ПКЭ), а также при разработке мероприятий по оптимизации режимов и условий электромагнитной совместимости необходимо располагать знаниями об изменениях во времени действующих значений токов и напряжений, мощностей, спeектров высших гармоник, коэффициентов несимметрии и т.п. Информацию об указанных параметрах в настоящее время получают с помощью цифровых приборов различного типа, производящих измерения мгновенных значений трехфазных токов и напряжений с частотой дискретизации обычно не менее 6.4 кГц (128 измерений на период промышленной частоты) при последующей обработке сигналов по специальным алгоритмам.
Однако в большинстве
известных приборов, ориентированных на измерение ПКЭ, выводится информация только об усредненных значениях переменных.
Информация о мгновенных переменных, отражающих динамику процессов, пользователю недоступна. Используются, как правило,
интервалы усреднения Туср, регламентированные нормами российского стандарта ГОСТ
Использование таких приборов в электрических сетях с резкопеременной нагрузкой типа дуговых сталеплавильных печей и прокатных станов, где вероятны приращения фазных токов до номинального значения за время 0.1 с и менее, а локальная частота в узле подключения нагрузки вследствие колебаний фазы напряжения может изменяться в пределах ±0.5 Гц, не позволяет получить правдоподобную информацию о процессах.
Для исследования таких режимов в большей степени подходят приборы типа осциллографов-анализаторов, способные измерять мгновенные значения переменных, хранить в памяти результаты их обработки в виде файлов мгновенных значений, а также в виде определенных на интервалах времени, равных периоду промышленной частоты, действующих значений переменных и их спектров. Целесообразность такой концепции построения прибора авторы выдвигали в работе [2]. В «НПФ Энергосоюз» разработан и уже в течение более двух лет успешно эксплуатируется осциллограф-анализатор «НЕВА-ИПЭ», рассчитанный на измерение 32 аналоговых сигналов при частоте дискретизации до 20 кГц. Память прибора допускает непрерывную работу в течение не менее 24 часов.
В приборе заложена неизменность в процессе выполнения конкретных измерений частоты квантования сигналов (постоянство интервала времени измерений). Просмотр осциллографируемых переменных возможен не только после выполнения измерений, но и при их проведении. Причем в темпе процесса дополнительно могут быть рассчитаны и просмотрены на дисплее действующие значения токов и напряжений.
Имеющиеся в приборе два процессора позволяют с некоторым небольшим запаздыванием по отношению к моментам измерений рассчитывать регистрограммы симметричных составляющих, токов и напряжений, фазных и трехфазных мощностей, гармонических спектров.
Гармонический анализ реализован двумя методами — дискретным и быстрым преобразованиями Фурье. При определении гармоник и других параметров используется прямоугольное измерительное окно.
С помощью прибора авторами получены длительные файлы мгновенных значений трехфазных токов i(t) и напряжений u(t) для типовых узлов резкопеременной нагрузки.
Ниже обсуждаются особенности обработок осциллограмм процессов в электрических сетях, питающих резкопеременную и нелинейную нагрузку. Большинство рассматриваемых примеров относится к узлу 35 кВ, к которому подключена дуговая сталеплавильная печь (ДСП), рассчитанная на выплавку стали весом 120 т при мощности печного трансформатора 85 МВА.
О необходимости учета локальных изменений частоты при расчетах эффективных значений, мощностей и частотных спектров
Как известно, некорректное определение частоты процессов может заметно повлиять на точность определения действующих значений сигналов и параметров, характеризующих несинусоидальность и несимметрию процессов.
В приборе «НЕВА-ИПЭ» предусмотрена возможность расчета текущей частоты фазных напряжений несколькими примерно равноценными
способами: по проходам сигнала через ноль, по экстремумам спектральной плотности сигнала, по минимуму среднеквадратического
отклонения сигнала от синусоиды искомой частоты. Разработанные алгоритмы расчета частоты при частоте дискретизации ≥
5 кГц обеспечивают абсолютную погрешность до (
Обратим внимание на то, что вследствие инерционности расчета частоты требуется сдвиг результатов расчета Df в сторону опережения на время DТобр = 0.5?Тобр.
Результирующие погрешности в определении действующих значений и спектров переменных зависят не только
от точности знания текущей частоты первой гармоники сигналов, но и от частоты дискретизации переменных, от ширины окна
обработки сигналов (один или более периодов промышленной частоты), от примененных методов численного интегрирования, от
начальной фазы переменной на окне обработки. Тестовые расчеты показали, что разработанное программное обеспечение прибора
«НЕВА-ИПЭ» при частоте дискретизации fдискр = 10 кГц
позволяет при минимальном окне обработки, равном периоду основной частоты, иметь алгоритмические погрешности определения
действующих значений переменных и уровней основной гармоники не более 0.2 %, а для
При применении окон обработки до 10 периодов основной частоты эти погрешности уменьшаются в 2 — 4 раза.
Еще раз подчеркнем, что указанные данные о точности расчетов справедливы
при слежении за частотой первой гармоники. Если учет частоты не производится и она отклоняется до значений ±0.5 Гц, то
погрешности в определении основной,
О том, что большие локальные изменения частоты возможны, свидетельствуют, например, приведенные на рис. 1а измерения частоты в узле 35 кВ питания ДСП. Здесь использовались скользящие интервалы обработки Tобр = 0.04 с.

Рис. 1. Частота напряжения фазы «А» в узле питания ДСП, определенная методом скользящего среднего на интервалах обработки длительностью 0.04(а), 0.2 и 3 секунды (б).
Увеличение интервала Tобр при определении частоты до значения Tобр = 0.2 с в 5 раз уменьшает фиксируемые колебания частоты, а при Tобр = 3 с колебания частоты практически незаметны (рис. 1б). Во избежании появления дополнительных погрешностей в определении спектров переменных желательно использовать информацию о частоте, определенной на минимальных интервалах обработки.
Заметим, что согласно измерениям локальные изменения частоты в узлах питания 10 кВ мощных реверсивных прокатных станов могут достигать пределов ±0.2 Гц.
Об определении действующих значений переменных и гармоник в сетях с быстроизменяющейся нелинейной нагрузкой
Для оценок динамики изменения действующих значений переменных в сетях с резкопеременной нагрузкой следует проводить расчеты, как минимум, на каждом чередующемся периоде основной частоты. При этом в соответствии с данными предыдущего подраздела для повышения точности желательно предварительно производить расчетную оценку текущей частоты, и, соответственно, длительности периода Т, на котором осуществляется численное интегрирование по формуле:
 ,
,
где индекс i отвечает измерениям, равноотстоящим на шаге дискретизации Δt = 1/fдискр, N — число точек измерений, укладывающихся на периоде Т, ΔХэфф — добавка, учитывающая то обстоятельство, что, как правило, N?Δt < Т. Исследования показали, что при частоте дискретизации ≥ 10 кГц добавкой ΔХэфф можно пренебречь.
Как известно, при нестабильных режимах нелинейной нагрузки в спектрах тока и напряжения кроме кратных основной частоте гармоник содержатся также промежуточные гармоники с частотами выше и ниже промышленной частоты 50 Гц.
Для наблюдения за этими гармониками окно (англ. window) разложения сигнала в ряд Фурье Тw следует принимать повышенным по сравнению с периодом основной частоты. Если при Тw = 0.02 c возможно определение только целочисленных гармоник, кратных основной частоте, то при Тw = k?0.02 c можно наблюдать все промежуточные гармоники с частотами 50/k Гц.
В российском ГОСТ 13109-97 [1] для нестабильных режимов рекомендуется применять окна Тw = (0.08 ÷ 0.32) с или k = 4 ÷ 16 (Приложение Е). Однако этот ГОСТ и следующие ему методики измерений ориентированы только на целочисленные гармоники. Не даются пояснения того факта, что расчетные величины гармоник, в том числе и кратных основной частоте, принципиально зависят от выбора окна Тw.
Проиллюстрируем сказанное на примере статистического анализа действующих значений гармоник тока ДСП в режиме расплавления на интервале времени 20 секунд. Гармоники рассчитывались с применением двух прямоугольных скользящих окон 0.02 с и 0.2 с, смещающихся через период промышленной частоты (итого обрабатывались массивы, содержащие по 1000 расчетных значений гармоник). На рис. 2 представлены спектральные составляющие для гармоник в диапазоне 0 ÷ 6. При малом окне 0.02 с значения целочисленных гармоник (кроме основной) в два и более раза превышают их расчетные значения, определенные при окне 0.2 с. Причина этого состоит в том, что в амплитуде целочисленных гармоник при Тw = 0.02 c отражена энергия, приходящаяся на ненаблюдаемые в данном случае промежуточные гармоники.
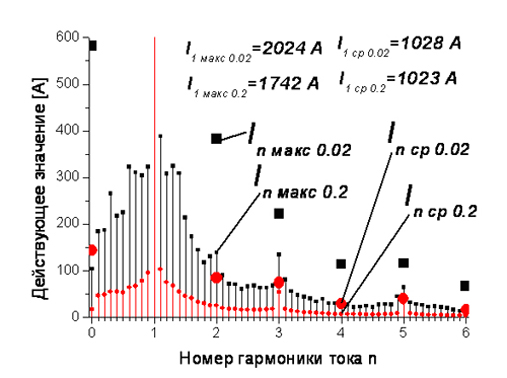
Рис. 2. Максимальные и усредненные действующие значения спектральных составляющих тока фазы «А» на стороне 35 кВ ДСП, полученные на интервале наблюдения 20 секунд, с окнами разложения 0.02 с (большие маркеры) и 0.2 с (маленькие маркеры).
Аналогичная ситуация наблюдалась и при анализе напряжений в сетях питания ДСП. Причем
вследствие известного эффекта возрастания на высших гармониках сопротивления системы, имеющего преимущественно индуктивный
характер, здесь в рассматриваемом диапазоне частот 0 ÷ 300 Гц все промежуточные гармоники соизмеримы между собой
и с целочисленными гармониками.
В стандарте МЭК IEC 61000-4-7 [3] приводится понятие о гармонических
группах, содержащих кроме целочисленных гармоник также и ближайшие к ним промежуточные гармоники. В этом стандарте
рекомендуется для применения окно Тw = 0.2 c, и при этом становится доступной информация о девяти спектральных
промежуточных линиях между соседними целочисленными гармониками. В этом случае формула эквивалентирования пяти
спектральных линий тока перед и после целочисленной гармоники n имеет вид:
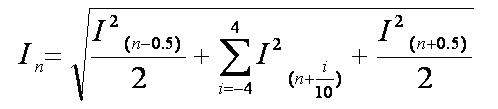 ,
,
где весовой коэффициент 0.5 в первом и третьем членах учитывает вклад этих спектральных линий в обе равноудаленные целочисленные гармоники.
Нетрудно убедиться, что использование данных о промежуточных гармониках из рис. 2. для расчета эквивалентных целочисленных гармоник, отвечающих разложению при Tw = 0.02 c, полностью подтверждает справедливость приведенный формулы.
К сожалению, пользователям отечественных приборов для измерения ПКЭ, ориентированным на требования ГОСТ 13109-97 [1], доступна информация только о целочисленных гармониках. Поскольку ширина примененного в приборах окна разложения обычно неизвестна, то в сетях с быстроизменяющейся нагрузкой информация даже о величинах целочисленных гармоник является непредставительной, не точно характеризующей нелинейные искажения.
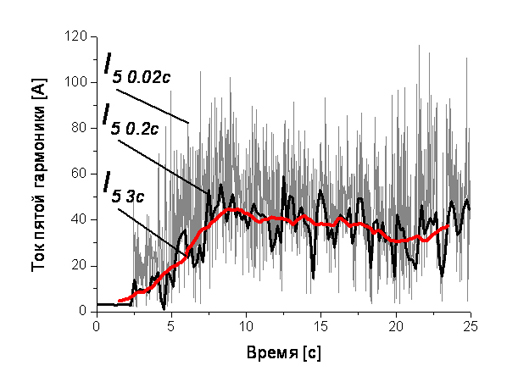
Рис. 3. Действующие значения тока пятой гармоники фазы «А» на начальном этапе работы ДСП, определенные на скользящих интервалах обработки длительностью 0.02 и 3 секунды.
К вышесказанному добавим, что применяемые в приборах ПКЭ дополнительные усреднения результатов расчета гармоник на трехсекундном интервале (требования стандарта [1]) тем более не позволяют проследить динамику изменений гармоник. Это видно из построений на рис. 3, где на начальном этапе плавки ДСП показано, как изменяется пятая гармоника при окнах измерений 0.02 с, 0.2 с, а также при последующем трехсекундном усреднении расчетов со скользящим интервалом 0.2 с. О причинах отличия гармоник, рассчитанных при использовании окна 0.02 с и окна из 10 периодов говорилось выше: пониженные значения гармоники при большом окне разложения учитывают значительное перераспределение энергии целочисленной гармоники в промежуточные гармоники.
Следует также подчеркнуть, что при применении окон разложения (усреднения), больших одного периода промышленной частоты, получаемые расчетные данные о действующих значениях переменных относятся к моменту времени, соответствующему середине окна измерений. Это учтено при построениях кривых на рис. 3 за счет их соответствующего сдвига.
Выводы
1. Показаны преимущества использования цифровых осциллографов-анализаторов с гибким программным обеспечением для исследования режимов систем электроснабжения с резкопеременной и нелинейной нагрузкой. Приведены примеры специфических обработок осциллограмм для получения текущих значений частоты в узлах с резкопеременной активной нагрузкой и оценок динамики изменения действующих значений переменных и их высших гармоник.
2. Для корректного измерения действующих значений переменных в резкопеременных электрических режимах желательно применять измерительное окно, отвечающее предварительно рассчитанному периоду основной частоты для исследуемых моментов времени.
3. Расчетные значения гармоник переменных в сетях с резкоизменяющейся нагрузкой принципиально зависят от величины временного окна, выбранного при разложении сигналов в ряд Фурье. При ширине окна, большем одного периода основной частоты, фиксируется спектр сигналов с промежуточными гармониками, причем в этом спектре амплитуды целочисленных гармоник заметно уменьшаются.
4. Использование приборов для измерения ПКЭ в сетях с нестабильной нелинейной нагрузкой в настоящее время проблематично по причинам заложенных в них алгоритмов усреднений результатов расчетов и ориентацией на расчет только целочисленных гармоник. Целесообразно внесение соответствующих изменений программное обеспечение этих приборов.
ЛИТЕРАТУРА
1. ГОСТ
2. Kuchumov L., Kouznetsov
A., Sapunov M. «Processes oscilloscoping as a necessary component for electric power quality disturbances analysis in
industrial power supply systems». Technische Universität Ilmenau (Deutschland). 48. Internationales Wissenschaftliches
Kolloquium
3. IEC
Леонид Кучумов, проф. СПбГПУ,
Антон Кузнецов, доцент СПбГПУ,
Михаил Сапунов, инженер ЗАО
«НПФ «Энергосоюз»