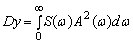 (1)
(1)
( http://www.masters.donntu.ru/t2005/eltf/mesheryakova/library/book4.htm )
УДК 621.3.05:519.2
Линейная фильтрация случайных электроэнергетических процессов. Метод парциальных реакций
Черникова Л. В. Донецкий государственный технический университет
При оценке воздействий помехи x(t) на электроприемники необходимо учитывать реакцию y(t) электроприемника на помеху. Поэтому в математических моделях электромагнитной совместимости (ЭМС) электроприемников имеется линейный фильтр, который моделирует реакцию [1]. Фильтр описывается передаточной функцией W (p) в виде отношения многочленов f(p) и z(p) степеней m и n при m < n. Например, фильтр фликерметра Международной электротехнической комиссии имеет m = 2 и n = 4.
При стационарных случайных помехах задача заключается в определении среднего значения yc и дисперсии Dy в стационарном состоянии по среднему значению xc и спектральной плотности S(w) или корреляционной функции k(t) (КФ) помехи. Амплитудно-частотная А(w) и фазочастотная j(w) функции (АЧФ и ФЧФ) фильтра определяются по передаточной функции известными методами.
Вычисление дисперсии по общей формуле
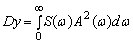 (1)
(1)
с применением теоремы о вычетах не встречает принципиальных затруднений, но сопряжено с громоздкими выкладками. Кроме того, для каждой системы, имеющей другую передаточную функцию, необходимо заново выполнять все выкладки. В связи с этим возникает необходимость в разработке унифицированного метода решения задач линейной фильтрации, что является целью статьи.
Предлагаемый метод «парциальных реакций» основан на разложении передаточной функции W(p) на многочлены первого порядка. При этом возможны два типа задачи: во-первых, найти решение для различных видов помех и, во-вторых, считать, что во всех случаях входным процессом является белый шум x(t).
Рассмотрим первый тип задачи. Пусть р1, р2, ... , рn – простые корни характеристического уравнения z(p) = 0. Известно, что отношение многочленов можно представить в виде суммы дробей:
 (2)
(2)
с коэффициентами

Если 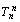 – множитель при
– множитель при 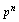 в знаменателе, то
в знаменателе, то
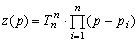
Обозначим через
 ;
;
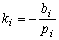 (3)
(3)
В результате получим выражение
 ,
,
из которого следует, что фильтр (рис. 1,а) представлен в виде параллельно включенных инерционных (апериодических) звеньев первого порядка (рис. 1,б) с постоянными времени И и коэффициентами передачи k. Параметры звеньев могут быть комплексными величинами. Таким образом, задача вычисления характеристик «парциальных» реакции свелась к определению характеристик реакций инерционных звеньев.
В стационарном состоянии среднее значение
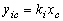 ,
,
поэтому

Рисунок 1 – Структурная схема фильтра
(4)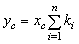
Для инерционного звена АЧФ
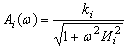 (5)
(5)
в связи с чем, дисперсия реакции i-го звена составит
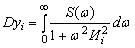 (6)
(6)
Впервые метод разложения линейного фильтра на отдельные инерционные звенья был предложен в [2]. Принципиальным отличием случайных «парциальных» реакций от периодических является их взаимная зависимость, обусловленная тем, что на входы инерционных звеньев поступает один и тот же процесс x(t). Это обстоятельство необходимо учитывать при определении дисперсии суммы реакций. Для этой цели помимо дисперсий (6) найдем взаимные корреляционные моменты между попарно взятыми реакциями i-го и r-го звеньев. Учитывая, что ФЧФ инерционного звена дается выражением
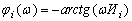
общую формулу

теории случайных процессов представим в виде
 (7)
(7)
Тогда искомая дисперсия составит
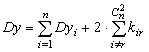 (8)
(8)
Несмотря на увеличение количества слагаемых, вычисления по этой формуле проще, так как достаточно один раз вычислить Dyi и kir для заданной спектральной плотности или КФ.
Например, для помех с экспоненциальной КФ
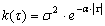 (9)
(9)
когда
 (10)
(10)
при
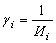 получим
получим
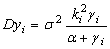 ; (11)
; (11)
 , (12)
, (12)
где s – стандарт;
a – величина, обратная времени корреляции;
Для помех с экспоненциально-косинусоидальной КФ
 , (13)
, (13)
где a и w0 – параметры КФ, при
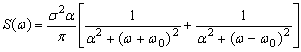 (14)
(14)
получим
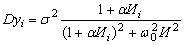 ; (15)
; (15)
 . (16)
. (16)
Полученные формулы унифицируют расчеты дисперсий при любой сложности фильтра и заданной КФ.
Перейдем к рассмотрению второго типа задачи. Полной унификации можно достичь, основываясь на фундаментальном положении о том, что наблюдаемые на практике стационарные случайные процессы являются результатом прохождения белого шума x(t) через гипотетическую линейную систему [3]. Передаточная функция G(p) такой системы определяется спектральной плотностью (КФ) помехи (рис. 2).

Рисунок 2 – Структурная схема фильтра с получением входного процесса путем преобразования белого шума
Использование белого шума значительно упрощает расчеты, поскольку его спектральная плотность постоянна
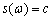 (17)
(17)
и КФ имеет вид
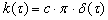 (18)
(18)
где с – постоянная величина;
d(t) – дельта-функция.
Найдем передаточную функцию G(p) для помехи с экспоненциальной КФ (9). Из формулы (10) следует, что искомая система представляет собой инерционное звено с постоянной времени Иx = 1/a [4]:
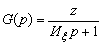 (19)
(19)
Коэффициент передачи z звена находится из условия воспроизведения заданной спектральной плотности, которая дает соотношение
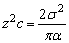 (20)
(20)
Отсюда следует, что можно принимать различные значения c или z с учетом выполнения условия (20). Для устранения неопределенности и унификации формул примем с = 1. В этом случае коэффициент
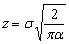 (21)
(21)
однозначно выражается через заданные параметры s и a, но имеет размерность, что не существенно.
Аналогичным образом процесс с экспоненциально-косинусоидальной КФ (13) можно получить, пропустив белый шум через систему, состоящую из последовательно включенных форсирующего и колебательного звеньев:
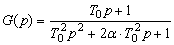 , (22)
, (22)
где  .
.
Полученная эквивалентная передаточная функция  используется для расчета по методу «парциальных реакций».
используется для расчета по методу «парциальных реакций».
Найдем характеристики реакции на выходе i-го инерционного звена, когда на вход фильтра поступает белый шум. Дисперсия определяется по известной формуле [5].
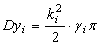 ; (23)
; (23)
В соответствии с общей формулой (7) получим
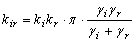 , (24)
, (24)
где учтено, что с = 1.
Проиллюстрируем применение предлагаемого метода на примере, решение которого известно. Рассмотрим задачу оценки погрешности измерения случайного процесса с экспоненциальной КФ (9) измерительным прибором, имеющим передаточную функцию
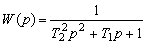 , (25)
, (25)
где Т1, Т2 – постоянные времени прибора.
Решение этой задачи известно и приведено на с. 131 [5]. Динамическая погрешность измерения определяется дисперсией Dy измеренного процесса. В задаче первого типа (символ ~) входной процесс остается неизменным. Поскольку в данном случае n = 2, то прибор моделируется двумя инерционными звеньями (рис. 3, а). Полученные по формулам (3), (6), (7), (8) выражения, приведены в табл. 1. В задаче второго типа добавляется инерционное звено с постоянной времени Иd (рис. 3, б). Существенно, что постоянные времени остальных звеньев такие же как и в предыдущем случае: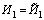 ,
,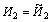 , но коэффициенты передачи звеньев k будут другими (табл. 1).
, но коэффициенты передачи звеньев k будут другими (табл. 1).

Рисунок 3 – Эквивалентные структурные схемы фильтра для расчета дисперсии на выходе измерительного прибора
Таблица 1 – Расчет дисперсии реакции на выходе измерительного прибора
| Наименование параметра | Задача первого типа(рис.3,а) | Задача второго типа(рис.3,б) |
| Передаточная функция системы | 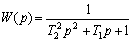 |
 |
| Корни знаменателя передаточной функции |  |
  |
| Постоянные времени инерционных звеньев |  |
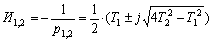  |
| Коэффициенты передачи инерционных звеньев |  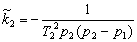 |
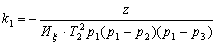  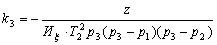 |
| Дисперсии на выходе инерционных звеньев | 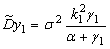 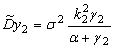 |
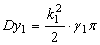 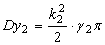 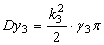 |
| Взаимные корреляционные моменты | 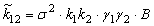 , где , где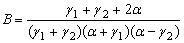 |
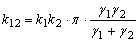 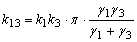  |
| Дисперсия измеренного процесса | 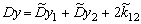 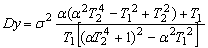 |
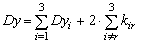  |
Как и следовало ожидать, дисперсия измеренного процесса после соответствующих преобразований в обоих случаях получается одинаковой и совпадает с формулой в [5].Реализация метода "парциальных реакций" на ПЭВМ сводится к расчетам по конечным аналитическим выражениям.Это позволяет избежать погрешности, возникающей при численном интегрировании с бесконечным верхним пределом согласно [1].
Вывод.Представление линейных систем в виде параллельно включенных инерционных звеньев позволяет унифицировать и упростить решение задач линейной фильтрации электроэнергетических случайных процессов.
Литература
1. Электромагнитная совместимость электроприемников промышленных предприятий / Под ред. А. К. Шидловского. – Киев: Наукова думка, 1992. – 236 с.
2. Абу Сиам Сами. Методы расчёта динамических показателей электромагнитной совместимости элек-трооборудования с периодической нагрузкой и систем электроснабжения. –Диссертация на соискание уч. сте-пени, канд. техн. наук. – г. Донецк, 1992, – 202с.
3. Прохоров Ю. В., Розанов Ю. А. Теория вероятностей: Основные понятия. Предельные теоремы. Слу-чайные процессы. – М.: Наука, 1967. – 496 с.
4. Куренный Э. Г., Дмитриева Е. Н., Петрушечкина Л. М., Пушная И. В. Имитация графиков электриче-ской нагрузки преобразованием белого шума // Техническая электродинамика. – 1986. – № 6. – С. 56 – 62.
5. Шидловский А. К., Куренный Э. Г. Введение в статистическую динамику систем электроснабжения. - Киев: Наукова думка, 1984. - 272 с.
Эта статья опубликована в сборнике научных трудов ДонГТУ. Серия: Электротехника и энергетика, выпуск 4. - Донецк: ДонГТУ, 1999. - С. 217 - 220.