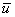 (ресурсов оптимизации) из допустимой области их определения
(ресурсов оптимизации) из допустимой области их определения 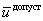 , которые обеспечивают экстремальную (наибольшую или наименьшую) величину критерия оптимальности.
, которые обеспечивают экстремальную (наибольшую или наименьшую) величину критерия оптимальности.| ДонНТУ | Портал магистров | Биография | Автореферат | Библиотека | Ссылки | Отчет о поиске |
Оптимизация – это процедура нахождения наилучших условий проведения химического процесса.
Задача оптимизации рассматривается как математическая задача поиска экстремального значения функции многих переменных.
Формулировка задачи оптимизации для многих переменных:
Необходимо найти такие значения оптимизирующих переменных 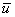 (ресурсов оптимизации) из допустимой области их определения
(ресурсов оптимизации) из допустимой области их определения 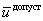 , которые обеспечивают экстремальную (наибольшую или наименьшую) величину критерия оптимальности.
, которые обеспечивают экстремальную (наибольшую или наименьшую) величину критерия оптимальности.
В результате задачу оптимизации можно представитьвследующим виде:
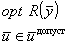
Связь выходных переменных 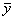 с другими переменными задаётся отображением с физико-химическим оператором:
с другими переменными задаётся отображением с физико-химическим оператором:
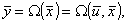
где входные переменные 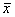 , определяющие состояние моделируемого объекта, разбиваются на две группы переменных:
, определяющие состояние моделируемого объекта, разбиваются на две группы переменных: 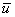 - оптимизирующие
переменные, которые можно контролировать и регулировать и
- оптимизирующие
переменные, которые можно контролировать и регулировать и 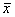 - контролируемые, но не регулируемые переменные (не могут использоваться как ресурсы оптимизации).
- контролируемые, но не регулируемые переменные (не могут использоваться как ресурсы оптимизации).
В результате задача оптимизации представляется в следующем виде:

На оптимизирующие переменные 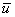 и выходные переменные
и выходные переменные 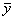 могут накладываться ограничения (возможность изменения переменных только в определённых пределах).
могут накладываться ограничения (возможность изменения переменных только в определённых пределах).
На практике выходные переменные 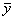 при решении задачи оптимизации определяются либо из экспериментальных данных – экспериментально-статистический метод оптимизации, либо с помощью математических моделей процессов – численный метод оптимизации.
при решении задачи оптимизации определяются либо из экспериментальных данных – экспериментально-статистический метод оптимизации, либо с помощью математических моделей процессов – численный метод оптимизации.
Математические модели в этом случае формализуются с помощью отображения с функциональным оператором:
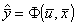
Замена вектора выходных переменных 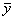 на вектор оценок выходных переменных
на вектор оценок выходных переменных 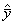 , полученных при расчёте по математической, модели позволяет рассматривать задачу оптимизации как математическую задачу поиска экстремума функции многих переменных на компьютере.
, полученных при расчёте по математической, модели позволяет рассматривать задачу оптимизации как математическую задачу поиска экстремума функции многих переменных на компьютере.
Задача: определение максимума функции R = R( u )
Результат решения: 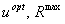 .
.
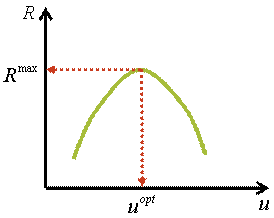
Пример:
Для последовательной реакции A → P → S , изменение концентраций компонентов которой представлено ниже на рисунке, можно сформулировать следующую задачу оптимизации: найти оптимальное время реакции ( topt ), при котором концентрация промежуточного продуктаР будет максимальной.
Для решения задачи оптимизации необходимо:
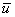 );
);Критерий оптимальности является количественной характеристикой качества функционирования процесса.
Различают физико-химические (концентрация целевого продукта, примеси, выход продукта) и экономические (себестоимость, прибыль, рентабельность) критерии оптимальности.
Значение критерия оптимальности зависит от выходной переменной, рассчитываемой с помощью математической модели (численный метод оптимизации). Предполагается, что при оптимизации применяются математические модели, для которых предварительно решена задача идентификации. Соответственно коэффициенты модели не показаны в равенстве:
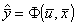
Если адекватную математическую модель процесса построить не удаётся, то значение выходной переменной 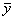 в уравнении:
в уравнении:
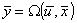
определяется из опытов (экспериментально-статистический метод оптимизации). В этом случае реализуется оптимальная стратегия проведения эксперимента (активный эксперимент).
Требования к критерию оптимальности:
Таким образом, при выборе критерия оптимальности необходимо стремиться к тому, чтобы его функция была унимодальной с одним экстремумом и не содержала точек разрыва.
Эти переменные выбираются из числа входных переменных процесса.
Если в число оптимизирующих переменных включены конструктивные характеристики процесса (размеры, типы конструкций и т.п.), то решается задача оптимального проектирования.
Если в число оптимизирующих переменных не включены конструктивные характеристики процесса (размеры, типы конструкций и т.п.), то решается задача оптимального управления. В этом случае оптимизирующие переменные называются управляющимипеременными и поиск их оптимальных значений осуществляется с целью определения наилучших режимных параметров действующих процессов.
Для решения задачи оптимизации численным методом на компьютере необходимо располагать:
Обобщённая блок-схема оптимизации численным методом:
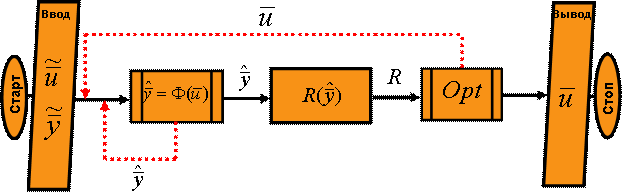
Эти методы применяются, когда построить математическую модель невозможно. Известны лишь факторы 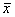 (оптимизирующие переменные) и выходная переменная y (критерий оптимальности), значение которой определяется опытным путём.
(оптимизирующие переменные) и выходная переменная y (критерий оптимальности), значение которой определяется опытным путём.
Формулировка задачи оптимизации :
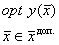
Так как выходная переменная определяется из опытных данных, для поиска её экстремальных значений необходимо реализовать оптимальную стратегию экспериментирования.
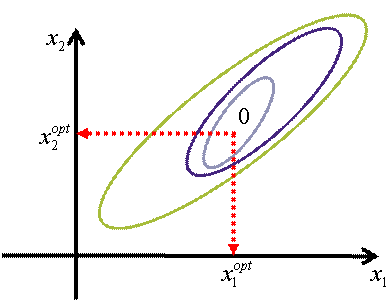
Функция критерия оптимальности y=y(x1, x2,..., xm) в этом случае может быть представлена в виде поверхности отклика, одинаковые значения которой для двух факторов ( x1, x2 ) изображаются линиями постоянного уровня ( y = const ). Эти линии являются проекциями сечений поверхности отклика на плоскость факторов. Искомая экстремальная точка поверхности отклика соответствует точке «0».
В этом случае используется «шаговый» метод движения по поверхности отклика с целью определения её экстремального значения.
При этом выделяются два этапа планирования эксперимента:
Движение к экстремуму осуществляется по направлению градиента (антиградиента) функции отклика у.
Вектор градиента определяет направление наискорейшего возрастания функции идля
y=y(x1, x2,..., xm) равен:
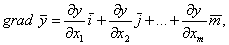 где
где
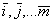 - единичные векторы в направлении осей координат;
- единичные векторы в направлении осей координат;
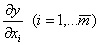 - проекции вектора градиента на оси координат
- проекции вектора градиента на оси координат 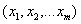
Для m = 2 движение методом крутого восхождения можно представить:
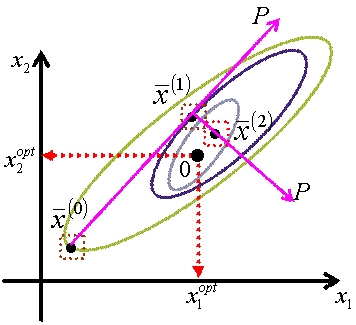
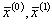 - центры планов эксперимента первого порядка (ПФЭ)
- центры планов эксперимента первого порядка (ПФЭ)
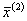 - центр плана эксперимента второго порядка (ОЦКП)
- центр плана эксперимента второго порядка (ОЦКП)
Последовательные координаты поиска экстремума в факторном пространстве определяются по формуле:
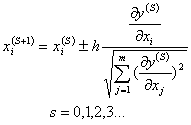 , где
, где
h - задаваемый фактор шага по направлению вектора-градиента;
s - номер точки экспериментирования;
Величина y здесь определяется из уравнения регрессии, которое является линейным относительно факторов и коэффициентов:
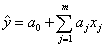
Это уравнение используется для локального описания поверхности отклика в областях, далёких от её экстремального значения.
Ограниченная область факторного пространства, где справедливо это уравнение регрессии, задаётся центром области 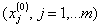 – центром плана эксперимента:
– центром плана эксперимента:
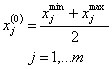
и интервалом (точнее, полуинтервалом) варьирования факторов:
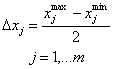
Для локальной области факторного пространства уравнение регрессии записывается с кодированными факторами:
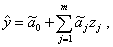 где
где
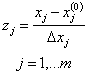
В результате минимальному значению фактора соответствует zj = -1, максимальному - zj = 1, а центру плана эксперимента – точка с координатами zj = 0, j = 1, …m
Коэффициенты уравнения регрессии с кодированными факторами 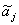 отличаются от коэффициентов уравнения регрессии с натуральными значениями факторов xj и определяются из полного факторного эксперимента (ПФЭ), проведённого в рассматриваемой ограниченной области.
отличаются от коэффициентов уравнения регрессии с натуральными значениями факторов xj и определяются из полного факторного эксперимента (ПФЭ), проведённого в рассматриваемой ограниченной области.
Одним из таких свойств является свойство ротатабельности, которое характеризует равную предсказательную способность уравнения регрессии с кодированными факторами на одинаковом расстоянии от центра плана.
Для характеристики предсказательной способности уравнения регрессии используется оценка дисперсии выходной переменной 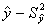 , которая из-за статистической независимости коэффициентов
, которая из-за статистической независимости коэффициентов 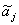 и их одинаковой дисперсии в случае ПФЭ определяется по формуле:
и их одинаковой дисперсии в случае ПФЭ определяется по формуле:
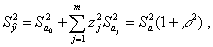 где
где
Sa2 - одинаковая для всех коэффициентов оценка дисперсии 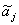 ,
,
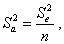 где
где
n - число опытов ПФЭ
Se2 - дисперсия воспроизводимости выходной переменной у , определяемая по параллельным опытам
ρ2 - квадрат расстояния из центра плана до рассматриваемой точки факторного пространства:
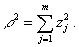
Величина, обратная 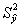 , принимается за меру точности уравнения регрессии.
, принимается за меру точности уравнения регрессии.
Точность уравнениядля 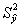 убывает пропорциональноквадрату радиуса сферы ρ2 и одинакова для всех эквидистантных точек.
убывает пропорциональноквадрату радиуса сферы ρ2 и одинакова для всех эквидистантных точек.
Поэтому в факторном пространстве нельзя выделить ни одно предпочтительное направление, и вектор градиента ( 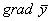 )не хуже, в смысле предсказания величины выходной переменной у, чем любое другое направление.
)не хуже, в смысле предсказания величины выходной переменной у, чем любое другое направление.
Однако вектор-градиент (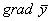 ) характеризует направление наискорейшего возрастания функции у и в этом смысле движение по нему является наиболее предпочтительным.
) характеризует направление наискорейшего возрастания функции у и в этом смысле движение по нему является наиболее предпочтительным.
Для определения координат вектора-градиента ( 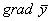 ) используется адекватное уравнение регрессии, полученное по результатам ПФЭ:
) используется адекватное уравнение регрессии, полученное по результатам ПФЭ:
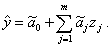
Задаётся фактор шага h, и из центра плана ПФЭ (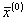 - начальное приближение) выполняется шаг по градиенту в сторону экстремального значения функции отклика, определяются координаты нового центра плана в факторном пространстве -
- начальное приближение) выполняется шаг по градиенту в сторону экстремального значения функции отклика, определяются координаты нового центра плана в факторном пространстве - 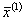 .
.
Здесь снова проводится ПФЭ, обрабатываются его результаты, вычисляется новое направление вектора-градиента:
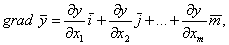
покоторому выполняется шаг
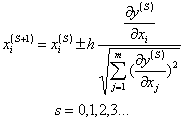
в сторону экстремума. Процедура последовательного экспериментирования продолжается до тех пор, пока не будетдостигнута область, близкая к экстремальному значению функции отклика.
Близость почти стационарной области может быть установлена с помощью t – критерия Стьюдента путём оценки значимости
различия между экспериментальными 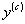 и расчётными
и расчётными 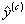 величинами в центре плана.
величинами в центре плана.
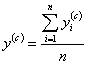
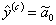
Условие близости экстремума функции отклика имеет вид:
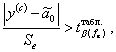 где
где
fe = k – 1 - число степеней свободы
k - число параллельных опытов
β - заданная доверительная вероятность (обычно 0,95)
Для определения (уточнения) оптимальных величин факторов, обеспечивающих экстремальное значение выходной переменной у, решается система уравнений, которая вытекает из необходимого условия экстремума функции многих переменных:
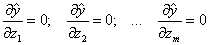
В данном случае также удобнее пользоваться кодированными факторами zj.
Для описания области, близкой к экстремуму, можно использовать уравнение второго порядка с двойными взаимодействиями факторов:
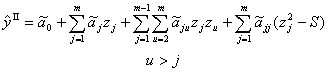
Введение величины S обеспечивает ортогональность матрицы эксперимента, который проводится с целью определения коэффициентов ( 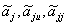 ) этой модели.
) этой модели.
Для вычисления коэффициентов уравнениядля 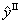 реализуется ОЦКП эксперимента в почти стационарной области.
реализуется ОЦКП эксперимента в почти стационарной области.
Результатрешения задачи уточнения положения экстремума нельзя считать удачным, если не выполняется условие:
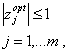
т.к. уравнение регрессии справедливо только в диапазоне кодированных факторов
(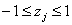 ), где был поставлен эксперимент.
), где был поставлен эксперимент.
При невыполнении этого условия рекомендуется снова реализовать ОЦКП эксперимента с новым центром плана, в частности в точке 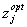 .
.
Эту процедуру последовательного экспериментирования в окрестности экстремума рекомендуется продолжать до тех пор, пока условие приведённого выше неравенства не выполнится.
| ДонНТУ | Портал магистров | Биография | Автореферат | Библиотека | Ссылки | Отчет о поиске |