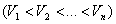 . Верхний предел регулирования
. Верхний предел регулирования  выбирается из первого условия, а остальные ступени
выбирается из первого условия, а остальные ступени 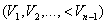 — из второго условия. Известно, что максимальная производительность конвейера А линейно зависит от его скорости:
— из второго условия. Известно, что максимальная производительность конвейера А линейно зависит от его скорости:
На главную
Реферат | Библиотека | Ссылки |
Отчет о поиске
"Горные машины и автоматика", 1969, №2, стр. 52 - 54.
Грузопоток угля, поступающий на конвейер при работе выемочной машины, неравномерен. Регулирование скорости конвейера в зависимости от грузопотока позволяет уменьшить пробег грузонесущего органа, его износ, а также расход электроэнергии. Параметры регулирования скорости конвейера рекомендуется принимать из условий: 1) обеспечения экономически целесообразной производительности выемочной машины и 2) минимальной средней скорости движения грузонесущего органа.
При ступенчатом регулировании скорости конвейера требуется выбрать ступени регулирования 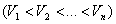 . Верхний предел регулирования
. Верхний предел регулирования  выбирается из первого условия, а остальные ступени
выбирается из первого условия, а остальные ступени 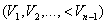 — из второго условия. Известно, что максимальная производительность конвейера А линейно зависит от его скорости:
— из второго условия. Известно, что максимальная производительность конвейера А линейно зависит от его скорости:
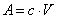  
| (1) |
где
А - максимальная производительность конвейера, т/ч;
c - безразмерный коэффициент;
V - скорость конвейера, м/с.
Скорость 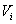 следует включать тогда, когда грузопоток угля Q, поступающий на конвейер, находится в интервале
следует включать тогда, когда грузопоток угля Q, поступающий на конвейер, находится в интервале 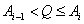
Грузопоток угля при работе выемочной машины является случайной величиной, поэтому работа конвейера со скоростью 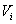 - случайное событие.
- случайное событие.
Средняя скорость грузонесущего органаконвейера (математическое ожидание) определяется по формуле:

| (2) |
где F(x) - функция распределения грузопотока угля, поступившего на конвейерпри работе выемочной машины.
Следует выбрать такие значения 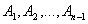 , которые минимизируют среднюю скорость MV. Если распределение грузопотока Q является непрерывным, т. е. существует производная F`(x) = f(x) при x > 0, то оптимальные значения
, которые минимизируют среднюю скорость MV. Если распределение грузопотока Q является непрерывным, т. е. существует производная F`(x) = f(x) при x > 0, то оптимальные значения 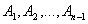 должны удовлетворять системе уравнений:
должны удовлетворять системе уравнений:
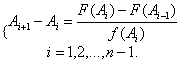
| (3) |
Можно считать, что F(x) - функция, а f(x) - плотность нормального распределения с математическим ожиданием  и дисперсией
и дисперсией  . Путем следующей замены переменных и функций:
. Путем следующей замены переменных и функций:
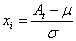
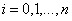

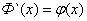
| (4) |
получим окончательно:
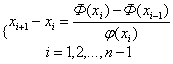
| (5) |
При фиксированном значении  система (5) имеет единственное решение
система (5) имеет единственное решение 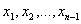 , которое минимизирует МV. Это решение легче всего определеяется графически. Исходя из первого уравнения строится график функции
, которое минимизирует МV. Это решение легче всего определеяется графически. Исходя из первого уравнения строится график функции 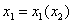 , исходя из второго уравнения и данного графика - график функции
, исходя из второго уравнения и данного графика - график функции 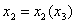 и т. д.
Функции берутся по таблицам нормального распределения. Корни ситемы (5)
и т. д.
Функции берутся по таблицам нормального распределения. Корни ситемы (5) 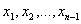 при заданном значении
при заданном значении  определяются по графикам в обратном порядке.
определяются по графикам в обратном порядке.
По формулам (4) определяются соответствующие значения 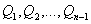 .
.
