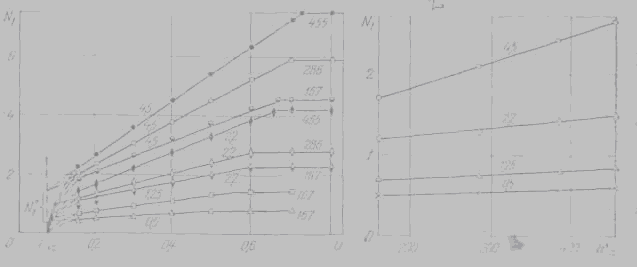
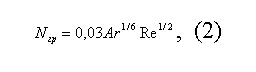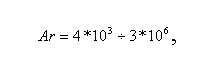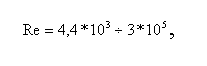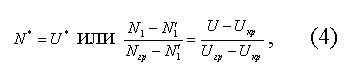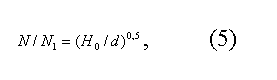Рис 1 - Влияние влажности материала U кг влаги/кг сухого материала на интенсивность срыва N1 для слоя толщиной в одну частицу. Цифры у кривых справа – скорость воздуха на выходе из сопла Wс м/сек ; цифры у кривых – размеры частиц d, мм.
Рис 2 - Зависимость числа срыва N1 от скорости газа Wс , м/сек на выходе из сопла при влажности материала U=0,2 кг влаги/кг сухого вещества. Цифры у кривых – размеры частиц, мм.
В настоящее время нам не удалось в полной мере выделить собственно процесс механического срыва влаги с поверхности частиц. Поэтому при обработке экспериментальных данных принимали, что в результате конвективного массообмена воздух полностью насыщается влагой до значения Xр, а избыток ее Х=Xк/Xр относили за счет срыва влаги. Относительное избыточное количество удаленной влаги N= X/Xр, именуемое ниже «числом срыва», представляли в зависимости от перечисленных выше параметров процесса.
Влияние влажности материала на число срыва N1 для слоя толщиной в одну частицу (Ho = d) показано на рис. 1. Нулевому значению числа срыва физически соответствует Uкр= 0,07 кг влаги/кг сухого вещества. С ростом влажности U сверх Uкр число срыва N1 растет вначале быстро (штрих на рисунке), а затем линейно (сплошные линии) до определен¬ного граничного значения Uгр, за пределами которого N1, сохраняет по¬стоянное (граничное) значение Nгр. Подчеркнем, что для более крупных частиц кривые N1=N1(U) располагаются выше. Из рис. 1 также следу¬ет, что число срыва , N1 растет с увеличением скорости газа Wc, причем в исследованном диапазоне скоростей этот рост близок к линейному (рис. 2). Наконец, на интенсивность срыва влаги влияет высота слоя (рис. 3): крайние левые точки отвечают величинам N1; первоначально N возрас¬тает с повышением Ho. однако при достижении некоторых предельных значений Hкр влияние Ho вырождается.
Возрастание интенсивности срыва (N1, N и Nгр,) с ростом размера частиц объясняется сопутствующим повышением относительной скоро¬сти движения газа и твердых частиц. Кроме того, при одинаковой влаж¬ности материала толщина пленки свободной влаги пропорциональна размеру частиц (количество влаги пропорционалцно кубу размера; сво¬бодная плата распределяется по поверхности, пропорциональной квад¬рату размера). Понятно, что газовый поток легче срывает влагу с плен¬ки большей толщины, т. е. с более крупной частицы. Эта же причина вызывает увеличение N1 с ростом влажности материала.
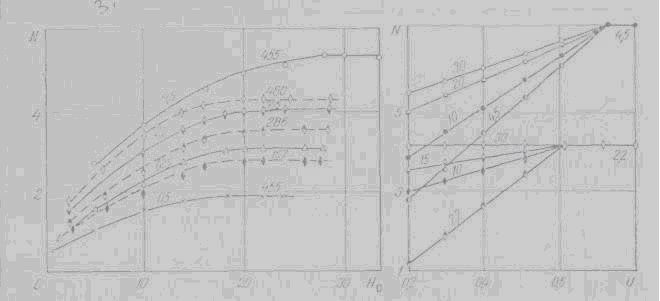
Рис. 3 - Влияние высоты слоя Hо, мм на интенсивность срыва N при влажности материа¬ла U= 0.2 кг влаги/кг сухого вещества. Сплошные линии — скорость газа Wс=455 м/сек; цифры у кривых слева — размеры частиц d, мм; штриховые линии — размер частиц 2,2 мм. Цифры у кривых справа — скорость, газа, Wс, м/с.
Рис. 4 - Зависимость числа срыва от влажности материала U, кг влаги/кг сухого материа¬ла при скорости газа Wс = 455 м/сек и различных высотах слоя. Цифры у кривых справа — размеры частиц, мм; цифры у кривых — значения Ho, мм.
Постоянство Nгр при U>=Uгр, видимо, объясняется ограниченной не¬сущей способностью среды в двухфазных потоках [4]. Одновременно на вынос влаги, сорванной с поверхности твердых частиц, может оказывать влияние их отбойное действие. В этом аспекте вполне объяснимо полу¬чение меньших значений Nгр и Uгр в случае частиц малых размеров, об¬ладающих большей суммарной поверхностью (рис. 1).
Возрастание величин N1’, N и Nгр с ростом Wс объясняется повышени¬ем относительной скорости газа и частиц, а также транспортирующей способности потока по жидкой фазе. Именно возрастанием последней при повышении Wс вызвано, вероятно, увеличение граничной влажно¬сти Uгр
Рост N с увеличением высоты слоя при умеренных значениях Ho об¬условлен увеличением абсолютного количества влаги в слое, а также продолжительности контакта твердых частиц с газовым потоком. По¬стоянство N при высоких Ho является следствием отбойного действия частиц. При этом предельное значение Hкр закономерно (см. выше) рас¬тет с увеличением размера частиц.
В основу обработки экспериментальных данных был положен анализ влияния параметров процесса па срыв влаги при толщине слоя в одну частицу.
Из рис. 1 видно, что прямые N1 = N1(U) для разных скоростей Wс в пределах каждого размера частиц (2,2 и 4,5 мм) пересекаются в однойточке с абсциссой Uкр (пупктнрн;ые прямые вблизн Uкр). Ордината точ¬ки пересечения N1’ зависит от размера частиц (для частиц диаметром 1,25 и 0,5 мм значения N1’ находили как ординаты линий N1 = N1(U) при абсциссе Uкр. Статистическая обработка опытных данных привела к следующей зависимости:
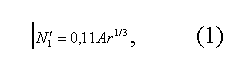
Для описания изменения N1 с U необходимо зафиксировать также ко¬нечную точку прямой с координатами Nгр, Uгр. Полученные нами эмпирические формулы отражают влияние размера частиц и скорости газа (рис 1 и 2)
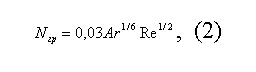

Формулы (1)—(3) получены в диапазоне
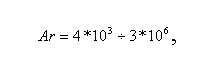
Располагая крайними точками прямых N1= N1 (U), легко построить обоб¬щенную зависимость для всего литейного участка, пользуясь приведенными числами срыва N
* и влажности U
*
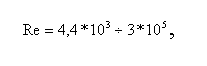
По уравнению (4) можно определить число срыва N, при заданной влажности U в диапазоне от 2Uкр до Uгр.
Переходя к расчету числа срыва для слоя произвольной высоты Ho, подчеркнем, что граничная точка (т. С. Численные значения Nгр и Uгр) не зависит от Ho (см. рис. 4). Анализ данных (рис. 3) показал целесооб¬разность их представления и относительных координатах N/N1 и Ho/d. При такой обработке экспериментальные точки для разных скоростей газа, размеров частиц и высот слоя располагаются с приемлемым раз¬бросом около общей кривой, описываемой простым соотношением
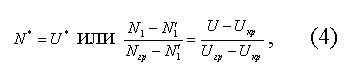
Зависимость (5) получена в диапазоне Ho/d = 1/36. Этой зависимости, разумеется, не подчиняются экспериментальные данные за пределами критической высоты слоя Hкр: в случае Ho > Hкр интенсивность срыва остается неизменной и максимально возможной для частиц данного размера при дан¬ной.скорости газа. Для нахождения высоты Hкр, при превышении которой N =N1=Nгр = const, предлагается эмпирическая формула
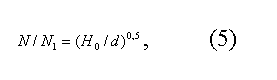
Литература
- Кваша В.Б., Чижов В.В., Хим. И нефт. Машиностроение,№ 6,1974.
- Гельперин Н.И.,Анштейн В.Г., Кваша В.Б, Основы техники псевдоожижения . М., «Химия» 1967.
- Псевдоожижение (под редакцией И. Дэвидсона и Д.Харрисона), гл Х. Пер. с англ под ред. Н.И. Гельперина. М., «Химия», 1974.
- Забродский С.С. Гидродинамика и теплообмен в псевдоожиженном слое. М.-Л., Госэнергоиздат, 1963.
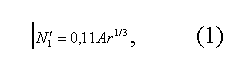 Для описания изменения N1 с U необходимо зафиксировать также ко¬нечную точку прямой с координатами Nгр, Uгр. Полученные нами эмпирические формулы отражают влияние размера частиц и скорости газа (рис 1 и 2)
Для описания изменения N1 с U необходимо зафиксировать также ко¬нечную точку прямой с координатами Nгр, Uгр. Полученные нами эмпирические формулы отражают влияние размера частиц и скорости газа (рис 1 и 2)