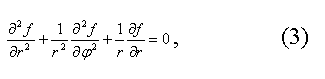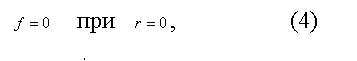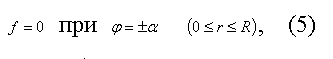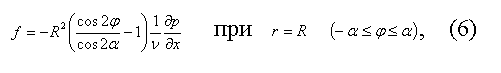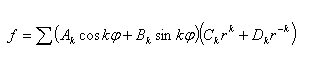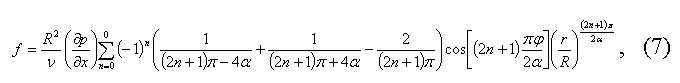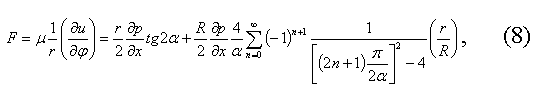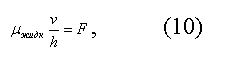Левич В.Г.

Физико-химическая гидродинамика. - Москва: Изд-во физ.-мат. литер., 1959. - 700 с.

         Метод «сдувания» тонких пленок жидкости.          Одним из важных случаев течения весьма тонкой пленки жидкости является течение ее под воздействием воздушного потока, движущегося над ее поверхностью. Течение таких пленок было использовано в предложенном Б. Л. Дерягиным и разработанном в многочисленных работах Б. В. Дерягина, М. М. Кусакова и их сотрудников методе определения гидродинамических характеристик жидкости.

         Как будет видно из излагаемой ниже теории метода, кото¬рый был назван «методом сдувания», он позволяет получить полную характеристику гидродинамических свойств жидкостей, обладающих как нормальной, так и аномальной (неньютоновской) вязкостью при проведении одного опыта. Рассмотрим движение жидкой пленки, увлекаемой воздухом, который продувается через клиновидную щель, образованную двумя плоскостями, расположенными под углом 2а (рис. 1) и имеющими радиус R. Жидкость нанесена на горизонтальную плоскость.

         Предположим, что движение воздуха происходит с такими скоростями, что соответствующее число Рейнольдса достаточно мало для сохранения строго ламинарного режима течения.          Поскольку толщина слоя жидкости на стенке весьма мала, ею при рассмотрении движения воздуха можно пренебречь. 'Тогда воздух представляет вязкую жидкость, протекающую через капилляр, имеющим вид сектора с радиусом R и углом раствора 2a. Если известно распределение скоростей воздуха, протекающего через щель, легко найти вязкое напряжение, действующее на поверхность жидкой пленки. Это напряжение будет, очевидно, различным на разных расстояниях от вершины щели. Поэтому на разных участках пленки течение ее будет происходить под действием разных напряжений. Это, как будет показано ниже, позволяет получить полную характеристику гидродинамических свойств пленки.

Рис. 1 - Клиновидная щель. Движение воздуха в щели происходит в одном измерении, вдоль оси х, со скоростью u. Уравнение Навье – Стокса в цилиндрических координатах имеет вид

         При этом градиент давления является постоянным по всей щели:

         Для упрощения вида граничных условии удобно ввести новую неизвестную функцию

         Функция удовлетворяет уравнению

         и граничным условиям:

        

        

         отвечающим обращению в нуль скорости воздуха на периметре щели. Функция f, удовлетворяющая уравнению (3) и граничным условиям (4) — (6), может быть найдена из общего решения уравнения (3)

         При соответствующем подборе k и постоянных Аk, Вk, Сk и Dk. Эта функция имеет вид

         Подставляя значение f в выражение (2), можно найти распределение скоростей воздуха в клиновидной щели. Напряжения трения, действующие на пленку жидкости, имеют вид

         Напряжение трения обращается в нуль при r=0 и при R= r. При малых углах раствора сумма ряда мала по сравнению с первым членом, так что

         Под действием напряжения F пленка, имеющая толщину h, приходит в движение со скоростью v, определяемой соотношением

         В опыте толщина h и скорость v измеряются интерферометрически. Первая - непосредственно, а вторая по скорости перемещения интерференционных полос в процессе сдувания.

         Таким образом, при помощи уравнения (10) в одном измерении можно определить вязкость жидкости как функцию действующего на нее напряжения трения. Для нормальных жидкостей

         Эта функция имеет вид прямой, проходящей через начало координат. Вместе с тем, метод сдувания позволяет найти толщину слоя жидкости, обладающего подвижностью. Иными словами, интерферометрические измерения позволяют определить то расстояние до поверхности твердой стенки, на котором частицы жидкости могут перемещаться относительно стенки.

         Измерения показали, что это расстояние не превышает 1/5*10000000 см. Это значение следует считать наиболее точным для минимальных расстояний до твердой поверхности, на которых жидкость сохраняет подвижность.

        Метод сдувания и различные его модификации нашли широкое применение в исследовании различных гидродинамических свойств жидкости.