В библиотеку
Векторное управление статорной обмотки индукционной машины при магнитном насыщении
Heath Hofmann, Студент, член, IEEE, Seth R. Sanders, член, IEEE, и Чарльз Р. Сулливан, член, IEEE
Материал взят здесь из электроного журнала IEEE TRANSACTION ON INDUSTRY APPLICATIONS, VOL.33,NO 4, JULY/AUGUST 1997. стр.935-944.
В данном разделе приведены переведенные главы из работы Stator-Flux-Based Vector Control of Induction Machines in Magnetic Saturation. Авторы указаны выше. Англоязычная версия не приведена из-за ее большого объема. В полном обьеме на языке оригинала статью можно прочесть в журнале ассоциации IEEE, все нужные для поиска реквизиты указаны выше.
1.Введение
Индукционные машины обычно моделируются исходя из постоянства магнитного поля. Однако во многих моделирующих прикладных программах, можно работать с перемененным потоком. Такое отношение к магнитному насыщению позволяет повысить их производительность. Например в моделирующих прикладных программах размеры индукционной машины могут быть установлены для нормальных рабочих условий. Но все же может возникнуть необходимость, произвести быстрое насыщение, чтобы преодолеть экстремальные значения, возникающие при большом ускорении или замедлении. Может использоваться меньшая машина, если ее система управления работает должным образом в течении периода магнитной насыщаемости. В системе ориентированной на управление потоком ротора, основанной на линейных магнитных параметрах, магнитная насыщенность в машине может вызывать эффекты перекрестного сцепления, которые снижают эффективность [1]-[8], а также приводят к ошибкам пир оценке потока ротора.
Наша более ранняя работа [9] и ряд других работ [5], [10] - [12], показали, что адекватность может быть достигнута, управлением потока ротора при знании закона управлении потоком магнитной насыщаемости. К сожалению этот подход требует чтобы, данные были сняты с реальных машин – для определения характеристик магнитной насыщенности. Следовательно желательно применение более простой и здравой схемы управления.
Статорный поток ориентируемый на свое управление, был разработан ка возможная альтернатива [13] - [24]. Оценка статорного потока на требует знания магнитных параметров, и следовательно потребности их снятия при магнитной насыщенности. Кроме того, схемы управления регулирования потока не должны зависеть от магнитных параметров. Значит этот метод – ориентируемый на управление – потенциально более здравый и его проще осуществлять в области насыщенности роторной обмотки управления. В этой статье будет показана методика работоспособности статорного потока, даже тогда когда индукционная машина работает в магнитной насыщенности. Мы представляем анализ проекта управления независимого от магнитных параметров. Мы также определили эту область управления, схему использующую нелинейную магнитную модель для машины, включающую насыщенность обмоток. Эксперименты проводились на 3-х фазной, 4-х полюсной машине. Показана процедура управления на уровне момента вращения.
Рисунок 1. Статор-ротор в два паза.
2. Магнитная схема моделирования.
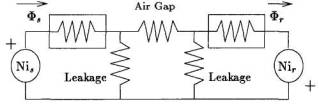
Наши моделируемые уравнения основаны на линейной модели магнитных параметров индукционной машины, разработанные в [25]. Модель получена по магнитной схеме статор - ротор (см. Рис. 1 и 2). Мы принимаем ту насыщенность, которая есть в опорах зубов ротора и статора. Из этой магнитной схемы мы получаем электирческую схему для статор - пара зуба ротора (см. рис. 3).
Рисунок 2.Магнитная схема статор-ротор в два паза. Составные элементы не линейны.
Рисунок 2.Электрическая схема статор-ротор в два паза. Составные элементы не линейны.
Катушки индуктивности нелинейные по отношению к текущему потоку . Они функционально объясняют насыщенность в статоре и зубцах ротора и приняты, чтобы быть монотонизирующими и проходить по основанию. Эффекты гистерезиса будут игнорироваться, потому что потребовало бы ввода дополнительных переменных. Эти недостатки устраняются линейной моделью пары зуба.
. Они функционально объясняют насыщенность в статоре и зубцах ротора и приняты, чтобы быть монотонизирующими и проходить по основанию. Эффекты гистерезиса будут игнорироваться, потому что потребовало бы ввода дополнительных переменных. Эти недостатки устраняются линейной моделью пары зуба.
Прогрессируя от модели отдельной пары зуба к модели в которой индукция в машине симметрична, мы принимаем воздушный зазор постоянным. Подводя итог можно сказать, что модель индукционной машины получена усреднением потока всех зубцов, принимая в расчет охлаждение статора и ротора для определения эффективного числа поворотов на зуб. Мы принимаем две стадии проветривания (прямая и квадратурная), отметим что эти стадии можно комбинировать для моделирования третьей стадии – вьющейся. Итог – эквивалент электрической схемы статора – пары зуба ротора. рис.3 Переменные для прямого и квадратичного проветривания представлены в векторной форме например
| |
 |
(1) |
Нелинейные катушки индуктивности индукционной машины описаны векторными функциями вида 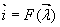 . Вектор направления , также как и направления , и симметрия вращения зависит только от .В итоге исходя из этих ограничений
. Вектор направления , также как и направления , и симметрия вращения зависит только от .В итоге исходя из этих ограничений  можно записать так
можно записать так
| |
 |
(2) |
Где функция  – скалярная функция имеющая форму подобную характеристике насыщенности отдельно взятого зуба, но показано как комбинация насыщенности стали во многих зубах задействованных. Отношение текущего потока машины можна тогда представить следующим образом
– скалярная функция имеющая форму подобную характеристике насыщенности отдельно взятого зуба, но показано как комбинация насыщенности стали во многих зубах задействованных. Отношение текущего потока машины можна тогда представить следующим образом
| |
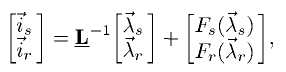 |
(3) |
где
| |
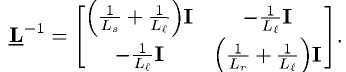 |
(4) |
Измерения выполнены на 3-х фазной машине, при 1800 об/мин. Индукционная машина адекватна вышеупомянутой модели [25].
В [25] показано, что при мгновенном вращающем моменте, в машине с тремя стадиями (включая эффекты насыщения) использование нелинейной модели может быть записано как
модели может быть записано как 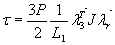 ,
Где
,
Где  номер пар полюсов машины,
номер пар полюсов машины,  верхний индекс обозначает перемещение вектора и
верхний индекс обозначает перемещение вектора и ортогональной матрицы вращения
ортогональной матрицы вращения
Используя то что  можем получить другое выражение для момента вращения
можем получить другое выражение для момента вращения
| |
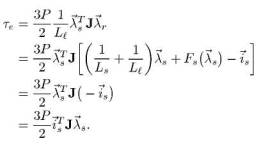 |
(5) |
Точность вышеизложенного выражения для вращающего момента была подтверждена на эксперементом в [26] мы обращаем внимание на это для индукционной машины с беличьей клеткой имеющий насыщаемый материал – при изменении пар полюсов насыщенность в зубцах ротора может приводить к потерям в роторе. Как показано в приложениях, вышеуказанные выражения для вращающего момента справедливы при условии утечек в насыщенном режиме.
3. Управление вращающим моментом.
Мы выбирает поток статора и векторы потока ротора в нашей системе обособленными, у статора текущий вектор как итог в обособленных уравнениях в произвольной форме рекомендуется (верхний индекс х) тогда приведены (см.[9].[25])
| |
 |
(6) |
где
| |
 |
(6) |
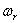 – угловая скорость ротора.
– угловая скорость ротора.
Переменная 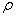 показывает угол на котором основаны обособленные уравнения. Рекомендуется постоянная форма (верхний индекс
показывает угол на котором основаны обособленные уравнения. Рекомендуется постоянная форма (верхний индекс 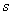 ) соответственно , и рекомендуемая электрическая форма записи относительно потока статора (верхний индекс
) соответственно , и рекомендуемая электрическая форма записи относительно потока статора (верхний индекс  ) соответствует
) соответствует 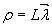 . В этом случае
. В этом случае  – электрическая частота.
Выбирая угол потока статора для нашей рекомендуется устанавливать
– электрическая частота.
Выбирая угол потока статора для нашей рекомендуется устанавливать  , и
, и 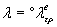 . Значит рекомендуемая схема потока статора (29), написана как
. Значит рекомендуемая схема потока статора (29), написана как
| |
 |
(7) |
Ограничения в (6) есть итогом для выражения электрической частоты
| |
 |
(8) |
Используя эту информацию, мы перезаписываем обособленные уравнения санаторного потока ссылаясь на схему рассматривающую только статорный поток и текущую динамику квадратичности статора.
Эти уравнения предполагают, что вращающий момент может управляться используя  , чтобы управлять
, чтобы управлять  и
и 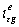 управлять . Для компенсации падения напряжения имеющего сопротивление
управлять . Для компенсации падения напряжения имеющего сопротивление можно применить пропорционально –интегральный регулятор управления
можно применить пропорционально –интегральный регулятор управления
| |
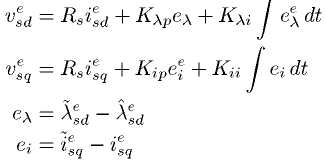 |
(9,10) |
Где  и
и  фиксированные значения, и оцениваемый или измеренный поток статора, хотя другие схемы управления тоже могут использоваться, мы начинаем с PI регулятора из-за его простоты.
фиксированные значения, и оцениваемый или измеренный поток статора, хотя другие схемы управления тоже могут использоваться, мы начинаем с PI регулятора из-за его простоты.
По этой схеме управления динамика потока статора дается
| |
 |
(11) |
Значит поток статора может регулироваться если его оценочный или измеренный поток статора согласованы с его фактическими значениями. Кроме того на устойчивость динамики потока влияет динамика системы.
В прикладных программах может изменяться с температурой, и поэтому трудно упредить падение напряжения при имеющемся сопротивлении. Однако эта погрешность вносит небольшое возмущение, но серьезно не затрагивает управление при достаточно планируемом увеличении.
Поскольку динамика в рекомендуемой схеме потока статора не линейная (даже если приняты линейные магнитные параметры) мы начинаем линеаризацию их относительно установившихся действующих точек, чтобы
| |
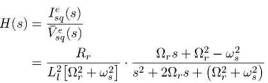 |
(12) |
Мы характеризуем установившуюся операционную точку частотой и величиной потока статора. При этом динамика потока статора с беличьей клеткой отличалась от остальных в системе, но мы полагаем величину потока статора постоянной – поскольку мы провели линеаризацию. функция преобразования в линеаризованной системе выглядит так 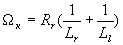 мы вычисляем эту частоту, чтобы было 160 рад/с для 3-х фазной индукционной машины.
мы вычисляем эту частоту, чтобы было 160 рад/с для 3-х фазной индукционной машины.

 . Они функционально объясняют насыщенность в статоре и зубцах ротора и приняты, чтобы быть монотонизирующими и проходить по основанию. Эффекты гистерезиса будут игнорироваться, потому что потребовало бы ввода дополнительных переменных. Эти недостатки устраняются линейной моделью пары зуба.
. Они функционально объясняют насыщенность в статоре и зубцах ротора и приняты, чтобы быть монотонизирующими и проходить по основанию. Эффекты гистерезиса будут игнорироваться, потому что потребовало бы ввода дополнительных переменных. Эти недостатки устраняются линейной моделью пары зуба.

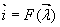 . Вектор направления , также как и направления , и симметрия вращения зависит только от .В итоге исходя из этих ограничений
. Вектор направления , также как и направления , и симметрия вращения зависит только от .В итоге исходя из этих ограничений  можно записать так
можно записать так

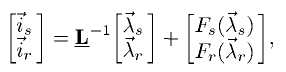
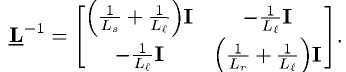
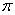 модели может быть записано как
модели может быть записано как 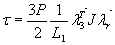 ,
Где
,
Где  номер пар полюсов машины,
номер пар полюсов машины,  верхний индекс обозначает перемещение вектора и
верхний индекс обозначает перемещение вектора и ортогональной матрицы вращения
ортогональной матрицы вращения
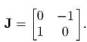
 можем получить другое выражение для момента вращения
можем получить другое выражение для момента вращения
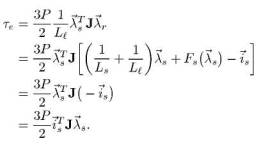


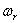 – угловая скорость ротора.
– угловая скорость ротора.
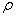 показывает угол на котором основаны обособленные уравнения. Рекомендуется постоянная форма (верхний индекс
показывает угол на котором основаны обособленные уравнения. Рекомендуется постоянная форма (верхний индекс 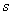 ) соответственно , и рекомендуемая электрическая форма записи относительно потока статора (верхний индекс
) соответственно , и рекомендуемая электрическая форма записи относительно потока статора (верхний индекс  ) соответствует
) соответствует 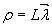 . В этом случае
. В этом случае  – электрическая частота.
Выбирая угол потока статора для нашей рекомендуется устанавливать
– электрическая частота.
Выбирая угол потока статора для нашей рекомендуется устанавливать  , и
, и 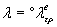 . Значит рекомендуемая схема потока статора (29), написана как
. Значит рекомендуемая схема потока статора (29), написана как


 , чтобы управлять
, чтобы управлять  и
и 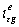 управлять . Для компенсации падения напряжения имеющего сопротивление
управлять . Для компенсации падения напряжения имеющего сопротивление можно применить пропорционально –интегральный регулятор управления
можно применить пропорционально –интегральный регулятор управления
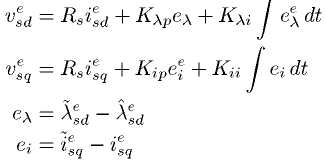
 фиксированные значения, и оцениваемый или измеренный поток статора, хотя другие схемы управления тоже могут использоваться, мы начинаем с PI регулятора из-за его простоты.
фиксированные значения, и оцениваемый или измеренный поток статора, хотя другие схемы управления тоже могут использоваться, мы начинаем с PI регулятора из-за его простоты.

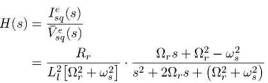
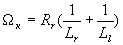 мы вычисляем эту частоту, чтобы было 160 рад/с для 3-х фазной индукционной машины.
мы вычисляем эту частоту, чтобы было 160 рад/с для 3-х фазной индукционной машины.