|
|
|
Наука розширює межі пізнання згідно з принципом: “A potentia ad actum” – “Від можливого до дійсного”. У зв'язку з цим перед сучасним дослідником постають усе більш складні задачі, отримання розв'язків для яких методами класичного математичного аналізу неможливо.
Математична модель, яка формулюється, для практично будь-якої задачі характеризується системою взаємозв'язаних диференційних рівнянь з частковими похідними, аналітичний розв'язок якої неможливий. Це пояснюється складною геометрією об'єктів, що досліджуються; одночасним проходженням та взаємним впливом наступних процесів: гідродинамічних ламінарних та турбулентних течій, різноманітних видів тепломасообміну, електричних та магнітних явищ; неєдиним розв'язком диференційних рівнянь з частковими похідними тощо.
Усі зазначені процеси в різноманітних комбінаціях відбуваються у теплових агрегатах (промислових печах, котельних установках, ТВЕЛах ядерних реакторів, МГД генераторах тощо).
Таким чином, практично єдиним засобом для знаходження розв'язку важливих практичних задач є чисельні методи. Піонерами в області обчислювальних технологій є обчислювальна гідродинаміка та теплообмін, які є базовими для реалізації математичного моделювання процесів переносу в технічних агрегатах та явищах природи.
Мета магістерської дисертації – отримати розв'язок системи диференційних рівнянь, які описують конвективний теплообмін та дифузійні процеси у теплоенергетичному агрегаті (парогенераторі) у двовимірній декартовій системі координат за допомогою проведення чисельного експерименту. Також в роботі планується визначити локальну зміну коефіцієнта тепловіддачі α на усіх поверхнях теплового агрегату.
Математична модель задачі складається з наступної системи рівнянь.
Рівняння руху рідини у проекції на вісь X:

Рівняння руху рідини у проекції на вісь Y (з урахуванням масової сили або сили тяжіння):
 ,
,
де
![]() – компоненти тензора в'язких напружень:
– компоненти тензора в'язких напружень:


Рівняння суцільності:
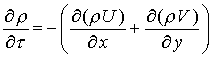
Рівняння теплопровідності у рухомих середовищах (рівняння Фур'є – Кірхгофа):
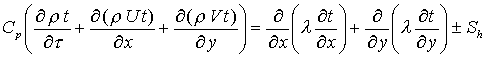
Рівняння теплопровідності (рівняння Фур'є) для твердих тіл:

Рівняння зв'язку:

При дослідженні процесів горіння ця система доповнюється ще трьома рівняннями месопереносу. Якщо припустити, що між пальним та окислювачем проходить необоротна одностадійна екзотермічна хімічна реакція:
![]() ,
,
де Г – пальне; О – окислювач; ПГ – продукти горіння; νi – стехіометричні коефіцієнти, то для області, що досліджується рівняння дифузії для пального та окислювача будуть мати вигляд:

 ,
,
де Cг = ρг / ρ – відносна масова концентрація пального; Cок = ρок / ρ – відносна масова концентрація окислювача; mг и mок – швидкості витрачання пального та окислювача лише в єдиній хімічній реакції. Для продуктів горіння можна записати – Cпг = ρпг / ρ.
Таким чином, сума усіх відносних масових концентрацій дорівнює одиниці. Отже, відносна масова концентрація продуктів горіння визначається з рівняння:
![]()
Наведена система рівнянь доповнюється умовами однозначності, які містять:
Геометричні умови, які визначають форму та розміри області, у якій проходить процес, що досліджується;
Фізичні умови, які задаються теплофізичними властивостями речовини, яка заповнює область, що досліджується. Також ці умови враховують розподіл внутрішніх джерел та стоків теплоти по об'єму;
Часові (початкові) умови містять розподіл вихідної величини в області, що досліджується у початковий момент часу;
Граничні умови, які визначають особливості проходження процесу на границях області, що досліджується.
Розв'язок перших трьох рівнянь (розрахунок поля течії) передбачається отримати за допомогою методу SIMPLER. Знаходження розв'язків рівнянь теплопровідності у рухомих середовищах та твердих тілах, а також рівнянь дифузії для пального та окислювача здійснюється за умови відомих полей складових швидкості U, V за допомогою програми CONDUCT.
Розв'язуючи поставлену задачу за допомогою чисельних методів отримаємо розподіл складових швидкості U та V, тиску, температури, концентрацій: Cг, Cок, Cпг у всій області теплового агрегату, що досліджується.
| На головну сторінку |
© Created by Y. Boev, 2006