URL: http://cs.donntu.ru/~zinchenk/art/SintezASA.rar

Первоисточник: Сборник трудов Донецкого государственного технического университета. Серия: Информатика, кибернетика и вычислительная техника, выпуск 6. - Донецк: ДонГТУ, 1999.- С. 186-191.

Назад в библиотеку.

СИНТЕЗ ОПТИМАЛЬНЫХ СТРУКТУР АСИНХРОННЫХ СИГНАТУРНЫХ  АНАЛИЗАТОРОВ

 

Зинченко Ю.Е.

Кафедра ЭВМ ДонНТУ

zinchenko@cs.donntu.ru

 

Abstract

Zinchenko.J.J Syntesis of the optimum asynchronous signature analizators. The theory of the asynch-ronous compact analysis of digital circuits is considered. The   asynchronous analizers based on a binary counter and  a  signature register(ASR) and  their probability characteristics are de-scribed. Based on the theoryof asynchronous compact analysis the optimum ASR are designed.

 

Введение

К настоящему времени в области компактного анализа тестовых реакций (ТР) цифровых устройств (ЦУ) наибольшее применение нашли счетные схемы (СС) и сигнатурные анализаторы (СА) [1-11]. 

Сжатие тестовых реакций (ТР) в этих анализаторах производится по синхроим-пульсам, т.е. анализаторы являются синхронными устройствами.  Однако, в ряде случаев, когда имеет место асинхронный об­мен информацией, например, в системах типа "запрос-ответ", к ко­торым можно отнести сетевые устройства, более предпочтительным, а иногда и единственно возможным оказывается асинхронный компактный анализ  (АКА).

Асинхронные анализаторы имеют некоторые преимущества и при сжатии синхронных ТР. Так при асинхронном анализе упрощается расчет эталон­ных сигнатур, так как отпадает необходимость в знании тонкостей синхронизации объекта диагностики (ОД), что позволяет использовать для расчета более крупные, чем структурные, модели ОД, например, функциональные, алгоритмические и т.д.. Кроме того, в общем случае состояние асинхронного анализатора  изменяется  гораздо  реже синхронного,  благодаря чему уменьшается объем ди­агностической информации, снижаются затраты на ее хранение и упрощается локализация первой ошибки ТР.

Срабатывание элементов памяти асинхронного анализатора производится по  функции самой анализируемой последовательности, точнее по изменению значений ее элементов.   Среди подобного рода анализаторов исторически  первой стала применятся тривиальная схема на базе асин­хронного счетчика, которая производит подсчет перепадов (фронтов) одноразрядной ТР [1,8,9,11]. Имея хоро­шие вероятностные характеристики (ВХ) по "средней" ошибке [1], такой анализатор плохо обнаруживает "кратные" ошибки [11] и неэффекти­вен при сжатии параллельных потоков ТР.

Поиску и исследованию новых структур асинхронных КАТР посвя­щена работа [12], где  формализуется метод АКА, рас­крываются механизмы сжатия и компенсации ошибок,    вводятся  два класса асинхронных КАТР - асинхронные счетные схемы (АСС) и асин­хронные сигнатурные анализаторы (АСА).  Здесь же выводятся формулы в общем виде для  определения ВХ этих КАТР, на основе которых проводится их сравнительная характеристи­ка.  С одной стороны такой анализ показал, что АСС в целом неэф­фективна для компактного анализа,  а с другой - АСА, соче­тая  в себе высокую обнаруживающую способность регистра  сдвига  с линейными обратными связями (РСЛОС),  на базе которого он строит­ся, с асинхронным принципом срабатывания может эф­фективно использоваться для компактного анализа параллельных  по­токов ТР.  Поиску эффективных структур АСА и посвящается  настоя­щая  работа.

1.  Асинхронный компактный анализ тестовых реакций ЦУ

Тестовое диагностирование ЦУ по клас­сической схеме подразумевает использование генератора и анализа­тора тестов, подключаемых к внешним выводам ЦУ. В случае компактного  тестирования накладываются жесткие ограничения по аппаратур­ным затратам, поэтому генератор и анализатор должны быть компак­тными. ТР W, формируемая под воздействием тестовой последовательности (ТП) Т,  которая поступает с  генератора тестов ГТ, сжимается компрессором КТР (устройство сжатия последо­вательности)  в сигнатуру N для дальнейшего сравнения её с эталон­ной сигнатурой N^э.  Компрессор и последовательно соединенный с ним компаратор образуют КАТР :

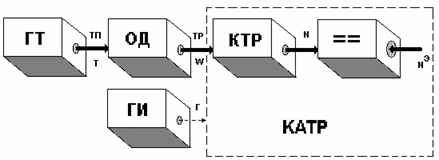
Компрессор обычно является последовательностным устрой­ством и может син-хронизироваться синхросерией Г либо использо­вать для этого саму сжимаемую последо-вательность W. В первом слу­чае анализатор и реализуемый им метод сжатия будем назы-вать синхронным , во втором случае - асинхронным. При этом ТР будем также называть синхронной (асинхронной), если она вырабатывается синхронным (асинхронным) ОД.

Среди синхронных КАТР наибольшее распространение получили СА и СС [1-6,10]. Основу СА составляет РСЛОС , СС вы­полняются на базе двоич­ного счетчика (СТ).  Сравнительный анализ СС и СА позволяет сделать выбор в пользу последнего, в особенности при сжатии параллельных потоков ТР [10].

Компрессор ТР ассинхронного КАТР кроме собственно компрессора (СТ либо РСЛОС ) включает в свой состав узел синхронизации (УС), задачей которого является формирование короткого синхроимпулься по заданной функции от элементов ТР. Такие анализаторы в [12] предлагается представлять дву­мя классами - АСС и АСА:

            

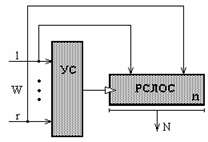
               а                                                                   б

                                Рис.2.  АСС (а) и  АСА (б) в общем виде

 

 Принципиальным отличием АСА от АСС является то, что первый не только фиксирует факт возникновения импульса, вырабатываемого узлом УС, но и сжимает входной вектор, выз­вавший возникновение импульса. Узел УС состоит из комбинационной схемы (КС) с выходной функцией f,  одновибраторов (ОВ) и имеет две модификации,  представленные на рис.3, которые мы будем обозначать как УС1 и УС2.

Проявление неисправностей в ТР ОД носит вероятностный характер и обычно описывается "равномерным" и "кратным" механизмами. Равномерный механизм, на основе которого решается поставленная задача в данной работе, описывается следующими вероятностными характеристиками  [1,3,4,6,11,12 ] :

- Р(t) -  "частная" вероятность – вероятность необнаружения средней ошибки в              предположении, что компактному анализу подвергаются    равновероятные ТР,  сигнатура которых равна t ;

- Р= -  "средняя" вероятность – вероятность необнаружения   средней ошибки в предположении, что равновероятна любая ТР .

             Рис.3. Узел синхроникации типа 1 (а) и типа 2 (б)

2. Асинхронные сигнатурные анализаторы

Асинхронный компактный анализатор, в качестве компрессора данных кото­рого выступает РСЛОС, называется асинхронным сигнатурным анализатором [12]. В зависимости от модификации УС будем различать два типа анализаторов – АСА типа 1 (АСА1) и АСА типа 2 (АСА2). Cтруктуры таких анализаторов приведены  на рис 4.

 

      

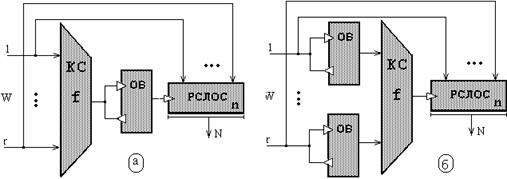
                     Рис.4.  АСА типа 1 (а) и тпа 2 (б)  в общем виде

 

Под РСЛОС обычно подразумевают одну из двух эквивалентных  разновидностей  линейной последовательностной машины [3] :

       

                     а                                                                                    б            

             Рис.5. РСЛОС с внутренними (а) и внешними (б) сумматорами обратной связи

 

Для обеспечения наилучших характеристик РСЛОС коэффициенты   α_j, j=1,2,…,n,        подбира­ются таким образом, чтобы многочлен обратной связи был примитивным [1,3].

ВХ АСА по средей ошибке для ТР длиной m описываются вероятностями :

                   ( 1)

    

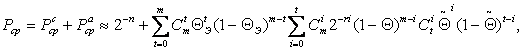
где  - синхронные составляющие вероятностей ;

      - асинхронные составляющие вероятностей ;

      -  параметр УС - вероятность появления синхроимпульса на выходе УС ;

       =  1 - 2 ;    =   / , C - число сочетаний по a из b .

3.  Синтез оптимальных анализаторов

 

Из (1) видно, что обнаруживающая способность АСА определяется  величинами: m, n, r и Θ. Первый из этих параметров не влияеет на структуру АСА, второй определяет разрядность РСЛОС , r и Θ определяют структуру и сложность УС.

При выборе n следует руководствоваться теми же соображениями, что и для син-хронного СА - РСЛОС розрядностью более 8 обеспечивает достаточно хорошие ВХ. Па-раметр r определяется розрядностью ТР. Остается определиться с выбором параметров Θ.

Поэтому задача построения опти­мального АСА (оптимального по некоторому классу) сводится, во-пер­вых, к выбору параметра   Θ_опт , при котором обеспечиваются мини­мальные вероятности P(t) и P_ср, и, во-вторых, - к построению узла УС_опт с параметром Θ_опт, который требует наименьших аппаратурных затрат среди всевозможных АСА (среди всевозможных АСА некоторого класса).

            Зафиксируем m, n и r и найдем Θ, при котором АСА будет обладать наилучшей обнаруживающей способностью по вероятностям  P(t) и   P_ср .

Пусть имеются асинхронные сигнатурные анализаторы АСА₁ с параметром Θ₁ и АСА₂ с параметром Θ₂. Обозначим  частную и среднюю вероятности некоторого АСА с па­раметром Θ как P^а(t,Θ) и P_ср^а(Θ). Тогда, если Θ₁>Θ₂ , то из  (1) следует,что P^а(t,Θ₁)< P^а(t,Θ₂) и P_ср(Θ₁) < P_ср(Θ₂), т.е. по ВХ АСА₁ предпочтительнее АСА₂.

Отсюда следуют следующие утверждения: а) наилучшей обнаруживающей способностью по "средней" ошибке обладает АСА,  параметр Θ которого равен верхней возможной границе: Θ_опт = Θ_мах = Θ^э = 1-2^-r ;  б) среди всевозможных АСА одинаковой разрядности предпочтительнее анализатор, у которого параметр Θ  больше по величине.

Найдем параметры Θ_опт1, Θ_опт2 оптимальных АСА по описанным выше классам АСА типа 1 и типа 2. Пусть АСА₁ принадлежит типу 1 а АСА₂ - типу 2, причем их узлы УС₁ и УС₂ построены на базе ком­бинационных схем КС₁ и КС₂ соответственно.

Одновибратор ОВ, входящий в состав УС,  можно представить моделью , построренной на элементе задержки и сумматоре «по модулю два» :

 

 

Пусть вероятность появле­ния "1" на входе  x равна  p(x), а на входе y - p(y),  причем входные величины на входе  x   взаимонезависимы. Так как на его выходе реализуется функция вида y= xd,  то вероят­ность появления "1" на выходе  y равна :

                                          p(y) = p(x)( 1-p(d ) ) + p(d) ( 1- p(x) )  .

          Предполагая равновероятным появление "1"  для  всех  входных сигналов (p(x)=g) при нулевом  начальном  состоянии  элемента задержки получаем искомую вероятность  p(y)=g в начальный момент времени и p(y)=2g в последующие моменты времени, а также  ее  математическое ожидание M[y]:

          M[y] = (g+2g(1-g)(m-1))/m [y] = 2g(1-g),

 

что при g = 2   упрощается к виду: p(y) = M[y] = 2  .

Для определения параметра    УС₁ и  УС₂  составим  их эквивалентные схемы :

                                                                                                                  

                                Рис.7  Модель УС типа 1 (а) и типа 2 (б)

 

При расчете ВХ ТР W принято представлять поразрядной суммой "по модулю 2" эталонной ТР и последовательности ошибок:  W =WE ,  так что на  j-ом входе анализатора будут складываться их скалярные элементы :  w_i,j = w_i,j^э  е_i,j , то 

 

p(w) = p(w)+p(e) - 2p(w ) p(e) =  0.5 + 0.5 – 2 ∙ 0.5 ∙ 0.5 =  0.5 .

 

Отсюда следует, что вероятности сигналов на полюсах УС примут значения, показанные на рис.7. Тогда,  при  условии  равновероятности  "1" и "0"  на  входах  получаем для УС₁

 

 

                   

 

 

 

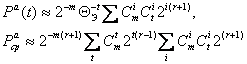
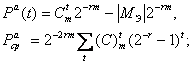
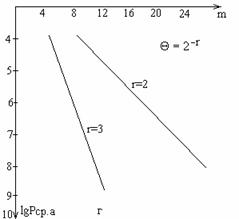
Рис. 8. Структура и графическая зависимость синхронной составляющей вероятности P_cp линейного (а, в) и линейный (б,г) оптимального АСА.

Θ₁ =2p(1-p), а для УС₂ – Θ₂ = p, где p - вероятность появления "1" на выходе КС.

Замечаем, что  Θ₁  p  1-2^-r, а Θ₂  Θ_опт2  1-2^-r и  Θ₁   Θ₂  Θ_опт .  Отсюда Θ_опт1=0.5, а Θ_опт2 = 1-2^-r. Схе­мы КС1 и КС2, реализующие параметры Θ_опт1   и Θ_опт2  с затратами, близкими к минимальным, можно построить на базе  r-входовых эле­ментов ИЛИ и ИСКЛЮЧАЮЩЕЕ ИЛИ  [13,14]. Структурные схемы и ВХ оптимальных АСА представлены на рис. 8. Из графиков видно, что с ростом m и r составля­ющие резко стремятся к нулю, так что уже при m > 30 ими можно принебречь. Поэтому для  оптимальных АСА можно принять P(t)  Pср  2^-n , что близко к характеристикам синхронного сигнатурного ана­лизатора.

 

Заключение

 

Проведенные исследования АСА позволяют сделать следующие выводы:

- оптимальный АСА по ВХ имеет па­раметр Θ_опт=1-2^-r , причем оптимальные АСА по типу 1 и типу 2 име­ют параметры Θ_{опт 1}= 2^-1  и Θ_опт2 = 1-2^-r соответственно;

- среди всевозможных АСА одинаковой разрядности предпочти­тельнее анализатор, у которого параметр Θ  больше по величине;

- при фиксированных n и с ростом r ВХ АСА улучшаются;

- для оптимальных анализаторов P(t) ≈ Pср ≈ 2^-n ;

- нелинейный АСА обладает наилучшими ВХ, линейный АСА - наиболее экономичен.

 

Литература.

 

1. Frohwerk R.A. Signature analisis: A new digital field service method. – Hewlett Packard J. 1977, N 5, p. 2-8.

2.  Swith I.F. Measures of the effectivenes of fault signature analisis. - IEEE Trans. Compuf. 1980. N 6, p. 510-514.

3. Кирьянов К.Г. К теории сигнатурного анализа - Техника средств связи. Сер. Радиоизмерительная техника. 1980, Вып. 2, с.1-46.

4. Ярмолик В.Н. Контроль и диагностика цифровых узлов ЭВМ. - Мн.: Наука и техника. 1988, - 240 с. 

5.  Тупкало В.П. Основы теории сигнатурного анализа цифровых систем: Монография. - Изд. МО Украины, 1994.- 324 c.

6.  Баран Е.Д. О достоверности контроля двоичных последователь­ностей методом счета состояний - Автоматика и вычислительная техника, 1982, N 6, с. 66-70.

7.  Hayes J.P. Transition count testing of combionational logic circuits - IEEE Trans. Comput., 1976, N 6, p. 613-620.

8.  Reddy S.M. A note on testing logic circuits by transition counting - IEEE Trans. Comput., 1977, N 3, p. 313-314.

9.  Fujiwara H., Kinoshita K. Testing logic circuits with compressed data - Digest of papers FTCS-8, 1978, p. 108-113.

10. Ярмолик В.Н., Канцельсон Е.И. Достоверность анализа методом счета единиц методом сигнатурного анализа - Автоматика и вы­числительная техника, 1986, N 3.

11.  Зинченко Ю.Е. Исследование обнаруживающей способности асинхронного счетчика // Электронное  моделирование, 1994, N2, c.58-61.

12. Зинченко Ю.Е. Компактное сжатие двоичных последовательнос­тей асинхрон-ным анализатором/ Ред. журн. "Электронное моделирова­ние". - Киев, 1988. -Деп. в ВИНИТИ 09.03.88. - 38с.

13. А.С. N1280634, МКИ G06F 11/00. Многоканальный сигнатурный анализатор / Зинченко Ю.Е;  Опубл. 30.12.87 Бюл. N48.

14. А.С. N1383359, МКИ G06F 11/00. Многоканальный сигнатурный анализатор / Зинченко Ю.Е.; Опубл. 23.08.88. Бюл. N11.

 

 Назад в библиотеку.

URL: http://cs.donntu.ru/~zinchenk/art/SintezASA.rar

Первоисточник: Сборник трудов Донецкого государственного технического университета. Серия: Информатика, кибернетика и вычислительная техника, выпуск 6. - Донецк: ДонГТУ, 1999.- С. 186-191.