Назад в библиотеку.

 

АНАЛИЗ ОБНАРУЖИВАЮЩЕЙ СПОСОБНОСТИ АСИНХРОННЫХ СИГНАТУРНЫХ  АНАЛИЗАТОРОВ НА КРАТНЫЕ ОШИБКИ

 

Зинченко Ю.Е.

Кафедра ЭВМ ДонНТУ

 zinchenko@cs.donntu.ru

 

Abstract

 

Zinchenko Y.Y. Analysis of multiple error detectivity of asynchronous signature analyzers. The asynchronous analyzers based on signature register and their probability characteristics are considered. Multiple error detection probability of asynchronous signature analyzers are parsed.

 

Введение

 

К настоящему времени в области компактного анализа тестовых реакций (ТР) цифровых устройств наибольшее применение находят синхронные счетные схемы и сигнатурные анализаторы [1-7]. Будучи эффективными по обнаруживающей способности такие анализаторы не могут применяться для сжатия асинхронных ТР.

 

Альтернативой синхронным компактным анализаторам ТР (КАТР) в этом аспекте являются асинхронные КАТР. Такие анализаторы имеют некоторые преимущества и при сжатии синхронных ТР: упрощается расчет эталонных сигнатур, уменьшается объем диагностической информации, снижаются затраты на ее хранение и упрощается локализация первой ошибки ТР [2,4,8-14].

 

Среди асинхронных КАТР исторически первым стал применяться асинхронный счетчик (АСТ). В [2] получены выражения для оценки вероятностных характеристик АСТ по "средней" и одиночной ошибке, в [10] эти результаты распространены на случай ошибок произвольной кратности. Анализ показал достаточно хорошие результаты по "средней" ошибке и неудовлетворительные по "кратным" ошибкам малой кратности. Кроме того, АСТ оказался неэффективным для сжатия параллельных ТР.

 

Более широкие и детальные исследования асинхронных КАТР выполняются в [11], где формализуется метод АКА, раскрываются механизмы сжатия и компенсации ошибок, вводятся два класса асинхронных КАТР - асинхронные счетные схемы (АСС) и асинхронные сигнатурные анализаторы (АСА).  Здесь же выводятся формулы в общем виде для  определения вероятностных характеристик этих КАТР, на основе которых проводится их сравнительная характеристика.

Анализ АСС показал, что наиболее эффективным представителем  АСС по вероятностным характеристикам является АСТ, однако такой анализатор не может эффективно использоваться для компактного анализа параллельных потоков ТР. С другой стороны АСА лишен описанного недостатка, сочетая  в себе высокую обнаруживающую способность регистра  сдвига  с линейными обратными связями (РСЛОС),  на базе которого он строится, с асинхронным принципом срабатывания. В наибольшей степени это относится к структурам АСА [13,14], эффективность которых по обнаруживающей способности на «средние ошибки» и по аппаратурным затратам была показана в [12].

 

Целью данной работы является исследование обнаруживающей способности  АСА по кратной ошибке.

 

1. Асинхронные сигнатурные анализаторы

 

АСА [11] строится на базе РСЛОС и узла синхронизации (УС):

 

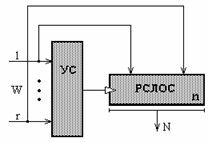
Рис.1  Асинхронный сигнатурный анализатор в общем виде

 

Под РСЛОС обычно подразумевают одну из двух эквивалентных  разновидностей  линейной последовательностной машины [3]. Для обеспечения наилучших характеристик РСЛОС коэффициенты усилителей обратной связи , подбираются таким образом, чтобы соответствующий многочлен обратной связи был примитивным [1,3].

 

       

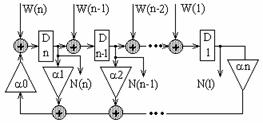
                     а                                                                                    б            

Рис.2 РСЛОС с внутренними (а) и внешними (б) сумматорами обратной связи

 

Задачей УС является выработка синхроимпульса РСЛОС по заданной функции, определяемой над элементами анализируемой ТР. Длительность синхроимпульса должна быть минимальной, но достаточной для срабатывания элементов задержки (D) РСЛОС. УС строится на базе комбинационной логической схемы (КС), реализующей функцию , и одновибраторов (ОВ), и имеет две модификации:

 

 

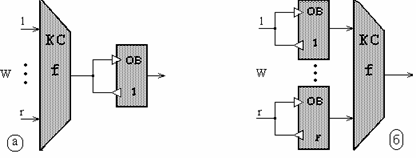
Рис.3 Узел синхронизации типа 1 (а) и типа 2 (б).

 

Конкретная модификация ACA получается в результате выбора типа УС и конкретизации его КС. Из всевозможных модификаций АСА в [12] синтезированы так называемые «линейный» и «нелинейный» оптимальные (по вероятности обнаружения «средней» ошибки и аппаратурным затратам) схемы АСА [13,14], которые представлены на рис.4. Выберем этих представителей АСА как наиболее эффективных в качестве объектов исследований данной работы.

 

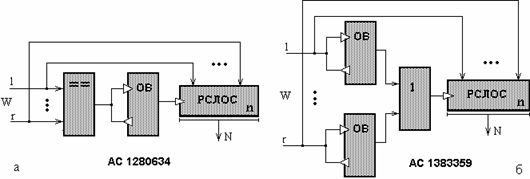
Рис.4 Оптимальный линейный (а) и нелинейный (б) АСА

 

Проявление неисправностей в ТР ОД носит вероятностный характер и обычно описывается "равномерным" и "кратным" механизмами. Кратный механизм, являющийся предметом исследований данной работы, описывается "кратной" вероятностью _, -  вероятностью необнаружения ошибки КАТР в предположении, что на эталонную ТР воздействуют только ошибки кратности , причем появление каждой из таких ошибок является событием равновероятным [1-4,10].

 

2.Исследование обнаруживающей способности

одновходового АСА на кратные ошибки

 

Рассмотрим одновходовой АСА, т.е. когда . Структура такого анализатора приведена на рис.5,а. По функциональным и вероятностным характеристикам такой анализатор эквивалентен ACT (рис. 5,б):

 

 

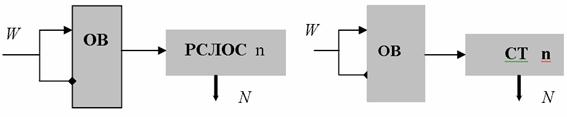
                          а                                                                           б

 

Рис.5. Одновходовой АСА (а) и эквивалетный ему асинхронный счетчик (б)

 

В [2] анализируется обнаруживающая способность АСT на одиночную ошибку. В [10] результаты такого анализа распространяются на кратные ошибки произвольной кратности:

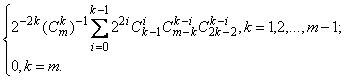             =            ( 1 )

На рис.6,а приведены графические зависимости вероятности, построенные по выражению (1) для различных значений . Графики показывают, что функцияявляется убывающей; максимальное значение она достигает при . При , близких к единице, значение  относительно велико, а при , близких к , - практически равно нулю. При небольших значениях () выражение (1) упрощается к виду

                                  ,  () ,                                              ( 2 )

На рис.6,б приведен график предельных значений, построенных по выражению (2)

 

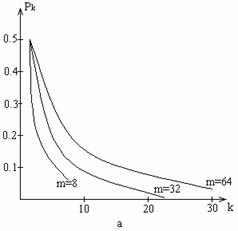
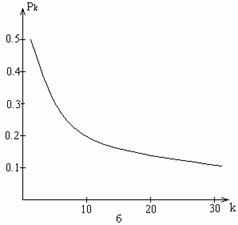
Рис.6 Вероятность необнаружения кратной ошибки:

а – график построен по формуле (1)

                                     б -- графикпостроен по формуле (2)

 

Анализ показывает, что для достаточно большого существует до 35 значений (), для которых .

Исследования выражений (1) и (2) позволяют оценить обнаруживающую способность одновходового АСА на кратные ошибки. Можно сделать следующие выводы:

 

§         с увеличением кратности ошибки повышается вероятность ее обнаружения, при этом наиболее "опасна" одиночная ошибка, вероятность обнаружения которой;

§         с ростом длины анализируемой последовательности вероятность обнаружения кратной ошибки уменьшается, стремясь к  некоторому пределу; для  такой предел определяется выражением (2);

§         диапазон наиболее неблагоприятных кратностей ошибок, когда вероятность необнаружения кратной ошибки превышает 10% (), лежит в пределах от  1 до  0.3, который при  может быть достаточно большим.

 

3. Расчет одиночной ошибки параллельного АСА

 

В предыдущей части статьи было показано, что наиболее "опасной" для одновходового АСА, как и для АСТ, является одиночная ошибка. Проведем расчет вероятности необнаружения такой ошибки для параллельных АСА.

 

При исследовании качественных характеристик анализатора обычно принимается дискретное представление тестовой реакции как последовательности двоичных -векторов, где - число выходов ОД (входов анализатора) [1-4]. Обозначим скалярные элементы анализируемой  и  эталонной ТР длиной   и разрядностью  как  и  , є {0,1}, є {0,1}, и представим ТР последовательностями векторов: ={}; ={}, а последние, в свою очередь, -- последовательностями соответствующих скалярных элементов: ={}; ={} , где i=1,2,…,m; j=1,2,…,r; m – длина (число векторов) ТР.

Длина m последовательностей при асинхронном анализе задается «аппроксимацией» , которая фактически определяет число изменений соседних векторов , удовлетворяющих некоторой функции, заложенной в УС анализатора [11].

Анализатор может обнаружить факт возникновения  неисправности ОД, если эта неисправность проявляется в его ТР, т.е., если  и отличаются значением хотя бы одного элемента. Поэтому, обозначив последовательность ошибок как ={E} , где E={e}, e{0,1}, взаимосвязь последовательностей ,  и  можно представить поразрядной суммой по "модулю два"[1-4]: . Последовательность  содержит ошибку,  если  e= 1 . Одиночная ошибка означает наличие в  Е  только одного такого элемента.

 

Рассмотрим произвольный сегмент  S -разрядной последовательности , состоящий из трех рядом расположенных векторов  W,,W, i=2,3,…,m-1. Пусть для векторов соответствующего сегмента последовательности ошибок  выполняются соотношения

Æ ,

E_i={ 00...010...00 }  Æ ,

т.е. крайние векторы сегмента неискажены (W=W, W=W), а вектор  отличается  от  W одним,  j-м,  j=1,2,...,r ,  разрядом  (= WЕ).

 

Суммарное число импульсов, вырабатываемых узлом УС при генерации сегмента Sдля линейного (N) и нелинейного (N) АСА можно рассчитать исходя из заложенной в нем функции аппроксимации [11] следующим образом:

,

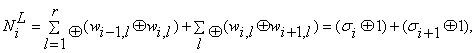
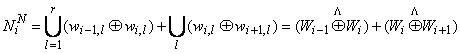где ;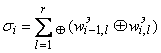

    - знак группового суммирования «по модулю 2»;

    «»- операция логического сложения поразрядной суммы «по модулю 2» скалярных элементов векторов :

 .

Ошибка E будет скомпенсирована, если  N (N)  будет равна соответствующему эталонному значению и не  изменится  вид  последовательности, сжимаемой РСЛОС. Для линейного АСА компенсация описывается следующими системами уравнений :

                            ;                  ,

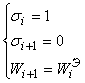каждое из которых выполняется на  22 из  2 всевозможных наборов. Тогда одиночная ошибка в сегменте S , а значит и во всей анализируемой последовательности  компенсируется линейным АСА с вероятностью

 

.

 

Для компенсации такой ошибки нелинейным АСА должны выполняться следующие системы уравнений:

;                     ,

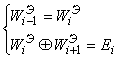каждая из которых выполняется на 2 из 2 всевозможных наборов. Поэтому

 

 

Если i=m, т.е. ошибка возникает в последнем векторе  входной последовательности, то она всегда будет обнаружена. Действительно, для линейного АСА такая ошибка приводит к изменению  мощности [11] , а для нелинейного АСА может привести к изменению мощности либо вида , что отразится на сигнатуре АСА. Поэтому в целом вероятность необнаружения одиночной ошибки линейными нелинейным АСА имеет следующие выражения:

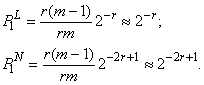
Анализ численных значений вероятностей, определенных по полученным выражениям:

 

	1	2	3	4	5	6	7	8
	0,5	0,25	0,125	0,0625	0,03125	1,56 x10-2	0,78 x10-2	0,391 x10-2
	0,5	0,125	0,03125	0,78 x10-2	0,2 x10-2	0,049 x10-2	0,012 x10-2	0,0031 x10-2

 

позволяют  сделать следующие выводы по обнаруживающей способности на одиночную ошибку:

 

§         с ростом разрядности АСА его обнаруживающая способность улучшается;

§         при фиксированной разрядности нелинейный АСА более эффективен, чем линейный;

§         линейный и нелинейный АСА разрядностью более 7 и 3 соответственно, обнаруживают одиночную ошибку с вероятностью более 99%; если же разрядность не меньше 8, то вероятность обнаружения одиночной ошибки оптимальным АСА практически равна 100% вне зависимости от типа анализатора.

 

 

Заключение

 

В представленной работе получены следующие основные  результаты

 

§         показано, что одновходовой АСА по «кратной» вероятности эквивалентен асинхронному счетчику и в целом характеризуется низкой обнаруживающей способностью для ошибок малой кратности. По этой причине его не рекомендуется применять для компактного анализа.

§         оптимальные ACA разрядностью более 8 обнаруживают одиночную ошибку с высокой вероятностью и поэтому могут успешно применяться для компактного анализа параллельных ТР;

§         наилучшей обнаруживающей способностью по кратной ошибке обладает нелинейный АСА, однако, он уступает линейному АСА по аппаратурным затратам;

§         полученные в статье результаты, а также общее свойство асинхронных счетных схем более эффективно обнаруживать ошибки малой кратности позволят выдвинуть гипотезу о том, что и АСА ведутся себя также. Подтверждение этой гипотезы нуждается в дальнейших исследованиях.

 

Литература

 

1.       Frohwerk R.A. Signature analisis: A new digital field service method // Hewlett Packard J. 1977, N 5,- p.2-8.

2.       Swith I.F. Measures of the effectivenes of fault signature analisis // IEEE Trans. on Compuf. 1980, N 6,- p.510-514.

3.       Кирьянов К.Г. К теории сигнатурного анализа // Техника средств связи. Сер. Радиоизмерительная техника. 1980, Вып.2. –с. 1-46.

4.       Ярмолик В.Н. Контроль и диагностика цифровых узлов ЭВМ. - Мн.: Наука и техника. 1988. - 240 с.

5.       Тупкало В.П. Основы теории сигнатурного анализа цифровых систем. Киев: Изд-во МО Украины, 1994. - 324c.

6.       Баран Е.Д. О достоверности контроля двоичных последователь­ностей методом счета состояний // Автоматика и вычислительная техника, 1982, N 6. -  с. 66-70.

7.       Fujiwara H., Kinoshita K. Testing logic circuits with compressed data // Digest of papers FTCS-8, 1978. -  p. 108-113.

8.       Hayes J.P. Transition count testing of combionational logic circuits // IEEE Trans. on Comput., 1976, N 6. - p. 613-620.

9.       Reddy S.M. A note on testing logic circuits by transition counting // IEEE Trans. on Comput., 1977, N 3. - p. 313-314.

10.   Зинченко Ю.Е. Исследование обнаруживающей способности асинхронного счетчика // Электронное  моделирование,1994, N2. - c.58-61.

11.   Зинченко Ю.Е. Компактное сжатие двоичных последовательностей асинхронным анализатором / Ред. журн. "Электронное моделирование". - Киев, 1988. -Деп. в ВИНИТИ 09.03.88. - 38с.

12.   Зинченко Ю.Е. Синтез оптимальных структур асинхронных сигнатурных анализаторов / Сборник трудов Донецкого государственного технического университета. Серия: Информатика, кибернетика и вычислительная техника,      выпуск 6. – Донецк: ДонГТУ, 1999.- С. 186-191.

13.   А.С.N1280634, МКИ G06F 11/00. Многоканальный сигнатурный анализатор                 / Зинченко Ю.Е.; Опубл. 30.12.87 Бюл. N48.

14.   А.С.N1383359, МКИ G06F 11/00. Многоканальный сигнатурный анализатор                 / Зинченко Ю.Е.; Опубл.23.08.88. Бюл. N11.

Назад в библиотеку.

URL: http://cs.donntu.ru/~zinchenk/art/ASAoptE1.rar

Первоисточник: Сборник трудов Донецкого государственного технического университета. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 10. - Донецк: ДонГТУ, 1999.- С. 282-288.