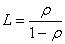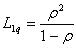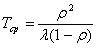Chernov Alexander Sergeevych

Faculty: Computing engineering and informatics

Speciality: Economic cybernetics

Theme of master's work: Markov’s models are in the economic queuing systems

Leader of work: Fel'dman Lev Petrovych

Email: 01_12_83@mail.ru

1. Introduction
2. Queuing systems
3. Conclusion

Introduction

The basic concepts of theory of the Markovskykh chains were entered by A.A. Markov in 1907. Since this theory was developed many conducting mathematicians. The important role of chains was lately revealed Markov in biological and sociological sciences. It is rotined that for the decision of all types of tasks it is enough to consider only two as the Markovskykh chains. Due to comparative simplicity and evidentness of mathematical vehicle, high authenticity and exactness of the got decisions, special attention the Markovskye processes were purchased at the specialists engaged in the operations analysis and theory of acceptance of optimum decisions. Practical application of theory of the Markovskykh chains requires knowledge of some terms and substantive provisions on which it is necessary to stop at exposition of examples. In many regions of practical activity of man we run into the necessity of stay in a state of expectation. Similar situations arise up in turns in booking-offices, in large air-ports, at expectation by the auxiliary personnel of airplanes of permission on flight or landing, at the public-call stations in expectant of liberation of line of subscriber, in repairs workshops in expectant of repair of machine-tools and equipment, on storages of procurement-sales organizations in expectant of unloading or loading of transports vehicles. In all transferred cases we deal with mass character and service. The theory of mass service is engaged in the study of such situations. In the theory of the queuing systems the served object is named the requirement. In general case under the requirement usually understand the request for satisfaction of some necessity, for example, talk with a subscriber, landing of airplane, purchase of ticket, receipt of materials on storage.

2. Queuing systems.

For the queuing systems characteristically presence of turn and stream of objects (homogeneous requirements). There are objects, requiring homogeneous service. It is the requirements or clients. The requirements form an incoming stream. Objects which serve, is named an attendant vehicle. Tasks of theory of mass service: adjusting by optimum appearance of turn, optimum organization of the queuing system. The second type of tasks is prognostications of conduct of the queuing system in different changing terms. The queuing systems can be unilinear and multilinear. In our example the system is unilinear, because only one vehicle works. The systems are odnofaznye and mnogofaznye. Our system is odnofaznaya. Graphicly the unilinear monophase model of mass service is represented so:

Every incoming stream of requirements is characterized by the middle closeness of receipt in time unit.[brows/mines]. The stream of requirements can be determined, the requirements enter strictly certain intervals of time and casual, which it is characterized by probability of receipt of number of requirements in unit of time , or probability of duration of interval between by the receipts of two neighbouring requirements : . The stream of requirements is external influence on the queuing system. Attendant a vehicle smears to serve every requirement or simultaneously group of requirements (service is individual or group). Time of service can be determined (permanent) and casual (meets most often). Probability of service is more frequent in all submits to the model law of probabilities distribution.

- mean time of maintenance of requirements.

- speed of service.

,where t - time, the requirement is served in the flow of which. Probability of appearance of n of requirements for t of time for a stream requirements formative simplest puassonovskyy stream, concernes on a formula: . Order of conduct of requirements in to the turn is named discipline turns. Incoming stream and time of service.

- probability of absence of requirements for t of time.

- probability of appearance of 1th requirement.

- probability of maintenance of one requirement for to time.

- probability of that for to time the requirement will not be served.

There is the unilinear monophase model of mass service, where ë is a middle fluence requirements; M is a parameter maintenances of one requirement; N is turn (maximally possible). We will consider time of t. As the system changes from t to t+ . E0 is event in the system the requirements are absent in the moment of time of t+ . Probability of events : in the moment of time of t is the requirement is absent complete group of events in the moment of time of t is one requirement. Complete probability of absences. , where Å1 – in the system there is one requirement during t of time. Ån – in the system is n requirement during t of time. Stationary probability is such probability which does not depend on time. Consequently, here Pn(t)=const, a P’n(t)=0. Adopting the terms of stationarity, we will define a load factor

Operating descriptions are those descriptions which influence at choice one or another queuing system (maximal length of turn, middle length of turn, maximal and mean time of finding, is in the system).

The middle number of requirement is in the system: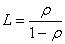

Dispersion or square of rejection of middle number of requirements:

Middle length of turn: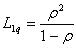

Mean time of expectation of service: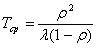

Maximal length of turn:

Conclusion

There is a question, it is how always possible to satisfy the economies of equilibrium to our models. Certainly, we are interested only by such economic systems which can really exist. It means that examined commodities (entrance) must be commodities which are somehow made and which can be made from nothing. Consequently, in every process must be expended at least one process productive this commodity. Considered examples it is possible substantially to improve, if to expect information taking into account the real terms.

At writing of this abstract of thesis, master's degree work is not yet completed. Final term of completion: January, 2007. Complete text of work and all materials on a theme can be got at an author or his leader - after the indicated date!!!