Источник: http://conf.bstu.ru/conf/docs/0030/0742.doc

Математическая модель процесса измельчения материала в ТШМ на основе теории систем массового обслуживания

Ломакин В.В., канд. техн. наук, доц.,

Ханин С.И., канд. техн. наук, доц.,

Трухачев С.С., аспирант

Белгородский государственный технологический

университет им. В.Г.Шухова

Современные рыночные отношения диктуют заводам необходимость применения систем автоматизации, что позволит качественно управлять технологическим процессом. Но для этого необходимо разрабатывать математические модели соответствующих процессов.

Предлагаемая математическая модель процесса измельчения позволяет рассчитывать требуемую длину камер, зависимость между количеством частиц материала, его гранулометрическим составом и количеством мелющих тел и их размерами в трубной шаровой мельнице (ТШМ), в которой осуществляются совмещенные процессы измельчения и классификации.  Отдельное мелющее тело в форме шара в системе массового обслуживания является обслуживающим прибором. Вблизи него в барабане мельницы имеется определенное количество материала, называемого требованиями на измельчение, составляющими очередь требований. Система массового обслуживания (СМО) представляет собой совокупность однолинейных систем с очередью по приоритетам и с отказами. Приоритет определяется размерами частиц материала.

Удовлетворение входного потока требований условиям стационарности, независимости воздействия и ординарности является предпосылкой пуассоновского потока заявок [1].

При совместном процессе измельчения-классификации наблюдается увеличение количества частиц материала совместно с удалением кондиционных частиц материала. В установившемся режиме за короткий промежуток времени работы мельницы можно принять равенство количества частиц, появившихся за счет разрушения, и количества частиц, выведенных из системы. Таким образом, имеем стационарный входной поток требований.

При допущении, что требование на измельчение одной частицы оказывает незначительное влияние на весь процесс измельчения в барабане мельницы для конкретного мелющего тела, так как количество подобных требований достаточно велико, выполняется условие независимости входного воздействия.

Выполнение условия ординарности определяется тем, что в очередь на обслуживание ставится только та частица материала, которая лежит в поле вектора скорости мелющего тела, а также тем, что очередь имеет приоритетную дисциплину.

Выполнение выше перечисленных условий позволяет сделать вывод о пуассоновском входящем потоке [1]. Вследствие чего функция распределения промежутков времени между последовательными поступлениями требований имеет вид

                                       (1)

с интенсивностью входящего потока  требований в секунду, средним промежутком времени между поступлениями  секунд и дисперсией .

Время обслуживания  задает промежутки от начала обслуживания до его завершения и может изменяться в зависимости от значения параметров при измельчении.  Время обслуживания представляет собой случайную величину, с определяющими параметрами: 1) величина математического ожидания ; 2) дисперсия .

Характеристикой процесса обслуживания является норма обслуживания  и интенсивность обслуживания .

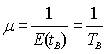,                                           (2)

где  - средняя продолжительность обслуживания.

Интенсивность обслуживания  определяется выражением

.                                              (3)

Средняя длина очереди определяется по формуле Полячека-Хинчина для среднего значения [2]

                                            (4)

Эта зависимость выражает среднюю длину очереди в момент ухода обслуженного требования через коэффициент использования ,  и  (второй момент распределения времени обслуживания).

Так как имеется система массового обслуживания с приоритетами, то будем разделять требования на соответствующие классы, где  - класс требования.

Среднее время ожидания  для требований из приоритетного класса p в случае СМО с относительным приоритетом обслуживания [2]:

 ,                       (5)

где , а .

Из этого выражения видно, что среднее время ожидание  не зависит от требований низших приоритетных классов иначе, как через числитель . Таким образом, зависимость (5) показывает, что  могут быть конечными (при , больших или равных некоторому критическому значению) и принимать нестабильные значения для низших приоритетных классов.

    В результате расчета математической модели измельчения в ТШМ были получены следующие важные зависимости: норма обслуживания (2), интенсивность обслуживания (3), средняя длина очереди (4), среднее время ожидания обслуживания для требований (5). Анализируя выражение (5), можно сделать вывод, что процесс измельчения в ТШМ эффективен до тех пор, пока частица материала не достигнет определенного размера. После чего, измельчению будут подвергаться частицы материала более крупного размера, и для оптимального измельчения по энергетическому критерию более мелкие частицы необходимо выводить из зоны измельчения, для чего необходимо применять классифицирующие внутримельничные устройства.

Список литературы

1.         Фритч В. Применение микропроцессоров в системах управления: Пер. с нем. – М.: Мир, 1984. - 464 с.

2.         Клейнрок Л. Теория массового обслуживания. Пер. с англ./Пер. И.И.Грушко; ред. В.И.Нейман. – М.: Машиностроение, 1979. – 432 с.