Источник: http://users.i.com.ua/~agp1/articles/hmm.pdf

Перевод: Чернов А.С.

Наблюдаемые Марковские Модели

Олег Головко, Алексей Пискунов

электронная почта: agp1@smtp.ru

2 мая, 2005

Аннотация. Эта статья представляет наблюдаемый образцовый эквивалент Скрытым Марковским Моделям. Модель не содержит скрытую часть и имеет такие же свойства как соответствующие СММ. НММ также направляются к некритическому и очевидному усовершенствованию в главных алгоритмах.

1 Введение

Мы будем использовать следующие понятия

Определение 1. Ориентированный граф G с параметрами (EG; V G), где

  . VG есть вызванный набор вершин и EG есть вызванный набор краев. Для любого края x =  означает .

Определение 2. I = [0; 1].

Определение 3. Вероятностное пространство - , где  есть  - алгебра подмножеств  ­ и P : F-> R есть вероятностная мера F ([2]).

Определение 4. Если  любой R или исчисляемый тогда P есть вызванное распределение вероятностей на  ([3]). Если  = R затем F F - Борелева алгебра на R, который уникален, если  исчисляется тогда F = 2 и поэтому определению  в этих случаях уникально определяет F и мы скажем этому P есть распределение вероятностей на .

Определение 5. Пуcть A будет графом вызванным первоначальным графом и B будет установлен из вызванного алфавита или демаскирующих признаков и VA есть распределения вероятностей  на B и  на .  есть вызванное распределение открытого для вершины  и  есть вызванное распределение перехода из вершины . Эти два набора распределений могли бы быть обработаны как функции b : V A * B -> I и a : V A*EA -> I соответственно. Функция i: V A -> R- распределение вероятностей на VA вызванное распределение начального состояния. Следование [1] под СММ, который мы поймем  = (a; b; i).

В переговорных системах признания обычно предполагается, что для первоначального графа V A =  и EA= ;

т.е. A является "цепным" с петлями на внутренних вершинах и i(v)= .

1.1 Скрытые Марковские Модели (СММ), основные алгоритмы

Есть 3 проблемы в СММ, но мы рассмотрим только #1 и #3 проблемы.

Пусть  и - открытая последовательность алфавита B,  - последовательность свойств.

Проблема #1. Считаем P , вероятность что предоставленная модель ¸ производит предоставленную последовательность OT.

Проблема #3. Регулируя модель ¸ для максимизации P для предоставленного OT .

Алгоритмы. Для решения проблемы #1 прямые и обратные алгоритмы могли бы использоваться, каждый требует  действия.

Прямой алгоритм. Означает вперед переменную , т.е. вероятность наблюдения последовательности  и в момент t состояние есть .

Решение.

Обратный алгоритм. Означает обратную переменную , т.е. вероятность наблюдения последовательности  и в момент t состояние есть .

Решение.

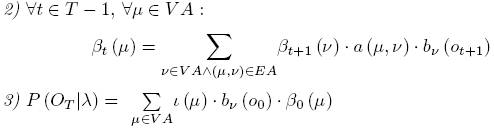
Решение проблемы #3, Баум-Велш алгоритм. Пусть

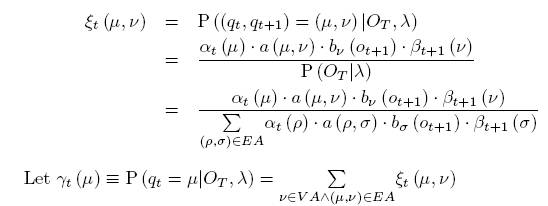
- ожидаемое число переходов от вершины ;

- ожидаемое число переходов над краем x.

Самая трудная часть решения - проблема минимизации, основные параметры:

Это могло бы быть сделано и в других отношениях, но точные алгоритмы не важны для нас сейчас.

2 Наблюдаемые Марковские Модели (НMM)

Определение 6. Для представленного СММ  определить модель OMM  с графом и функциями  и .  состав вершин V  = V A*B, вызванные состояниями, и края ,  определен, как  определен, как

 и  выдаст.

Очевидно граф  сложнее первоначального графа A, но общая модель

упрощается, потому что состоит из единого распределения вероятностей вместо двух, единый набор вершин вместо двух различных наборов вершин и

демаскирующих признаков.

Прямой алгоритм. Означает вперед переменную ,  т.е. вероятность наблюдения последовательности и в момент t состояние есть .

Решение.

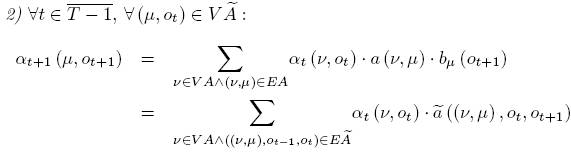
Считаем          это могло бы быть переписано как:

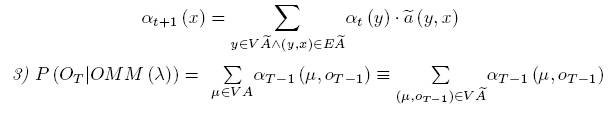
Обратный алгоритм. Означает обратную переменную  , т.е. вероятность наблюдения последовательности  и в момент t состояние есть .

Решение.

Считаем    это могло бы быть переписано:

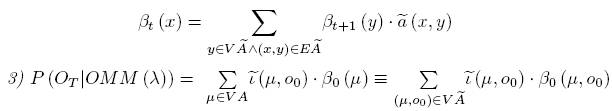
Решение проблемы #3, Баум-Велш алгоритм НMM.

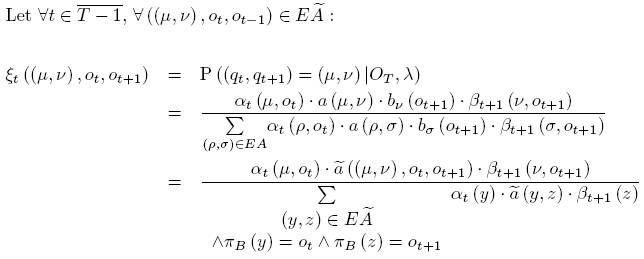
Считаем   и в сумме в знаменателе:  и , это могло бы быть переписано:

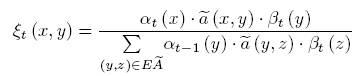
Конструкция OMM доказывает следующее утверждение.

Утверждение 1. Для каждых СMM  существуют OMM ( ) такие, что .

Это означает, что СMM не содержат никаких дополнительных особенностей и это скрытые участие могло бы быть принят во внимание конструкцией соответствующей НMM которая полностью открыта.

Заключение. Мы определили модель, которая эквивалентна СMM, но не содержит никакой скрытой части и единого распределения вероятностей вместо двух, которые появляются в СMM. Это позволяет переопределить СMM в более последовательном математическом пути и чтобы улучшить главные алгоритмы СMM, однако эти усовершенствования так тривиальны это вероятно находился во внимание во всех выполнениях во всяком случае. В то же время предложенная модель само собой стала меньше интуитивной и потеряла это прямое подсоединение к проблемам, которые получили это.

Список литературы.

[1] Lawrence R. Rabiner, "A Tutorial on Hidden Markov Models and Selected

Applications in Speech Recognition", Proceedings of the IEEE, vol.77, No.2,

February 1989, http://www.ai.mit.edu/~murphyk/Bayes/rabiner.pdf

[2] http://www.en.wikipedia.org/wiki/Probability theory

[3] http://www.en.wikipedia.org/wiki/Probability distribution

[4] Rakesh Dugad, U. B. Desai "A Tutorial on Hidden Markov Models",

http://www.uirvli.ai.uiuc.edu/dugad/hmm tut.html

[5] http://www.unisay.com