© Ф.Пинежанинов,
П.Пинежанинов
В начало
Зеркало: http://pinega.da.ru/
Метод конечных элементов используется при
решении многих практических задач и
поддерживается многими программными продуктами.
Цель этой статьи - снять завесу таинственности
с понятия конечного элемента, что, как надеются
авторы, приведет к более осмысленному их
использованию: не фетишизируя с одной стороны и
используя максимально их возможности с другой.
Пусть это поможет и изобретать новые
элементы, позволяющие более эффективно
справляться с возникающими проблемами. При
описании конечных элементов будем использовать
конструктивный, а не аксиоматический подход, как
более подходящий для поставленных целей.
Зададим нумерацию 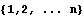 и, свяжем с ней
совокупность всевозможных семейств
действительных чисел и, свяжем с ней
совокупность всевозможных семейств
действительных чисел 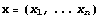 , которая после введения
операций покомпонентного сложения и умножения
на число будет n-мерным арифметическим линейным
пространством , которая после введения
операций покомпонентного сложения и умножения
на число будет n-мерным арифметическим линейным
пространством 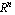 . .
После введения в 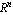 обычным образом
скалярного произведения обычным образом
скалярного произведения 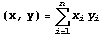 и нормы, им
определяемой, получим сепарабельное
Гильбертово пространство. В этом
пространстве существует ортонормированный
базис и нормы, им
определяемой, получим сепарабельное
Гильбертово пространство. В этом
пространстве существует ортонормированный
базис 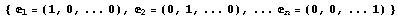 и каждую компоненту элемента из и каждую компоненту элемента из 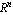 можно
единственным образом представить в виде
линейного функционала, определяемого скалярным
произведением можно
единственным образом представить в виде
линейного функционала, определяемого скалярным
произведением 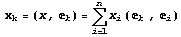 . Здесь . Здесь 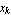 по существу коэффициенты
Фурье для ортонормированного базиса. по существу коэффициенты
Фурье для ортонормированного базиса.
С исходной нумерацией 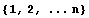 свяжем в трехмерном
геометрическом пространстве (вообще размерность
может быть любой) множество точек свяжем в трехмерном
геометрическом пространстве (вообще размерность
может быть любой) множество точек 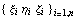 , называемых
узлами интерполяции или просто узлами. Через
исходную нумерацию узлы взаимооднозначно
связаны с , называемых
узлами интерполяции или просто узлами. Через
исходную нумерацию узлы взаимооднозначно
связаны с 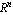 и
в дальнейшем можно считать x и и
в дальнейшем можно считать x и 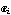 зависящими
или от узлов или от нумерации. зависящими
или от узлов или от нумерации.
Следовательно, линейный функционал 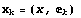 можно
записать в следующем виде: можно
записать в следующем виде: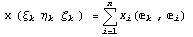 . Скалярное
произведение . Скалярное
произведение 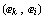 ,
это значение ,
это значение 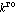 базисного вектора в базисного вектора в 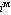 узле
или наоборот и его можно рассматривать как
функцию узле
или наоборот и его можно рассматривать как
функцию 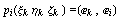 . .
С учетом этого линейный функционал можно
записать в виде 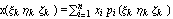 . .
Все это справедливо для множества узлов,
которое является подмножеством геометрического
пространства, и опираясь на теорему Хана -
Банаха о расширении линейного функционала, можем
записать 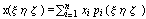 . .
Семейство функций 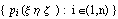 , в случае линейной
независимости своих элементов, образует базис
функционального пространства над
геометрическим пространством. , в случае линейной
независимости своих элементов, образует базис
функционального пространства над
геометрическим пространством.
Выражение 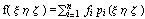 позволяет вычислить значение
функции f в любой точке геометрического
пространства по конечномерному арифметическому
семейству значений в узлах позволяет вычислить значение
функции f в любой точке геометрического
пространства по конечномерному арифметическому
семейству значений в узлах 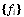 , то есть является
интерполяционной формулой, если известны
базисные функции. , то есть является
интерполяционной формулой, если известны
базисные функции.
Следуя объектно-ориентированному подходу,
дадим определение конечного элемента как
тройки семейств и правила вычисления -
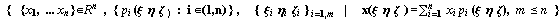
или словами:
{ степени
свободы, базисные
функции, узлы, интерполяционная
функция },
при этом будем подразумевать, что все объекты
удовлетворяют построению, изложенному выше. Пока
будем считать, что число базисных функций и
узлов совпадает, то есть n=m, - такие
элементы обычно называют Лаграгжевыми, а
обобщения на элементы, учитывающие
производные и композиционные элементы дадим
позднее.
Обычно для функционального пространства
несложно задать некоторый базис из n линейно
независимых функций, однако, его надо
преобразовать к такому - который удовлетворяет
выше приведенному построению.
Как это сделать ниже рассматривается на
полиномиальных базисах как наиболее
употребительных, что не снижает общности
предлагаемых технологий. Введенной нумерации 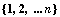 , для большей
общности всегда можно сопоставить другую
нумерацию , для большей
общности всегда можно сопоставить другую
нумерацию 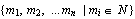 . .
В трехмерном пространстве, описываемом
координатами 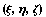 , для описания функций , для описания функций 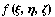 введем базис трехмерного
пространства введем базис трехмерного
пространства 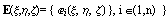 , содержащий n линейно
независимых функций. , содержащий n линейно
независимых функций.
Произвольную функцию 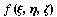 можно
описать через базисные функции в виде можно
описать через базисные функции в виде 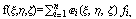 , где , где  - n степеней свободы
разложения функции по базису. - n степеней свободы
разложения функции по базису.
В трехмерном пространстве обозначим связную
область с помощью n точек - называемых
узлами элемента. Обычно область является
треугольником, четырехугольником возможно с
криволинейными границами на плоскости или их
пространственными аналогами в трехмерном
случае.
Далее рассмотрим, как зная базис
пространства и множество узлов элемента
построить множество базисных функций
ассоциированных с узлами и, при необходимости,
модифицировать с целью придания степеням
свободы определенных свойств. Для этого надо
построить матрицу преобразования из одного
базиса в другой.
Базис, связанный с конечным элементом  , можно записать через исходный базис
следующим образом , можно записать через исходный базис
следующим образом
 , где , где  -
координаты нового базиса в исходном базисе и
наша задача найти эти координаты. -
координаты нового базиса в исходном базисе и
наша задача найти эти координаты.
Из построения базисных функций известны их
значения в узлах 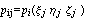 , значит можно
вычислить и значения полиномиального базиса в
этих же узлах , значит можно
вычислить и значения полиномиального базиса в
этих же узлах 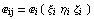 и, следовательно,
для i - базисной функции справедлива
запись и, следовательно,
для i - базисной функции справедлива
запись 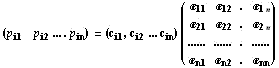 . .
Так как эта запись справедлива для каждого
узла, то, объединяя записи по всем узлам,
получим матричное уравнение
 в котором в левой части
матрица P значений базиса, связанного с конечным
элементом в его узлах (узел соответствует
столбцу) , C - матрица неизвестных
коэффициентов (по строкам координаты
конечноэлементного базиса в исходном для
пространства), E - матрица значений исходного
базиса(полиномиального) в узлах конечного
элемента (узел соответствует столбцу). в котором в левой части
матрица P значений базиса, связанного с конечным
элементом в его узлах (узел соответствует
столбцу) , C - матрица неизвестных
коэффициентов (по строкам координаты
конечноэлементного базиса в исходном для
пространства), E - матрица значений исходного
базиса(полиномиального) в узлах конечного
элемента (узел соответствует столбцу).
Таким образом, 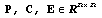 образуют
матричное уравнение образуют
матричное уравнение 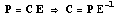 и
учитывая, что базисные функции элемента обычно
равны 1 в своем узле и 0 в остальных, а
следовательно P - единичная матрица, можем
записать и
учитывая, что базисные функции элемента обычно
равны 1 в своем узле и 0 в остальных, а
следовательно P - единичная матрица, можем
записать 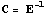 . Полученное
выражение позволяет легко получать базисные
функции в системе символьных вычислений "Mathematica"
Стивена Вольфрама, которой и будем пользоваться. . Полученное
выражение позволяет легко получать базисные
функции в системе символьных вычислений "Mathematica"
Стивена Вольфрама, которой и будем пользоваться.
Необходимость обращения матрицы значений
исходного базиса в узлах помимо обычного
требования линейной независимости базиса
накладывает и некоторые ограничения на выбор
узлов, так как столбцы матрицы E должны быть
линейно независимы, и, следовательно, узлы должны
быть по крайней мере различными.
Практически обычно используют
полиномиальный базис трехмерного пространства 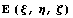 порядка N, полученный как
степени порядка N, полученный как
степени 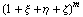 . Для примера: m=0,1,2,3,4 . Для примера: m=0,1,2,3,4
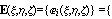
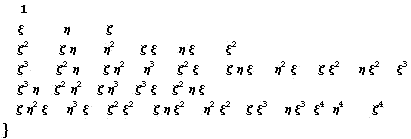 порядка 4,
содержащий n=35 базисных функций. порядка 4,
содержащий n=35 базисных функций.
В качестве примера, алгоритм построим для
треугольно-кубического элемента с внутренним
узлом. Он содержит 10 узлов поэтому базис
пространства возьмем из десяти полиномов не
содержащих 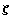 в порядке
возрастания степеней в порядке
возрастания степеней 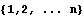
Построим и обратим матрицу, столбцы которой
- значения базисных функций пространства в узле
конечного элемента

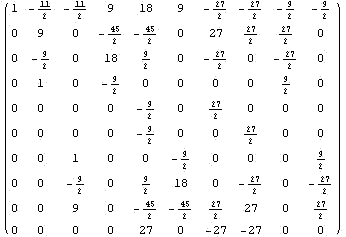
В методе конечных элементов обычно базисные
функции элемента были равны 1 в согласованном
узле и обращаются в 0 во всех остальных и,
следовательно, матрица желательных значений
будет единичной. Это позволяет сразу записать
базисные функции элемента, так как полученная
матрица по существу есть матрица коэффициентов
нового базиса в старом.
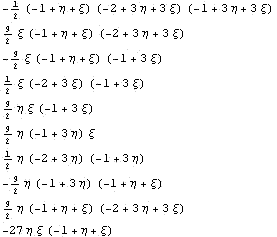
Полезно проверить, что сумма полученных
базисных функций для Лагранжевых элементов дает
единицу.
1
Иногда надо избавиться от внутренних узлов при
этом, для обратимости матрицы Ep, надо сократить
базис исходного пространства. Например, следуя
Стренгу и Фиксу, объединить базисные функции. При
этом надо учитывать, что аппроксимирующие
свойства полученного базиса для
модифицированного элемента естественно
понизятся. При этом если функции базиса
исходного пространства окажутся
линейно-зависимыми, то обратить матрицу их
значений в узлах, в силу ее вырожденности,
естественно не удастся. Так будет если
объединить 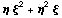 , но если
изменить знак, то все нормально: , но если
изменить знак, то все нормально:
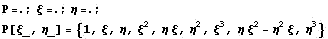

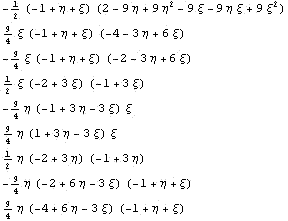
1
Выше описан 10 узловой конечный элемент от двух
переменных с внутренним узлом и возможный
вариант понижения его до 9 внешних узлов через
объединение в линейной комбинации элементов
полиномиального пространства.
Иногда, исходя из геометрических или
физических соображений, удобно понижать
размерность исходного пространства через
задание некоторых линейных условий на 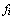 - степени свободы линейной интерполирующей
формы - степени свободы линейной интерполирующей
формы 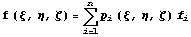 . .
Рассмотрим технологию такого преобразования.
Пусть исходное полиномиальное пространство и
число узлов согласованы, но мы хотим исключить
один узел предположив 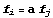 , тогда, желательные степени
свободы можно записать в виде вектора , тогда, желательные степени
свободы можно записать в виде вектора
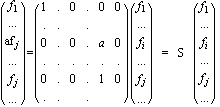 где матрица связи S почти
единичная за исключением строк связанных с
зависимыми степенями свободы, которые просто
заменяют зависимую степень свободы на
соответствующее линейное соотношение от
независимых степеней свободы. где матрица связи S почти
единичная за исключением строк связанных с
зависимыми степенями свободы, которые просто
заменяют зависимую степень свободы на
соответствующее линейное соотношение от
независимых степеней свободы.
Запишем линейную форму в матричном виде
учитывающем соотношение связи
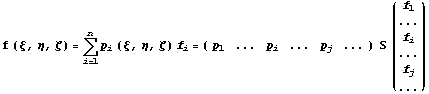 . Первые два
сомножителя можно рассматривать как
преобразование базиса с понижением количества
базисных функций так как i столбец, . Первые два
сомножителя можно рассматривать как
преобразование базиса с понижением количества
базисных функций так как i столбец,
соответствующий i зависимому узлу всегда
нулевой и, следовательно, согласованная с ним
базисная функция тождественный 0 и ее можно
опустить. Новый базис будет  . .
Практическое
применение этого подхода рассмотрим на примере
исключения внутреннего узла для
треугольно-кубического элемента. Сьярле и
Равьял предложили исключать внутренний узел,
определив его как линейную комбинацию внешних
узлов по следующему правилу 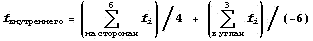 . .
Как обычно сначала строим полиномиальный базис
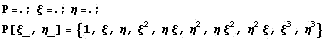
Затем строим базис конечного элемента с
внутренним узлом

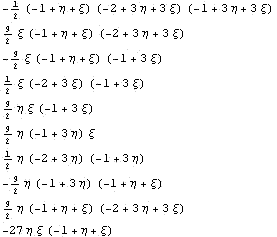
Строим матрицу связей в виде списка для
"Математики"

Умножением базиса элемента на матрицу связей
получаем новый базис для элемента без
внутреннего узла и проверяем, что сумма новых
базисных функций равна 1
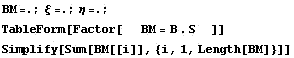
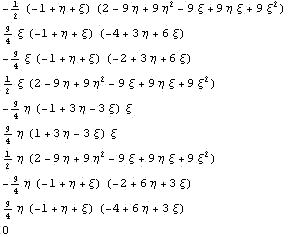
1
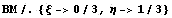
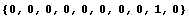
Несложно проверить, что коэффициенты перед
срединными и угловыми узлами удовлетворяют ниже
приведенному уравнению. Это уравнение позволяет
подобрать много различных пар коэффициентов,
которые позволяют исключать внутреннюю точку и
строить удовлетворительные базисные функции.
Почему надо предпочесть коэффициенты 4 и -6 для
авторов загадка.
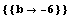
Ранее мы привели определение конечного
элемента как тройки семейств и правила
вычисления
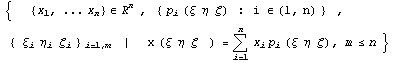
и считали m = n. Записывая базисные функции 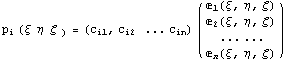 через исходный базис пространства и
опираясь на знание их значений в узлах через исходный базис пространства и
опираясь на знание их значений в узлах 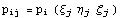 , мы получали уравнение для квадратных
матриц , мы получали уравнение для квадратных
матриц 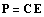 из решения
которого, находили неизвестные коэффициенты
конечноэлементного базиса, а следовательно и
сами базисные функции. из решения
которого, находили неизвестные коэффициенты
конечноэлементного базиса, а следовательно и
сами базисные функции.
Пусть m <n , тогда P и E будут прямоугольными
матрицами и, для разрешимости уравнения,
мы должны доопределить n-m соотношениями. Если
нам известны n-m значений некоторых производных в
узлах, то продифференцировав выражение для 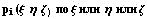 или направлению получим
соотношения для доопределения до квадратных
матриц, а следовательно и для определения
базисных функций , учитывающих информацию о
производных. или направлению получим
соотношения для доопределения до квадратных
матриц, а следовательно и для определения
базисных функций , учитывающих информацию о
производных.
Для примера, пусть известна информация о
производных в некоторых узлах 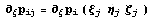 тогда тогда
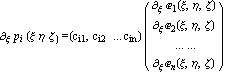 . .
Так если известна информация о соответствующих
производных во всех узлах, то получим
классические Эрмитовы конечные элементы. При
этом степеней свободы должно быть в 3 раза
больше чем узлов интерполяции для трехмерного
пространства.
Ниже приведен пример построения базисных
функций для двухузлового Эрмитова элемента
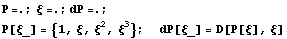
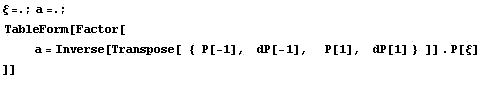
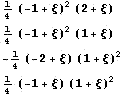

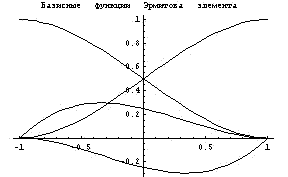
Еще пример элемента с производными по углам и
точкой в центре
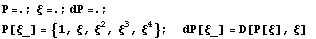
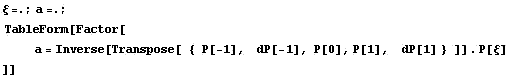
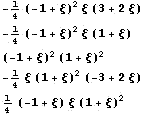
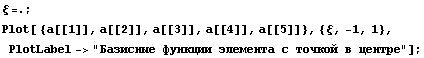
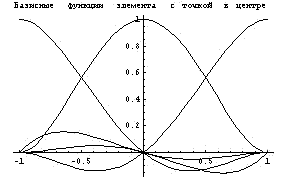
Для двухмерного пространства можно
использовать, например, такие элементы:
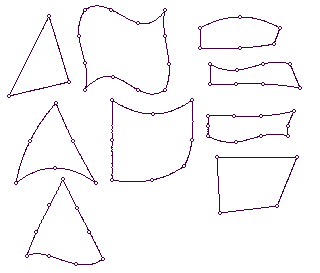
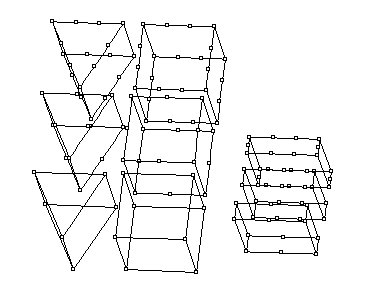
Для трехмерного пространства можно
использовать что-то похожее на эти элементы:
Приведенными изображениями не ограничиваются
возможности создания элементов.Обращаем ваше
внимание на то, как введение некоторых разумных
ограничений на область интерполяции
естественным образом порождает понятия о углах,
ребрах и гранях конечных элементов.
Наверное следовало бы еще написать о
изоморфизме конечных элементов, основываясь на
котором удобно интегрировать функции
определенные на них, о оценке интерполяционных
свойств базисных функций с помощью функции Series,
разлагающей в ряд Тейлора и дающей оценку
остаточного члена.
Полезно описать проверку взаимной
однозначности отображения одного элемента на
другой и построение линейных, поверхностных и
объемных элементов в  ,
стоило рассказать как с помощью линейного
функционала определить какую же область
пространства занимает конечный элемент. ,
стоило рассказать как с помощью линейного
функционала определить какую же область
пространства занимает конечный элемент.
Интересно было бы рассмотреть, как строить
специальные комбинированные элементы,
основанные на внедрении логических
операторов в понятие базисных функций, например,
для трещин или специальных геометрических форм.
Надо бы расcказать, как строить глобальную
матрицу и почему полезно использовать при этом
однородную систему, для ее модификации в
соответствии с краевыми условиями в виде
линейных связей.
Но об этом и многом другом в следующий раз по
мере поступления Ваших вопросов, поэтому следите
за публикациями.
- Дьяконов В.П. Системы символьной
математики Mathematica 2 и Mathematica 3: - М.: СКпресс,
1998.
- Колмогоров А.Н., Фомин С.В. Элементы
теории функций и функционального анализа: - М.:
Наука, 1981.
- Корнеев В.Г. Схемы метода конечных
элементов высоких порядков точности: - Л:
Изд.Лен.ун-та,1977.
- Лоран П.-Ж. Аппроксимация и
оптимизация: Пер. с франц. - М.: Мир, 1975.
- Митчелл Э., Уэйт Р. Метод конечных
элементов для уравнений с частными производными:
Пер. с англ. - М.: Мир, 1981.
- Стренг Г.,Фикс Дж. Теория метода
конечных элементов: Пер. с англ. - М.: Мир, 1977.
- Сьярле Ф. Метод конечных элементов для
эллиптических задач: Пер. с англ. - М.: Мир, 1980.
Санкт-Петербург, декабрь 1999
В начало |