Данная статья является тезисами к докладу на конференции "Компьютерный мониторинг и информацоинные технологии 2006", которая проходила в ДонНТУ 15 мая 2006 г.
АЛГОРИТМ ПОСТРОЕНИЯ ДЕРЕВЬЕВ РЕШЕНИЙ ДЛЯ СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ИЗВЛЕЧЕНИЯ ЗНАНИЙ
Чернов И.А., Федяев О.И.
Донецкий национальный технический университет
Рассматривается задача автоматического обнаружения знаний в реляционных базах данных, которая относится к проблеме интеллектуального анализа данных. Актуальность ее решения заключается в нахождении скрытых закономерностей в накопленных экспериментальных данных, позволяющих обобщить опыт и определить факторы, влияющие на достижение поставленной цели. Выявленные знания об объекте анализа можно использовать для повышения качества его управления.
Формально задача автоматического извлечения знаний из баз данных может быть описана следующим образом. Предметная область представляется в виде реляционной модели данных, которая описывается отношением R, являющимся подмножеством кортежей декартового произведения
| (1) |
где xi –значения входных атрибутов Xi из домена DXi; yi –значения выходных атрибутов Yi из домена DYi; P(x1,…,xn,y1,…,ym)– предикат, описывающий условия отображения конкретной предметной области в кортежи значений атрибутов < x1,…,xn,y1,…,ym>.
Необходимо сформировать отображение в виде набора правил
| {X1,X2,..,Xn}-> {Y1,Y2,…,Ym} | (2) |
ставящих каждому входному набору значений {xi=DXi, i=1..n} в соответствие некоторый набор целевых значений {yj=DYj, j=1..m}. Полученные функциональные зависимости
| Yj = Fj(X1,X2,….,Xn), j=1..m | (3) |
должны быть верны для кортежей отношения (1) и могут быть использованы при нахождении выходных атрибутов Yj для новых значений входных атрибутов Xi (i=1..n).
Для автоматизированного извлечения знаний использовался метод CART (classification and regression trees)[2] из класса методов деревьев решений. Данный подход является самым распространенным в настоящее время способом выявления, структурирования и графического представления логических закономерностей в данных. Его преимущества заключаются в следующем[2]:
Хорошая эволюция и достигнутый уровень формализации методов послужили основанием использовать процедуру CART, как лучший из этого класса, в блоке извлечения знаний. В данном алгоритме можно выделить три операции, от реализации которых зависит его трудоёмкость и качество обнаружения знаний: сортировка источника данных при формировании множества условий U для атрибутов числового типа, вычисление критерия Gini [2] при разбиении узлов бинарного дерева, перемещение в таблице значительных объёмов информации при делении узла.
Покажем вычислительные затраты при классификации одного узла дерева. Пусть узлу, для которого осуществляется классификация, соответствует M объектов (строк) сводной таблицы. Каждая строка таблицы рассматривается как один пример обучающей выборки. Параметром N обозначим количество атрибутов таблицы без учёта целевого атрибута. Предположим, что в базе данных содержатся только атрибуты категорийного типа, имеющие в среднем Ncp значений.
Для определения необходимости последующего деления узла потребуется M проверок. Рассмотрим случай, когда из узла порождаются узлы-потомки. В этом случае для каждого атрибута формируются 2Ncp-1-1 возможных условий ui принадлежит U (|U|=2Ncp-1-1) (4), которые определяют варианты разбиения узла. Эта операция реализуется M проверками. Отбор наилучшего варианта разбиения узла дерева проводится по наибольшей классифицирующей силе, вычисляемой по критерию Gini [2]:
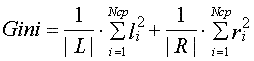 |
(5) |
Из формулы (5) видно, что её вычислительная сложность состоит из суммы следующих операций: подсчёт элементов li, ri класса i (i=1..Ncp) в множествах L и R и вычисление индекса Gini. Подсчёт объектов каждого класса занимает M операций, а вычисление индекса Gini выполняется за 2*Ncp+2 операций. Следовательно, классификация узла по условию ui и отбор наилучшего разбиения занимает в целом 2M + 2Ncp операций. Тогда для каждого категорийного атрибута потребуется (2M + 2Ncp)*( 2Ncp-1-1) операций. А так как таблица имеет N атрибутов, то классификация одного узла без учёта разделения будет занимать (2M + 2Ncp)*(2Ncp-1-1) *N +M условных операций. На примере таблицы, содержащей 1000 строк, 10 категорийных атрибутов с 5 возможными значениями, разбиение корневого узла дерева потребует приблизительно 300 000 условных операций, что значительно меньше полного перебора.
В качестве предметной области для проведения интеллектуального анализа рассмотрена медицинская диагностика. Часть данных (90%) использовалась для извлечения знаний, а остальные 10% - для оценки качества прогнозирования исходов лечения. При этом правильно было спрогнозировано 48 исходов лечения из 70. Для увеличения эффективности алгоритма планируется использование генетических алгоритмов для увеличение точности прогноза в узлах дерева содержащих небольшое количество элементов.
Литература
E-mail : iachernov@mail.ru