An abstract of a master's thesis
"Inventory management system simulation"

Introduction

1. Problem description

2. The price promotion

Conclusions

References

1. Problem description

The inventory control problem aims to reduce overhead costs without hurting sales. An inventory control system is an integrated package of software and hardware used in warehouse operations, and elsewhere, to monitor the quantity, location and status of inventory as well as the related shipping, receiving, picking and putaway processes.

A perishable inventory is one in which all the units of one material item remaining in stock will simultaneously lose their utility. The remaining units must be discarded if they have not yet been used after storage for a fixed period of time. Common examples of perishable inventories are fashion garments, blood, and foodstuffs.

The amount and level of inventory can be constructed via the recursion (1) and (2):



where x_ti – represents the amount of inventory of residuary age t in the system at the end of time unit t.
m – working life;
d – demand;
(a)⁺=max(0,a).

The total costs per unit time is give by:


where K – Fixed ordering cost per order;
C – Replenishment cost per unit;
G – Backorder cost per unit;
b – A fraction of the excess (unsatisfied) demand per replenishment cycle can be backordered;
q – Lost sales cost per unit;
W – Outdate cost per unit;
h – Holding cost per unit per unit time.

As the life of the item increases, the size of the state space also increases.
It is extremely difficult to obtain the optimal expected outdating for a long lifetime item. In fact, this requires solving a multi-dimensional program with corresponding quantities for various ages at the beginning of each period, which involves complex recursive computation.

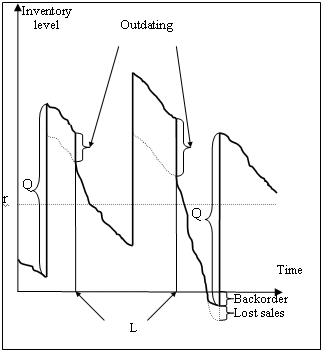
Three stockout cases in which customers or material users can choose to react to a stockout condition are considered. As previously stated, the three stockout cases are the full backorder, the full lost sales, and the partial backorder cases, which influence computation of the expected inventory levels per unit time and, then, the holding costs.

Figure 1 shows a (Q,r) perishable inventory model with a mixture of backorders and lost sales.


Figure 1
An approximate expected outdating of the current order size is given by:


where Q – order quantity;
r – Reorder point;
L – Positive order lead time;
F_m+L(u) – is the probability function of the random variable d_m+L.

An approximation of expected shortage quantity per cycle is given by:


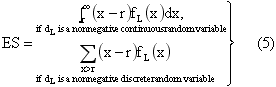
where f_L(x) – where is the probability function of the random variable d_L.

The approximation of the expected inventory level per unit time is given by:


The total expected average cost per unit time for the partial backorder case is given by:


where ET – Expected cycle length.

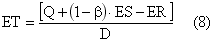
2. The price promotion

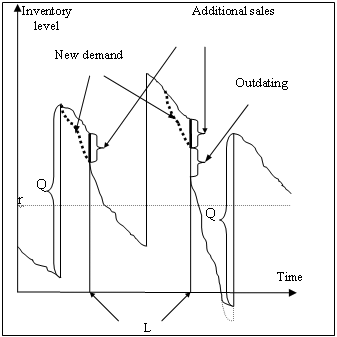
To maximize total reward, price promotions can be used to clear off the sale of items having less remaining useful life. In a price sensitive market price promotion can be a reasonable option to stimulate the demand.
There can be additional costs associated with the withdrawal of the promotion. A stochastic dynamic programming approach is used to maximize the expected reward over a finite horizon.

Figure 2 shows a (Q,r) perishable inventory model with a price promotion.


Figure 2
The algorithm for determinate an optimal time to announce price promotion and an optimal size of price promotion for a perishable item is given below.

Step 1. Determination of Q and r using an approximate equations (4) – (8).

Step 2. While (T_m – t) > M:
The goods are soled on an ordinary price.

Step 3. If (T_m – t) <= M: comparing U_t, and D(T_m – t):
– If U_t <= D(T_m – t) then
the price promotion dose not proposed, go to step 2;
– If Ut > D(T_m – t) then,
determination of price promotion size, go to step 4.

Step 4. i = T_m.
The expected reward is given by (9):
R(p, (T_m – t)) = p*min(U_t; D(p, (T_m – t))) – TCU•(T_m – t) (9)
While i <= t determine expected reward using (10):


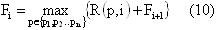
FT_m+1 = 0.

Step 5. Till the end of product useful time, the goods is sold with price promotion.

1. www.edpsciences.org/articles/ro/pdf/1999/01/ro3.pdf
   Huan Neng CHIU, “A Good Approximation of the Inventory Level in a (Q r) Perishable Inventory System”, Operations Research, vol. 33, ¹1, 1999, pp. 29-45.
2. W.L. Coopery and R.L. Tweediez, “Perfect Simulation of an Inventory Model for Perishable Products”, University of Minnesota, July 15, 2000.
3. www.iitb.ac.in/~ieor/nh/Revised-chande_paper.pdfA Chande, N Hemachandra and N Rangaraj. Fixed-life perishable inventory problem and approximation under price promotion // Technical Report, Industrial Engineering and Operations Research, Indian Institute of Technology Bombay, Mumbai, 2004.
4. www.ias.ac.in/sadhana/Pdf2005AprJun/Pe1304.pdf A Chandec, S Dhekane, N Hemachandra, N Rangaraj. Perishable inventory management and dynamic pricing using RFID technology // Industrial Engineering and Operations Research, Indian Institute of Technology, Bombay, Mumbai, Sadhana Vol. 30, Parts 2 & 3, April/June 2005, pp. 445–462.
5. Õåäëè Äæ., Óàéòèí Ò. Àíàëèç ñèñòåì óïðàâëåíèÿ çàïàñàìè. – Ì., «Íàóêà», 1969. – 511 ñ.
6. Ðûæèêîâ Þ. È. Òåîðèÿ î÷åðåäåé è óïðàâëåíèå çàïàñàìè: Ó÷åáíîå ïîñîáèå äëÿ âóçîâ. – ÑÏá.: Ïèòåð, 2001. – 384 ñ.
7. Õðóöêèé Å. À. Îïòèìèçàöèÿ õîçÿéñòâåííûõ ñâÿçóé è ìàòåðèàëüíûõ çàïàñîâ (Âîïðîñû ìåòîäîëîãèè). – Ì.: Ýêîíîìèêà, 1997. – 263 ñ.
8. Áóêàí Äæ., Êåíèãñáåðã Ý. Íàó÷íîå óïðàâëåíèå çàïàñàìè. – Ì.: Íàóêà, 1967. – 423 ñ.
9. David K. Smith. Dynamic Programming and Inventory Management: What Has Been Learnt in the Last Generation? // School of Mathematical Sciences University of Exeter, Exeter EX4 4QE, UK, 2000.