Моделирование системы управления запасами скоропортящихся товаров
I. ВВЕДЕНИЕ
Актуальность данной системы обусловлена необходимостью повышения конкуренции в сфере розничной торговли, что невозможно без создания, освоения и внедрения соответствующих инструментов для решения экономических задач. Поскольку малые и средние предприятия зачастую ограничены в денежных средствах, актуальной является разработка систем, автоматизирующих отдельные аспекты работы предприятия.
К одним из таких инструментов относятся автоматизированная система учета товаров на складе и система управления запасами. Зачастую планирование пополнения запасов необоснованно ведется по некоторым жестко установленным нормативам, независимо от того, насколько экономически оправдан данный уровень запаса в данной конкретной ситуации. Такой подход приводит к заведомо завышенному уровню запасов, что означает неоправданное отвлечение финансовых ресурсов и снижение их оборачиваемости [5]. Поэтому автоматизированная система управления запасами предприятия с одной стороны, не является слишком дорогостоящей, а с другой, может значительно повысить эффективность работы предприятия.
При наличии автоматизированной системы учета, система управления запасами должна основываться на модели управления запасами с постоянным контролем уровня запаса, т.е. система, в которой каждый раз, когда уровень запаса опускается до r, подается заявка на заказ размером Q.
II. ТОЧНОЕ УПРАВЛЕНИЕ СКОРОПОРТЯЩИМИСЯ ЗАПАСАМИ
Скоропортящийся запас - это запас в котором все единицы одного товара, оставшиеся на складе, одновременно потеряют свою полезность. Оставшиеся единицы должны быть выброшены, если они еще не были использованы после хранения в течение фиксированного промежутка времени. Поэтому управление запасами скоропортящихся товаров происходи следующим образом:
1) определяется оптимальный размер заказа (с учетом расходов на хранение, на дефицит и списание устаревших товаров) и подается заказ на пополнения запаса;
2) весь прибывший продукт считается новым;
3) отпуск товара производится по принципу «первый пришел – первый вышел»;
4) продукт, не реализованный в течение срока хранения, m, списывается.
Состояние запаса представляется вектором из m–1 компоненты (наличие продукта с распределением по оставшимся срокам годности в периодах) [4].
Для точного описания наличного запаса в каждый момент времени используется следующая формула [3]:

 – количество запаса возраста i в момент времени n;
– количество запаса возраста i в момент времени n;Dn – спрос в момент времени n.
III. ПРИБЛИЖЕННОЕ ОПИСАНИЕ МОДЕЛИ УПРАВЛЕНИЯ СКОРОПОРТЯЩИМИСЯ ЗАПАСАМИ
Использование формулы (1) при создании программного продукта, предназначенного для решения реальных задач управления запасами, практически невозможно, в связи со значительной вычислительной сложностью, вызванной использованием данной формулы. Поэтому в рассматриваемой системе используется приближенный подход для описания наличного запаса в каждый момент времени.
При формировании приближенного значения уровня запаса в каждый момент времени, используются следующие предположения:
1) запас покидает систему либо для удовлетворения спроса, либо изымается как устаревший товар;
2) часть неудовлетворенного спроса в системе задалживается, а часть – теряется безвозвратно, причем, доля задолженного спроса не меняется в зависимости от продолжительности дефицита.
В случае с полной потерей продаж весь неудовлетворенный спрос полностью теряется, и покупатели обращаются для удовлетворения потребности в товаре к другим источникам. Однако, часто возникает ситуация, когда при отсутствии на складе товара, некоторые покупатели ждут, пока не будет удовлетворен их спрос из следующего заказа. Таким образом, разумно предположить, что только часть дефицита, b (0<=b<=1), становится на учет, а остальная часть, (1–b), теряется навсегда. Динамика уровня запаса в такой системе изображена на рисунке 1.
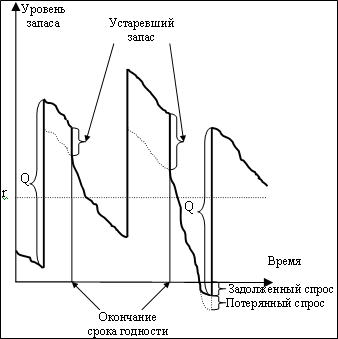
Ожидаемый уровень запасов в системе в любой момент времени можно описать соотношением (2) [2]:
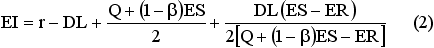
где EI – ожидаемый уровень запаса в единицу времени;
r – точка заказа;
DL – спрос во время доставки;
Q – размер заказа;
b – доля неудовлетворенного спроса в цикле пополнения, которая может быть задолжена;
ES – ожидаемый объем дефицита в цикле;
ER – ожидаемое количество устаревших товаров в текущем заказе размера Q.
В качестве приближения ожидаемого количества устаревших товаров в разрабатываемой системе используется соотношение (3):
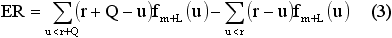
где fm+L(u) – вероятностная функция случайной переменной dm+L (т.е. спрос в течение m+L единиц времени).
Для описания ожидаемого размера дефицита используется соотношение (4):

где функция fL(x) – это вероятностная функция случайной переменной dL – спроса во время поставки заказа.
Оптимальная политика управления запасами, т.е. значения параметров Q и r, определяются из минимума общих затрат в единицу времени. Общие ожидаемые средние затраты в единицу времени для случая с частичным учетом неудовлетворенных требований можно определить из соотношения (5):
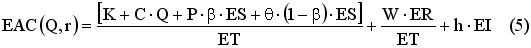
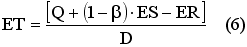
где K – фиксированные затраты на оформление заказа;
C – затраты на пополнение единицы запаса;
P – затраты, связанные с учетом неудовлетворенного спроса (за единицу);
q – затраты, связанные потерей неудовлетворенного спроса (за единицу);
W – затраты, понесенные вследствие устаревания товара (за единицу);
h – затраты на содержание единицы запаса в единицу времени;
ET – ожидаемая длина цикла, определяется из соотношения (6);
ER определяется из соотношения (3), ES – из соотношения (4).
В одном крайнем случае, когда b=0, случай с частичным учетом неудовлетворенных требований преобразуется в случай с полной потерей продаж, а в другом, когда b=1 – в случай с полным учетом неудовлетворенных требований.
IV. ВВЕДЕНИЕ СКИДКИ НА ПРОДАЖНУЮ ЦЕНУ ТОВАРА
4.1. СКИДКА ДЛЯ СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ ПРОВЕРКАМИ УРОВНЯ ЗАПАСА
Чтобы уменьшить объем устаревших запасов, которые подлежат списанию, в [1] предлагается ввести скидку на продажную цену продукции с целью повышения спроса, а, следовательно, уменьшения объема продукции, подлежащей списанию. Алгоритм определения скидки, описанный в [1], определяет оптимальный размер заказа и оптимальную ценовую политику для системы с периодическим контролем уровня запаса. В такой системе периодически (раз в день, неделю, месяц) проверяется наличный запас и, если он опустился ниже заданного уровня, делается заказ на Q единиц.
Рассматривается только один вариант скидки, при этом предполагается, что спрос известен как для случая, когда скидка используется, так и для случая продаж по обычной цене.
Целью задачи является определение оптимального размера заказа и времени введения скидки. Оптимальный объем заказа выбирается из диапазона от 0 до заказа, который в сумме с остатком на начало периода давал бы максимальный запас.
Поиск оптимальных параметров представляет собой задачу динамической оптимизации. Функция цели состоит в том, чтобы максимизировать общий ожидаемый выигрыш, Qt(st (a, yt)), для состояния st полученный за время от текущего состояния t до конца горизонта планирования, и зависящий от решения принятого в отношении ценовой политики, a, и объема заказа yt. Параметр a принимает значение p или n, в зависимости от того, вводится скидка или нет. Выигрыш, r(st (a, yt)), определяется как разница между доходом и затратами. Затраты включают:
– затраты на хранение запаса;
– затраты, понесенные вследствие дефицита;
– затраты на оформление и приобретение заказа;
– затраты, возникающие в связи с устареванием товара;
– затраты на введение ценовой скидки.
Выигрыш определяется по формулам (7) и (8) для случая с введением скидки и без введения скидки:
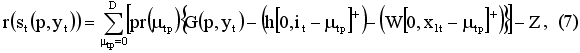
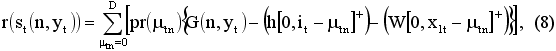
где mta – случайная переменная спроса в периоде t с известным распределением;
pr(mta) – вероятность того, что спрос в периоде t, при ценовой политике a будет равен mta;
it – общий запас в наличии в начале периода t;
xit – количество запасов в периоде t с оставшимся сроком использования i;
G(a, yt) определяется из соотношения (9):
где Ra – продажная цена;
[a, b]+ – максимум из (a, b), [a, b]– – минимум из (a,b).
В случае, если на этапе t было принято решение о введении ценовой скидки, то на всех последующих этапах рассчитывается только формула (7).
На последнем этапе затраты на содержание запаса отсутствуют, поэтому, ожидаемый выигрыш для случаев со скидкой и без определяется из соотношений (10) и (11) соответственно:
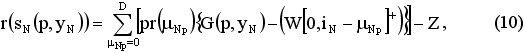
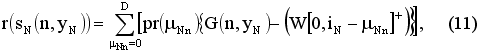
Общий ожидаемый выигрыш определяется по схеме (12):
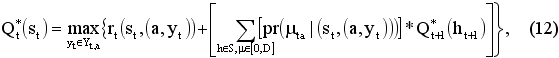
где Yt = {0…I – jt} – набор возможных значений для yt, I определяет максимальный запас, а jt – начальный запас, который переносится из предыдущего периода;
ht+1 – результирующее состояние в периоде (t+1);
pr(mta|(st, (a, yt))) – вероятность спроса mta в случае реализации действия (a, yt) в состоянии st в периоде t.
Оптимальная политика находится с помощью рекурсивной динамической процедуры, начиная с t = N и решая уравнение (12) пока t не станет равным нулю [1].
4.2. СКИДКА ДЛЯ СИСТЕМЫ С ОПЕРАТИВНОЙ ИНФОРМАЦИЕЙ ОБ УРОВНЕ ЗАПАСА
Рассмотрим основные условия использования скидки в рассматриваемой (Q, r)-системе управления запасами скоропортящихся товаров:
1) Скидка может быть установлена не на всем интервале срока годности товара (0…m), а только за определенное количество дней, М, до окончания срока использования товара.
2) Скидка устанавливается только в том случае, если за M дней до окончания срока годности товара, Tm, его объем на складе превышает ожидаемый объем продаж в течение M дней при текущем спросе. Действие такой скидки можно увидеть на рисунке 2.
3) Оптимальный размер заказа не зависит от устанавливаемой скидки.
4) Кроме определения времени установления скидки, система предусматривает определения ее величины. Оптимизация проводится по нескольким заранее установленным значениям скидок (например, p1 = 5%, p2 = 10%, p3 = 15%, p4 = 20%, …).
5) Спрос на товар при различных значениях скидки известен.
Следует обратить внимание на то, что скидка не всегда является экономически целесообразной. В некоторых случаях затраты на введение скидки могут превысить затраты, возникающие в связи со списание товара, срок годности которого истек. Например, при небольшом ожидаемом стоимостном объеме устаревших товаров, выгода, полученная при реализации товара со скидкой, может не покрыть расходы, понесенные в связи с введением скидки (внесение изменений в информационную систему, замена ценников, дополнительная работа сотрудников и др.).
Также, важно отметить, что целью введения скидки является не уменьшение объема списываемых в связи с устареванием товара запасов, а максимизация прибыли от реализации товара. Поэтому мы выбираем на ту скидку, при которой будет распродан весь товар, а ту, которая обеспечит максимальную выгоду. Это приводит к возникновению случаев, когда не весь объем товара будет реализован по истечении срока годности, а только его часть.
Ситуации с полной и частичной реализацией товара благодаря введению скидки изображены на рисунке 2.

Алгоритм работы системы можно представить следующим образом:
1) Пока (Tm – t) < M, каждый раз, когда уровень запаса в системе опускается до r, производится заказ, объемом Q. Q определяется исходя из минимума средних ожидаемых издержек в единицу времени, определяемых соотношением (5). Товар продается по обычной цене.
2) Если (Tm – t) >= M, то выполняется сравнение наличного запаса, Ut, и D(Tm – t) – ожидаемого объема реализации товара за время (Tm – t):
– если Ut <= D(Tm – t), скидка не предлагается, возвращаемся к шагу 1;
– если Ut > D(Tm – t), необходимо определить размер скидки, переходим к шагу 3.
3) Полагаем i = Tmm.
Прибыль за период времени i, R(p, i), полученная при установлении скидки p = {p1, p2,…pn} определяется соотношением (13):
где D(p, i) – спрос товар со скидкой p за период времени i;
EACp – определяется соотношениями (2), (3), (4), (5) с учетом нового значения спроса.
Ожидаемая прибыль за период от t до Tm определяется формулой (14):
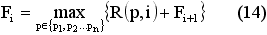
где Fi+1 – оптимальное решение на предыдущем этапе. FTm+1 = 0.
Итерации продолжаются, пока i не станет равным t.
4) До истечения срока годности товар продается со скидкой, установленной на шаге 3.
VII. ВЫВОДЫ
В данной работе быта рассмотрена (Q, r)-система управления скоропортящимся товарами. Данная система основана на приближенном описании ее ожидаемых параметров.
Однако, в связи со случайным характером спроса, определение ожидаемого уровня запаса в системе и затем, оптимальных параметров системы (размера заказа и точки заказа) будет неточным. Тогда возможна ситуация, когда на складе остается нераспроданный товар с истекшим сроком годности и подлежащий списанию. В такой ситуации предприятие будет неизбежно нести убытки, определяемые стоимостью просроченных товаров и затратами на их списание.
Чтобы уменьшить такие убытки в разрабатываемой системе вводится скидка на продажную цену продукции. Возросший в результате снижения цены спрос, будет поглощать излишек запасов и уменьшит объем списываемой продукции. Кроме того, в зависимости от объема излишков, возможен выбор оптимального размера скидки, а также времени ее внедрения.
ССЫЛКИ
[1] A Chande, N Hemachandra and N Rangaraj, “Fixed Life Perishable Inventory Problem and Approximation under Price Promotion”, Industrial Engineering and Operations Research Programme, IIT Bombay, Mumbai, India.
[2] Huan Neng CHIU, Shunji OSAKI “A Good Approximation of the Inventory Level in a (Q r) Perishable Inventory System”, Operations Research, vol. 33, №1, 1999, pp. 29-45.
[3] W.L. Coopery and R.L. Tweediez, “Perfect Simulation of an Inventory Model for Perishable Products”, University of Minnesota, July 15, 2000.
[4] Рыжиков Ю. И. Теория очередей и управление запасами: Учебное пособие для вузов. – СПб.: Питер, 2001. – 384 с.
[5] www.cs.comizdat.com Черненко М. Проблемы управления украинскими предприятиями. // Корпоративные системы, 2002, № 4.