Хорошее приближение уровня запасов в (Q, r) системе управления скоропортящимися запасами
1. Введение
Изучению определения оптимальной или лучшей политики заказов для скоропортящихся или устаревающих товаров уделялось значительное внимание в последние три десятилетия. Всесторонний обзор этой области можно найти в [13] и в [17]. Обычно, товары, имеющие ограниченный срок жизни являются результатом порчи или разрушения. Скоропортящийся запас – это запас в котором все единицы одного материала, оставшиеся на складе, одновременно потеряют свою полезность. Оставшиеся единицы должны быть выброшены, если они еще не были использованы (детерминированный или случайный спрос) после хранения в течение фиксированного промежутка времени. Распространенные примеры скоропортящихся запасов – это модная одежда, кровь, продукты питания. С другой стороны, ухудшающиеся или портящиеся запасы, как правило, имеют случайный срок жизни. Они могут быть определены как запасы, в которых часть оставшегося на складе материала теряет свою полезность (например, радиоактивные материалы, бензин) или запас, полезность каждого элемента которого уменьшается со временем (например, фрукты, овощи).
Эта статья сфокусирована на рассмотрении (Q, r) (объем заказа / точка перезаказа) оперативной системы управления запасами скоропортящихся товаров. Большинство предыдущих исследований [2, 4, 11, 12, 14] были сосредоточены на системах с периодическими проверками, неограниченным сроком жизни товара и нулевым временем выполнения заказа. Значительные усилия были потрачены на развитие хорошей аппроксимации точно ожидаемого количества устаревающих товаров (т.е. ожидаемое количество единиц определенного запаса в течение интервала времени). Это связано с тем, что крайне сложно получить оптимальное ожидаемое количество устаревающих товаров для предметов с длительным сроком жизни. Фактически, это требует решения многомерной программы с соответствующими количествами запасов различных возрастов в начале каждого периода, а потому включает множество рекурсивных вычислений. Насколько нам известно, в нескольких статьях рассматривалась (Q, r) оперативная система управления запасами скоропортящихся товаров, и, как известно, стала неразрешимой проблемой. [20] комментировал, что проблема скоропортящихся запасов становится крайне сложной при введении положительного времени доставки. Сложность состоит в том, что порча может применяться только к элементам в наличии, но не к тем, которые заказаны.
Недавно [3] разработал простую, но хорошую аппроксимацию ожидаемому уровню устаревших товаров для (Q, r) модели управления запасами скоропортящихся товаров с фиксированным сроком жизни и положительным сроком реализации заказа. Этот автор использует крайне грубое приближение ожидаемого уровня запасов в единицу времени, т.к. игнорирует при его вычислении ожидаемый уровень устаревших товаров в общем объеме заказа и ожидаемый объем дефицита за цикл. Хотя такое сильное предположение может упростить вычисление затрат на хранение, может возникать искажение в определении наилучшей политики определения объема заказа. [1] также показывает, что ошибка, возникающая при размещении заказа, связана не только с ошибочным размером партии, но и с функцией затрат на хранение. Поэтому вывод хорошей аппроксимации функции уровня запаса для сведения к минимуму искажения размера партии и штрафа является целью данного исследования.
Литература по (Q, r)-системе управления запасами со случайным спросом включает классическую (Q, r)-модель, представленную Хедли и Уайтином [6]. Они обсуждают случай с учетом и потерей неудовлетворенных требований при предположении, что порча товаров не допускается. Оптимальная политика состоит в размещении заказа размером Q единиц в момент, когда уровень запасов (наличные плюс заказанные) достигают точки перезаказа. [22] классифицировал проблемы управления запасами по огромному количеству схем исследований. Рассмотрение (Q, r)-системы со случайным спросом во время поставки, дефицитом и сроком годности элементов представляет особый интерес. Он обратил внимание, что для описания спроса во время доставки обычно используются нормальное распределение, гамма-распределение и распределение Пуассона. Однако всегда остается маленькая вероятность того, что спрос во время поставки будет отрицательным, когда для его описания используется нормальное распределение. В этом случае рекомендуется использовать усеченное нормальное распределения, но это может усложнить вычисления. Позднее, [5] представил (Q, r)-модель с пропорциональным времени учетом неудовлетворенных требований. Несколько (Q, r)-моделей со смешенным учетом неудовлетворенных требований и их потерей были предложены [16, 10, 9, 19, 15, 7]. Практически все предыдущие исследования использовали b – долю неудовлетворенного спроса, который ставился на учет (оставшаяся доля 1– b – полная потеря требований), для моделирования частично задолженного спроса. Недавно [18] смоделировал (Q, r)-систему используя управляющую переменную, которая ограничивает максимальное число учтенных требований, которые разрешается накапливать в течение цикла. Эти исследования не учитывали при построении модели предположение об ограниченном сроке хранения товара.
Вообще, издержками дефицита можно полагать независимые от времени издержки отсутствия запасов ($/единица), пропорциональные времени издержки дефицита ($/продолжительность отсутствия запасов/единица) или издержки отсутствия запасов за время простоя. Взвешенные во времени издержки дефицита пропорциональны продолжительности отсутствия запасов. С одной стороны, если издержки дефицита основаны на простое, то, согласно [23], простой может быть определен как время отсутствия запасов, не обращая внимания на количество единиц, отсутствующих на складе в течение цикла пополнения запасов. В этой статье рассматриваются три основных случая дефицита, при которых покупатели или потребители материалов могут выбирать, как реагировать на условия отсутствия запасов. Как было ранее установлено, три случая дефицита: с полным учетом неудовлетворенных требований, с частичным учетом и случай с полной потерей неудовлетворенных требований влияют на вычисление ожидаемого уровня запасов в единицу времени и на затраты содержания запасов. Здесь мы предположим, что ни случай полного учета неудовлетворенных требований, ни полной потери не зависят от продолжительности отсутствия запасов. В дополнение, другие допущения: случайный спрос, фиксированный срок жизни товара, b доля задолженного спроса и отсутствие оптовых скидок.
В этой статье мы рассмотрим три существующих приближения и выведем новое – для аппроксимации ожидаемого уровня запасов в единицу времени:
(1) Крайне грубая аппроксимация [3, 6].
(2) Аппроксимация без учета продолжительности дефицита и устаревания товара, предложенная [24].
(3) Аппроксимация с учетом продолжительности дефицита, но исключающая устаревание товара, предложенная [7].
(4) Хорошее приближение, основанное на нашем приближении ожидаемого уровня устаревших товаров [3], изложенная в этом исследовании.
2. Описание задачи
В этой статье рассматривается только один скоропортящийся продукт. Каждая единица продукта имеет фиксированный срок жизни m. Уровень запаса отслеживается постоянно и уменьшается за счет удовлетворения спроса или избавления от устаревших единиц. Заказ размером Q размещается, когда уровень запаса достигает точки перезаказа r. Существует положительное время доставки L для каждого пополнения и фиксированные затраты на оформление заказа K. Все единицы заказа на пополнение запаса прибывают свежими или новыми. Полезность каждой единицы товара не уменьшается и не исчезает до момента окончания срока годности, но товар должен быть выброшен, если он не был использован до истечения срока хранения. Затраты, понесенные вследствие устаревания товара равны W за единицу. Спрос в единицу времени, d1, – положительная случайная переменная. Предположим, что она имеет особое непрерывное или дискретное распределение с функцией плотности f1(y) = dPr{d1<=y}/dy и матожиданием D. Мы также предположим, что если N(t) – накопленный спрос ко времени t, то N(t) – случайный процесс со стационарными независимыми приращениями. Это подразумевает, что N(m) имеет плотность fm(z) = dPr{dm<=z}/dz и матожидание mD. Другими словами, N(m+L) имеет плотность fm+L(u) = dPr{dm+L<=u}/dy и матожидание (m+L)D. Единицы запаса всегда используются согласно FIFO политике выпуска (первый попавший на склад потребляется первым).
Условные обозначения, используемые в этой статье определены следующим образом:
Q – размер заказа
r – точка перезаказа
m – фиксированный срок использования скоропортящихся изделий
L – положительное время выполнения заказа
dL – спрос во время доставки с вероятностной функцией fL(x) = dPr{dL<=x}/dx и матожиданием LD, где FL(x) – это L-кратная свертка f1(y).
C – затраты на пополнение единицы запаса.
h – затраты на содержание единицы запаса в единицу времени.
K – фиксированные затраты на оформление заказа.
W – затраты, понесенные вследствие устаревания товара (за единицу).
P – затраты, связанные с учетом неудовлетворенного спроса (за единицу).
q – затраты, связанные потерей неудовлетворенного спроса (за единицу).
b – доля неудовлетворенного спроса в цикле пополнения, которая может быть задолжена, и оставшаяся доля 1–b – потеряна.
ET – ожидаемая длина цикла
EI – ожидаемый уровень запаса в единицу времени
ER – ожидаемое количество устаревших товаров в текущем заказе размера Q
ES – ожидаемый объем дефицита в цикле.
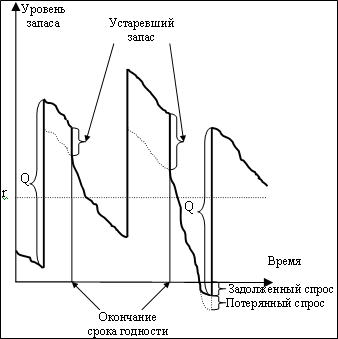
Рисунок 1 представляет (Q,r) модель запаса скоропортящихся товаров с задолженным и потерянным спросом.
3. Аппроксимация ожидаемой доли устаревших товаров по Chiu
Как показал [13], который рассматривал задачу периодических проверок и многопериодных сроков использования с нулевым временем доставки, избежание сложных вычислений требует создания хорошей аппроксимации для описания точного ожидаемого уровня устаревших запасов. Задача управления запасами скоропортящихся товаров в системе с постоянным контролем при положительном сроке поставки заказа также включает сложные вычисления. Таким образом, [3] представил простую, но достаточно хорошую аппроксимацию ожидаемому уровню устаревших товаров для (Q,r) системы управления запасами скоропортящихся товаров при постоянном контроле с положительным периодом реализации заказа L. Наш приближенный ожидаемый уровень устаревших товаров в текущем объеме заказа Q имеет вид:
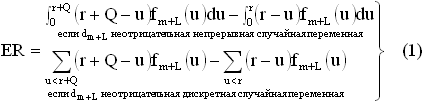
где fm+L(u) – вероятностная функция случайной переменной dm+L (т.е. спроса в течение m+L единиц времени). Уравнение (1) достаточно приемлемой аппроксимацией точного ожидаемого уровня устаревших запасов в ситуации использования стратегии с постоянным контролем. Тут следует отметить, что уравнение (1) аналогично H(x+y) – H(x) представленного в [11] с x, y и m замененными на r, Q и m+L соответственно. Как уравнение (1) может эффективно аппроксимировать точный ожидаемый уровень устаревших запасов более подробно изложено в [3].
4. Случай полного учета неудовлетворенных требований
При полном учете неудовлетворенных требований нет потери продаж, поскольку покупатели или потребители материалов готовы ждать прибытия следующего заказа. Неудовлетворенный спрос затем насыщается прибывшим заказом немедленно. Может использоваться четыре подхода к аппроксимации ожидаемого уровня запасов в единицу времени в (Q,r) системе скоропортящимися запасами:
(1) Крайне грубая аппроксимация
Этот подход полагает, что значения ER и ES намного меньше текущего размера заказа Q. Поэтому, ER и ES можно пренебречь и ожидаемый уровень запасов в единицу времени:
Уравнение (2) предполагает, что нет разницы между тремя случаями дефицита. Однако, уровень запасов не был корректно подсчитан для случая исчерпания запасов (т.е. условие отсутствия на складе).
(2) Аппроксимация Вагнера
В противоположность крайне грубой аппроксимации, Вагнер учитывает оба случая исчерпания и неисчерпания запаса во время доставки заказа. Полагается что ES намного меньше ER и может быть проигнорировано в этой аппроксимации:
где

Функция fL(x) в уравнении (4) – это вероятностная функция случайной переменной dL. В уравнении (3) DL(ES)/(2Q) называется поправочным членом ожидаемого уровня запаса в единицу времени. Понятно, что эта аппроксимация сводится к крайне грубому подходу когда ES игнорируется. Однако, этот подход не принимает во внимание продолжительность отсутствия запаса, т.к. полагает, что когда dL>r, уровень запаса становится нулевым именно перед прибытием пополнения. Цель этой аппроксимации – сделать формулы затрат на содержание несложными.
(3) Модифицированная аппроксимация Вагнера
EIw в уравнении (3) – это переоценка EI вследствие пренебрежения продолжительностью отсутствия запасов и возможностью их устаревания. В этой статье, аппроксимация по [7] без условия старения товаров называется модифицированной аппроксимацией Вагнера. Ссылаясь на выведение среднего перевозимого запаса в [7], ожидаемый уровень запаса в единицу времени в модифицированной модели Вагнера можно выразить как:

Если правую сторону уравнения (5) умножить на h, то результат будет эквивалентен [7] для модели с полным учетом неудовлетворенных требований с b = 1. После дальнейших преобразований (5) можно записать как:

где ES определяется по (4). Заметим, что в уравнениях (5) и (6) знак интеграла может быть заменен на знак суммы, если спрос во время доставки dL – дискретная случайная переменная.
(4) Аппроксимация Chiu
Уравнение (5) выведено при предположении, что ER значительно меньше, чем ES и может быть проигнорировано. Неизбежно, это приводит к неточному значению EI, полученному с использованием модифицированного подхода Вагнера. Пусть
L1 = ожидаемый средний уровень запаса в течение времени доставки;
L2 = ожидаемый средний уровень запаса после прибытия заказа до следующего перезаказа.
Чтобы упростить вывод ожидаемого уровня запасов в единицу времени, предположим что когда dL>r, уровень запасов становиться нулевым точно перед прибытием заказанных единиц. Тогда,
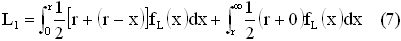
Фактически, уравнение (7) может быть далее приведено к
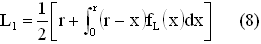
В уравнении (8),
 может быть легко доказан для эквивалентного r – DL + ES. С другой стороны, L2 может быть аппроксимирован точно учитывая четырехугольник, треугольник и параллелограмм, как показано на рисунке 1. Т.о.
может быть легко доказан для эквивалентного r – DL + ES. С другой стороны, L2 может быть аппроксимирован точно учитывая четырехугольник, треугольник и параллелограмм, как показано на рисунке 1. Т.о.где
ER определяется из уравнения (1), и a показывает ожидаемое число циклов пополнения, которые срок использования товара (m) может покрыть; более того, 0<(m–aET)/(ET–L)<1. Другими словами, срок годности в m единиц времени состоит из
![[m/et]](art23.gif) циклов пополнения, где
циклов пополнения, где ![[v]](art24.gif) обозначает наибольшее целое, меньшее или равное v.
Например, на рисунке 1, мы устанавливаем a равным 1.
В дополнение, Tm представляет собой точку окончания срока использования товара, приходящуюся на текущий цикл, которая зависит от реального спроса в течение временного интервала m+L.
обозначает наибольшее целое, меньшее или равное v.
Например, на рисунке 1, мы устанавливаем a равным 1.
В дополнение, Tm представляет собой точку окончания срока использования товара, приходящуюся на текущий цикл, которая зависит от реального спроса в течение временного интервала m+L.Понятно, что уравнение (8) должно быть умножено на DL/(Q – ER) (вследствие того, что L/ET = DL/(Q – ER)). Соответственно, уравнение (9) должно быть умножено на 1–DL/(Q–ER). Умножение двух выражений на два веса соответственно, ожидаемый уровень запаса в единицу времени имеет следующий вид:
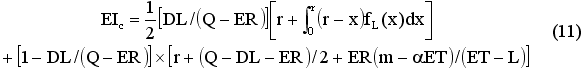
После некоторых преобразований получим:
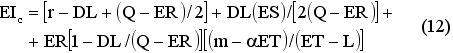
Заметим, что EIc приводится к EIw если ER игнорируется (т.е. ER устанавливается равным нулю). Кроме того, EIc становится EIr когда ER и ES игнорируются. Последние два члена в уравнении (12) – поправочные члены, используемые для увеличения эффективности аппроксимации. Чтобы уменьшить вычислительную сложность, разумно установить Tm равным средней точке временного интервала (ET–L). В результате (m–aET)/(ET–L) становится равным 1/2; т.о.

Из уравнений (2), (3) и (6) заключаем, что
Вообще, мы имеем 0<=ES<=Q. Т.о. (ES–ER)/(Q–ER) <=ES/Q т.к. ER>=0. Уравнения (2), (3) и (13) означают, что
Однако, сложно сравнить EIc c EIm. Мы полагаем, что EIm<=EIс когда значение ER очень мало в уравнении (13). Это можно увидеть, сравнивая непосредственно уравнение (13) с (6). Сейчас, общие ожидаемые средние затраты в единицу времени для случая с полным учетом неудовлетворенных требований имеют вид:
где EI одна из четырех, предложенных выше аппроксимаций. Заметим, что ET, как показано в уравнении (10), также функция от текущего объема заказа Q и точка перезаказа r.
5. Случай с частичным учетом и потерей неудовлетворенных требований
В случае с полной потерей продаж весь неудовлетворенный спрос полностью теряется, и покупатели или пользователи ресурсов возможно удовлетворяют свои потребности из других источников. Однако, в большинстве практических ситуаций, когда предмет на складе отсутствует, некоторые покупатели или потребители ресурсов терпеливо ждут, пока не будет удовлетворен их спрос из следующего заказа первоначального источника, а остальные – нетерпеливы, и делают закупки у других источников для удовлетворения их спроса. В таких обстоятельствах разумно предположить, что только часть дефицита, b (0 <= b <= 1), становится на учет, а остальная часть, 1 – b, теряется навсегда. Вывод ожидаемого уровня запасов в единицу времени для двух случаев дефицита аналогичен случаю, когда весь неудовлетворенный спрос становится на учет. Главная разница между случаями с полным и частичным учетом состоит в том, что в случае с частичным учетом в среднем требуется Q + (1 – b)ES единиц в каждом цикле пополнения, в отличие от Q единиц, которые требуются в случае, когда весь неудовлетворенный спрос становится на учет. Следует заметить, что количество Q (включая b(ES) задолженных единиц) удовлетворяются в то время как (1 – b)ES теряются навсегда. В результате, крайне грубая аппроксимация остается без изменений, а другие три аппроксимации могут легко быть выведены просто заменой Q на Q + (1 – b)ES в соответствующих уравнениях случая с полным учетом неудовлетворенных требований. Результирующие уравнения:

и
где ER определяется по (1), ES – по (4). В одном крайнем случае, когда b=0, случай с частичным учетом неудовлетворенных требований преобразуется в случай с полной потерей продаж, а в другом, когда b=1 – в случай с полным учетом неудовлетворенных требований. Аналогично, случай с частичным учетом и полной потерей имеют те же свойства, которые описаны в выражениях (14) и (15). Общие ожидаемые средние затраты в единицу времени для случая с частичным учетом неудовлетворенных требований имеют вид:
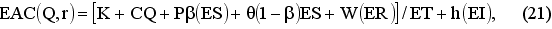
где
6. Численные примеры и анализ чувствительности
В этом разделе будут даны численные примеры и представлены результаты анализа чувствительности. Были использованы и перечислены в таблице 1 24 контрольные задачи, использованные в [3].
Таблица 1. – Параметры стоимости и соответствующие данные 24 тестовых задач
| № тестовой задачи | Затраты | |||
|---|---|---|---|---|
| C | P | K | W | |
| 1 | 5 | 20 | 10 | 5 |
| 2 | 5 | 20 | 50 | 5 |
| 3 | 5 | 20 | 100 | 5 |
| 4 | 5 | 40 | 10 | 5 |
| 5 | 5 | 40 | 50 | 5 |
| 6 | 5 | 40 | 100 | 5 |
| 7 | 15 | 20 | 10 | 5 |
| 8 | 15 | 20 | 50 | 5 |
| 9 | 15 | 20 | 100 | 5 |
| 10 | 15 | 40 | 10 | 5 |
| 11 | 15 | 40 | 50 | 5 |
| 12 | 15 | 40 | 100 | 5 |
| 13 | 5 | 20 | 10 | 15 |
| 14 | 5 | 20 | 50 | 15 |
| 15 | 5 | 20 | 100 | 15 |
| 16 | 5 | 40 | 10 | 15 |
| 17 | 5 | 40 | 50 | 15 |
| 18 | 5 | 40 | 100 | 15 |
| 19 | 15 | 20 | 10 | 15 |
| 20 | 15 | 20 | 50 | 15 |
| 21 | 15 | 20 | 100 | 15 |
| 22 | 15 | 40 | 10 | 15 |
| 23 | 15 | 40 | 50 | 15 |
| 24 | 15 | 40 | 100 | 15 |
L = 1, h = 1, m = 3, q = P, d1 распределена по закону Пуассона с D = 10.
Для иллюстрации цели была выбрана тестовая задача 1 из таблицы 1. Затем, соответствующие уравнения предложенного подхода (включая уравнения (1), (4) и (20)-(21)) были применены для b = 1, 0.5, и 0 соответственно. Мы можем заключить, что ожидаемый уровень запаса в единицу времени возрастает по мере уменьшения доли b.
Таблица 2. – Результаты использования предложенной аппроксимации для задачи 1 при b = 1, 0.5 и 0.
| Решение | b = 1 | b = 0.5 | b = 0 |
|---|---|---|---|
| Q | 13,8417 | 13,9178 | 13,6224 |
| R | 14,5414 | 14,3792 | 14,1564 |
| EIc | 11,4899 | 11,4080 | 11,0981 |
| ER | 0,0571 | 0,0549 | 0,0431 |
| ES | 0,1331 | 0,1471 | 0,1693 |
| ET | 1,3785 | 1,3936 | 1,3749 |
| EAC(Q,r) | 71,08985 | 70,8247 | 70,5319 |
Таблица 3 представляет величины решений EIc, полученных с использованием предложенной аппроксимации и тестовой задачи 1 для различных значений m. Результаты показывают, что для каждой доли b, ожидаемый уровень запасов в единицу времени стремится к фиксированному значению, когда срок годности m возрастает до большого значения (такое значение в этом примере m=5). Чем более длительный срок хранения имеют скоропортящиеся товары, тем менее заметным становиться наличие ограниченного срока хранения. Это означает, что ER->0 по мере роста срока хранения m до достаточно большого значения, и что уравнения (20) затем переходит в уравнение (18). Следовательно (Q, r) модель скоропортящихся запасов сводится к (Q, r)-модели с отсутствием стареющих запасов в случаях с длительным сроком годности.
Таблица 3. – величины решений EIc, полученных с использованием предложенной аппроксимации и тестовой задачи 1 для различных значений m.
| m | b = 1 | b = 0.5 | b = 0 |
|---|---|---|---|
| 2 | 8,7777 | 8,5570 | 8,4990 |
| 3 | 11,4899 | 11,4080 | 11,0981 |
| 4 | 12,5202 | 12,3676 | 12,1288 |
| 5 | 12,5803 | 12,4032 | 12,1890 |
| 6 | 12,5803 | 12,4032 | 12,1890 |
| 7 | 12,5803 | 12,4032 | 12,1890 |
Возникает вопрос, оказывает ли неточная аппроксимация ожидаемого уровня запасов существенное влияние на определение политики заказа (Q, r). Таблица (4) представляет результаты анализа чувствительности с использованием 24 задач таблицы 1.
Таблица 4. – Процентные усреднения для отклонений политики заказов
| Подход к аппроксимации | b = 1 | b = 0.7 | b = 0.4 | b = 0 | ||||
|---|---|---|---|---|---|---|---|---|
| Q | r | Q | r | Q | r | Q | r | |
| Крайне грубый | -0,10% | -0,53% | +0,10% | -0,84% | +0,29% | -0,92% | +0,54% | -1,82% |
| Модифицированный Вагнера | -0,14% | -0,49% | -0,24% | -0,37% | +0,82% | -1,20% | -0,52% | -0,40% |
| Вагнера | -0,03% | -0,52% | -0,35% | -0,18% | -0,16% | -0,03% | -0,07% | -0,19% |
Каждое процентное усреднение в таблице (4) это результат, во-первых, вычитания параметра политики управления запасами (Q или r), который был получен, используя предложенную аппроксимацию из параметра, который был получен, используя одну из трех других аппроксимаций, и затем, деления этого значения на предлагаемый параметр. Положительное процентное усреднение показывает, в какой мере параметр, полученный с использованием аппроксимации был переоценен, в то время как отрицательное значение показывает, что полученный параметр был недооценен. Некоторые важные заключения, возникающие исходя из таблицы 4 следующие:
(1) Для всех значений b, точка перезаказа полученная с использованием всех трех подходов недооценена.
(2) В случае полной потери неудовлетворенных требований (b = 0), отклонения размера заказа Q больше, чем в случае с полностью задолженным спросом. Это можно объяснить тем, что размер заказа Q не включает размер задолженного спроса ES в случае с полной потерей неудовлетворенных требований.
(3) Большинство параметров, полученных с использованием подхода Вагнера, имеют намного более маленькое отклонение, чем параметры, полученные согласно остальным подходам. Предположительно, главная причина этого – то, что величина решения ER очень мала. Т.о., уравнение (18) практически идентично (20). Тем не менее, все параметры, полученные с помощью подхода Вагнера недооценены.
Таблица 5 представляет суммы 24 величин решений EI. Рисунок 2 представляет соотнесенный граф, который показывает относительные значения EI для четырех аппроксимаций и трех случаев дефицита. Отсюда можно заключить, что ожидаемый уровень запасов в единицу времени уменьшается с уменьшением доли b. Также очевидно, что отношения (14) и (15) не противоречат результатам, показанным в таблице 5 или на рисунке 2. Более того, как и ожидалось, значения EI, полученные с использованием модифицированного подхода Вагнера меньше, чем полученные с использованием предложенной аппроксимации, поскольку величины решений ER очень малы в этом анализе.
Таблица 5. – Суммарные величины решений EI
| Подход к аппроксимации | b = 1 | b = 0.7 | b = 0.4 | b = 0 |
|---|---|---|---|---|
| Крайне грубый | 299,4603 | 293,4229 | 283,7080 | 268,7160 |
| Модифицированный Вагнера | 299,5945 | 295,4538 | 290,4995 | 283,3413 |
| Подход Chiu | 301,2300 | 297,8750 | 293,2553 | 286,8325 |
| Вагнера | 302,4031 | 298,7430 | 294,8651 | 287,9539 |
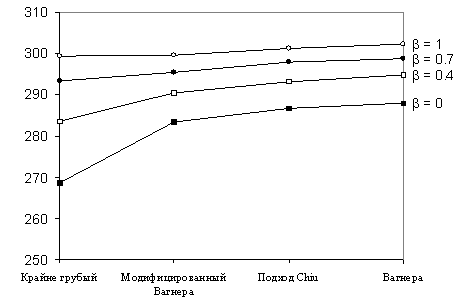
7. Выводы
В этой статье был представлен хороший подход к аппроксимации ожидаемого уровня запасов в единицу времени для (Q, r)-системы скоропортящихся запасов. Были рассмотрены три основных случая реакции покупателей или потребителей материалов на отсутствие запасов. В исследовании было проведено сравнение предложенного подхода с тремя существующими, которые были использованы в ситуациях, когда устаревание или порча запаса не допускается. Очевидно, что предложенная аппроксимация намного проще модифицированного подхода Вагнера. Это можно увидеть, сравнивая уравнения (20) и (19). Она не сложнее по сравнению с аппроксимацией Вагнера. Однако, уравнение (20) – это практическая формула, удобная для использования в (Q, r)-модели управления скоропортящимися запасами, которая может быть сформулирована в форме уравнений (21), (22), (1) и (4). Наилучшая политика заказов (Q, r) может таким образом быть получена корректно, и отклонения в определении Q и r могут быть сведены к минимуму.
В дополнение, результаты, полученные из численных примеров и анализа чувствительности подчеркивают, что величины решений EI недооцениваются при использовании грубого подхода и модифицированного подхода Вагнера. Такой результат часто становится причиной отклонений параметров политики управления запасами. Более существенна значительная недооценка EI вследствие использования крайне грубого подхода, которая приводит к значительным искажениям при определении оптимальной политики заказов. Стоит заметить, что, как показал Браун в [1], важность точной оценки функции затрат на хранение быстро становится очевидной для принимающего решения, чья фирма работает в условиях отрицательного эффекта масштаба (например, порча, распад, износ).
Ссылки:
1. R. M. BROWN, T. E. CONINE and M. TAMARKIN, A Note on Holding Costs and Lot-Size Errors, Decision Sciences, 1986, 17, pp. 603-608.
2. D. CHAZAN and S. GAL, A Markovian Model for a Perishable Product Inventory, Management Science, 1977, 23, pp. 512-521.
3. H. N. CHIU, An Approximation to the Continuous Review Inventory Model with Perishable Items and Lead Times, European Journal of Operational Research, 1995, 87, pp. 93-108.
4. M. A. COHEN, Analysis of Single Critical Number Ordering Policies for Perishable Inventories, Operations Research, 1976, 24, pp. 726-741.
5. C. DAS, (Q, r) Inventory Models with Time-Weighted Backorders, Journal of the Operational Research Society, 1983, 34, pp. 401-412.
6. G. HADLEY and T. M. WHITIN, Analysis of Inventory Systems, Prentice-Hall, Englewood Cliffs, N.J., 1963.
7. D. H. KIN and K. S. PARK, (Q, r) Inventory Model with a Mixture of Lost Sales and Time-Weighted Backorders, Journal of the Operational Research Society, 1985, 36, pp. 231-238.
8. J. LIEBMAN, L. LASDON, L. SCHRAGE and A. WAREN, Modelling and Optimization with GINO, The Scientific Press, Palo Alto, California, 1986.
9. J. P. MATTHEWS, Computation of Constrained Optimum Quantities and Reorder Points for Time-Weighted Backorder Penalties, Naval Research Logistics Quarterly, 1977, 24, pp. 679-690.
10. D. C. MONTGOMERY, M. S. BAZARAA and A. K. KESWANI, Inventory Models with a Mixture of Backorders and Lost Sales, Naval Research Logistics Quarterly, 1973, 20, pp. 255-263.
11. S. NAHMIAS, Myopic Approximations for the Perishable Inventory Problem, Management Science, 1976, 22, pp. 1002-1008.
12. S. NAHMIAS, Higher-Order Approximations for the Perishable-Inventory Problem, Operations Research, 1977, 25, pp. 630-640.
13. S. NAHMIAS, Perishable Inventory Theory: A Review, Operations Research, 1982, 30, pp. 680-708.
14. P. NANDAKUMAR and T. E. MORTON, Near Myopic Heuristics for the Fixed-Life Perishability Problem, Management Science, 1993, 39, pp. 1490-1498.
15. K. S. PARK, Inventory Model with Partial Backorders, International Journal of Systems Science, 1982, 13, pp. 1313-1317.
16. M. J. M. POSNER and B. YANSOUNI, A Class of Inventory Models with Customer Impatience, Naval Research Logistics Quarterly, 1972, 19, pp. 483-492.
17. F. RAAFAT, Survey of Literature on Continuously Deteriorating Inventory Models, Journal of the Operational Research Society, 1991, 42, pp. 27-37.
18. G. RABINOWITZ, A. MEHREZ, C. W. CHU and B. E. PATUWO, A Partial Backorder Control for Continuous Review (r, Q) Inventory System with Poisson Demand and Constant Lead Time, Computers and Operations Research, 1995, 22, pp. 689-700.
19. D. ROSENBERG, A New Analysis of a Lot-Size Model with Partial Backlogging, Naval Research Logistics Quarterly, 1979, 26, pp. 349-353.
20. C. P. SCHMIDT and S. NAHMIAS, (S–1, S) Policies for Perishable Inventory, Management Science, 1985, 31, pp. 719-728.
21. Y. C. SHIUE An Inventory Model for Perishable Items in a Lot-Size System with Quantity Discounts, European Journal of Operational Research, 1990, 45, pp. 260-264.
22. E. A. SILVER, Operations Research in Inventory Management: A Review and Critique, Operations Research, 1981, 29, pp. 628-645.
23. R. J. TERSINE, Principles of Inventory and Materials Management, Prentice-Hall, Englewood Cliffs, N.J., 1994.
24. H. M. WAGNER, Principles of Operations Research with Applications to Managerial Decisions, Prentice-Hall, Englewood Cliffs, N.J., 1975.