Задача совмещения заказов по нескольким номенклатурам.
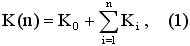
где K0 – цена акта заказа.
Средние суммарные расходы при независимых заказах с оптимальной для каждой номенклатуры периодичностью определяются по формуле (2), а при одновременном заказе всех N номенклатур – по формуле (3).
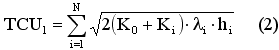
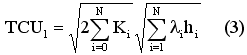
При одновременном заказе всех номенклатур происходит экономия на заказах, но, с другой стороны, при таком подходе периодичность заказа отличается от оптимальной для каждой номенклатуры, что увеличивает расходы. Рыжиков Ю. И. в книге «Теория очередей и управление запасами» предложил систему кратных периодов, соединяющей достоинства обоих подходов. При этом отдельные номенклатуры со сходными значениями стоимостного спроса объединяют в совместно заказываемые группы, что позволяет получить малое расхождение между групповым и индивидуальным оптимумами. Кроме того, за счет кратности периодов снабжения по группам удается достичь частого совмещения заказов.
Пусть
– множество номенклатур с периодичностью поставок kT, k = 1,2,…; nk – число элементов такого множества.
Рыжиков предложил следующий алгоритм планирования многономенклатурных поставок:1) упорядочить номенклатуры по возрастанию отношений {Ki/(lihi)} и произвести их перенумерацию;
2) выбрать начальное приближение для базисного периода Т0. Начальное приближение можно рассчитывать по формуле (4).
3) рассчитать для него оптимальный набор коэффициентов
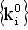.Условием перехода номенклатуры i из множества
в множество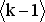 
является неравенство (5).
Момент перехода (правая граница) определяется по формуле (6).
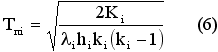
4) рассчитать значения G, H для этих коэффициентов по формулам (7) и (8). Вычислить T* (наиболее выгодный период при постоянной группировке) и L* (минимальные затраты в единицу времени) по формулам (9) и (10) соответственно.
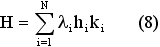
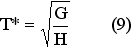
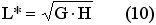
5) по формулам (11) и (6) рассчитать левые и правые границы интервала постоянства группировок.
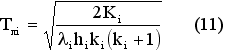
6) установить в нуль указатель key направления изменения T.
7) если существует такое i, что Tпi < T*, положить key = 1; иначе, если существует такое i, что Tлi > T*, положить key = -1 .
8) пока key = -1: установить key = 0. Рассчитать DG (по формуле 12) и DH (по формуле 13) по всем номенклатурам, для которых {Tлi} > T*, найти SDG и SDH; заменить для всех этих номенклатур ki на ki+1 и рассчитать новые {Tлi}. Вычислить новые значения G:= G + DG, H:= H + DH и пересчитать по ним T* и L*. Если корректировки были, установить key = -1 и вернуться на начало пункта.
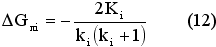
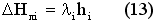
9) пока key = 1: установить key = 0. Рассчитать DG (14) и DH (15) по всем номенклатурам, для которых {Tпi} < T*, найти SDG и SDH; заменить для всех этих номенклатур ki на ki–1 и рассчитать новые {Tпi}. Вычислить новые значения G:= G + DG, H:= H + DH и пересчитать по ним T* и L*. Если корректировки были, установить key = 1 и вернуться на начало пункта.
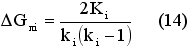
10) восстановить первоначальную нумерацию и выдать T*, L* и набор {ki}.
11) конец алгоритма.