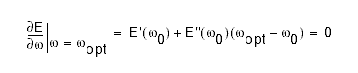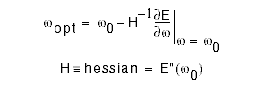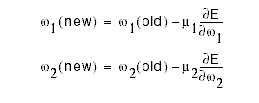Jump to source
Optimal Weight and Learning Rates for Linear Networks
Regression Revisited
Suppose we are given a set of data
(x(1),y(1)),(x(2),y(2))...(x(p),y(p)):
If we assume that g is linear, then finding the best
line that fits the data (linear regression) can be done algebraically:
The solution is based on minimizing the squared error (Cost) between the
network output and the data:
where y = w x.
Finding the best set of weights
1-input, 1 output, 1 weight
But the derivative of E is zero at the
minimum so we can solve for wopt.
n-inputs, m outputs: nm weights
The same analysis can be done in the
multi-dimensional case except that now everything becomes matrices:
where wopt is an mxn matrix, H is an nxn
matrix and ┴ is an mxn matrix.
Matrix inversion is an expensive
operation. Also, if the input dimension, n, is very large then H is huge and may
not even b possible to compute. If we are not able to compute the inverse
Hessian or if we don't want to spend the time, then we can use gradient
descent.
Gradient Descent: Picking the Best Learning
Rate
For linear networks, E is quadratic then
we can write
But this is just a Taylor series
expansion of E(w) about w0. Now, suppose we want to determine the optimal
weight, wopt. We can differentiate E(w) and evaluate the result at wopt, noting
that E`(wopt) is zero:
Solving for wopt we obtain:
comparing this to the update equation,
we find that the learning "rate" that takes us directly to the minimum is equal
to the inverse Hessian, which is a matrix and not a scalar. Why do we need a
matrix?
2-D Example
Curvature axes aligned with the
coordinate axes:
m1
and m2 are inversely related to the size of
the curvature along each axis. Using the above learning rate matrix has the
effect of scaling the gradient differently to make the surface "look"
spherical.
If the axes are not aligned with
coordinate axes, the we need a full matrix of learning rates. This matrix is
just the inverse Hessian. In general, H-1 is not diagonal. We can
obtain the curvature along each axis, however, by computing the
eigenvalues of H. Anyone remember what eigenvalues are??
Taking a Step Back
We have been spending a lot of time on
some pretty tough math. Why? Because training a network can take a long time if
you just blindly apply the basic algorithms. There are techniques that can
improve the rate of convergence by orders of magnitude. However, understanding
these techniques requires a deep understanding of the underlying characteristics
of the problem (i.e. the mathematics). Knowing what speed-up techniques to
apply, can make a difference between having a net that takes 100 iterations to
train vs. 10000 iterations to train (assuming it trains at all).
The previous slides are trying to make
the following point for linear networks (i.e. those networks whose cost function
is a quadratic function of the weights):
- The shape of the cost surface has
a significant effect on how fast a net can learn. Ideally, we want a
spherically symmetric surface.
- The correlation matrix is defined
as the average over all inputs of xxT
- The Hessian is the second
derivative of E with respect to w.
For linear nets, the Hessian is the
same as the correlation matrix.
- The Hessian, tells you about the
shape of the cost surface:
- The eigenvalues of H are a measure
of the steepness of the surface along the curvature directions.
- a large eigenvalue => steep
curvature => need small learning rate
- the learning rate should be
proportional to 1/eigenvalue
- if we are forced to use a single
learning rate for all weights, then we must use a learning rate that will not
cause divergence along the steep directions (large eigenvalue directions).
Thus, we must choose a learning rate m that is on the
order of 1/╗max where ╗max is the largest eigenvalue.
- If we can use a matrix of
learning rates, this matrix is proportional to H-1.
- For real problems (i.e.
nonlinear), you don't know the eigenvalues so you just have to guess. Of
course, there are algorithms that will estimate ╗max ....We won't be
considering these here.
- An alternative solution to
speeding up learning is to transform the inputs (that is, x -> Px, for some
transformation matrix P) so that the resulting correlation matrix,
(Px)(Px)T, is equal to the identity.
- The above suggestions are only
really true for linear networks. However, the cost surface of nonlinear
networks can be modeled as a quadratic in the vicinity of the current weight.
We can then apply the similar techniques as above, however, they will only be
approximations.
[Top]
 [Next:
Summary]
[Next:
Summary]  [Back to the
first page]
[Back to the
first page]


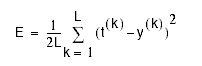

![]()
![]()