А.Б.Сергиенко. Signal Processing Toolbox - обзор
Источник: http://matlab.exponenta.ru/communication/book1/index.php
Обработка сигналов всегда являлась одной из самых главных прикладных областей применения системы MATLAB. Об этом в первую очередь свидетельствует тот факт, что Signal Processing Toolbox был одним из первых специализированных пакетов — он появился уже в 1988 г., всего четыре года спустя после создания самой системы MATLAB.
К настоящему времени пакет Signal Processing содержит почти двести тщательно разработанных специализированных функций, позволяющих решать самые разнообразные задачи анализа и обработки сигналов.
Распространяемая в настоящее время версия MATLAB 6.1 (Release 12.1) содержит пакет Signal Processing версии 5.1. В ожидающуюся в скором времени версию MATLAB 6.5 (Release 13) войдет пакет Signal Processing версии 6.0.
Согласно официальной документации пакета его функции делятся на двадцать категорий. В приведенном ниже списке эти категории объединены в более крупные группы. Итак, по своему назначению функции пакета Signal Processing можно разделить следующим образом:
Кроме того, в состав пакета входят три графических среды:
Далее мы рассмотрим перечисленные категории подробнее.
MATLAB и его пакеты расширения ориентированы прежде всего на цифровую обработку сигналов, поэтому функции, связанные с расчетом аналоговых цепей, рассматриваются как вспомогательные. В основном они предназначены для вызова из других функций, использующих аналоговые прототипы при синтезе цифровых фильтров. Однако и сами по себе эти функции могут быть весьма полезны. В свою очередь, их можно разделить на несколько групп.
Первая группа — функции расчета аналоговых фильтров-прототипов, то есть фильтров нижних частот с частотой среза, равной 1 рад/с. Функции возвращают нули, полюсы и коэффициент усиления фильтров и позволяют рассчитывать фильтры-прототипы Баттерворта (buttap), Чебышева первого рода (cheb1ap), Чебышева второго рода (cheb2ap), эллиптические (Кауэра) (ellipap) и Бесселя (besselap).
Вторая группа — функции преобразования аналоговых фильтров, позволяющие преобразовать ФНЧ-прототип в ФНЧ с другой частотой среза (lp2lp), в фильтр верхних частот (ФВЧ) с заданной частотой среза (lp2hp), в полосовой фильтр с заданными средней частотой и шириной полосы пропускания (lp2bp) и в режекторный фильтр с заданными средней частотой и шириной полосы задерживания (lp2bs). Функции могут принимать и возвращать описания фильтров в виде векторов коэффициентов полиномов числителя и знаменателя функции передачи либо в виде параметров пространства состояний.
Третья группа — функции расчета аналоговых фильтров с заданными параметрами. В процессе расчета они вызывают функции первых двух групп. Набор требуемых для расчета исходных данных включает порядок фильтра, его тип (ФНЧ, ФВЧ, полосовой или режекторный), частоту или несколько частот среза, а также (в зависимости от прототипа) параметры пульсаций амплитудно-частотной характеристики (АЧХ). Имеются функции для расчета фильтров Баттерворта (butter), Чебышева первого рода (cheby1), Чебышева второго рода (cheby2), эллиптических (Кауэра) (ellip) и Бесселя (besself). Все эти функции, кроме функции besself, могут использоваться и для расчета дискретных фильтров (см. далее). Признаком аналогового варианта расчета является указание строки 's' в качестве последнего входного параметра.
Четвертая группа — функции определения требуемого порядка фильтра по заданным параметрам АЧХ (граничным частотам полос пропускания и задерживания, а также допустимым пульсациям в полосах пропускания и задерживания). Для каждого типа фильтра имеется своя функция определения требуемого порядка: для фильтра Баттерворта — buttord, для фильтра Чебышева первого рода — cheb1ord, для фильтра Чебышева второго рода — cheb2ord, для эллиптического фильтра — ellipord. Так же, как и функции предыдущей группы, данные функции позволяют определять требуемый порядок и для дискретных фильтров (см. далее). Признаком аналогового варианта расчета является указание строки 's' в качестве последнего входного параметра.
Пятая группа — функции преобразования форм описания аналоговых линейных систем. Для аналоговых систем поддерживаются четыре таких способа описания:
- Коэффициенты полиномов числителя и знаменателя функции передачи системы.
- Нули, полюсы и коэффициент усиления системы (разложение функции передачи на множители).
- Полюсы и вычеты (представление функции передачи системы в виде суммы простых дробей).
- Параметры пространства состояний.
В пакете Signal Processing имеются функции, реализующие взаимные преобразования этих четырех форм представления аналоговых систем (лишь функция residue, работающая с полюсами и вычетами, относится не к пакету Signal Processing, а к базовой библиотеке MATLAB). Эти функции перечислены в следующей таблице.
Конечная форма |
Коэффициенты полиномов функции передачи |
Нули и полюсы |
Полюсы и вычеты |
Пространство состояний |
Исходная форма |
|
|
|
|
Коэффициенты полиномов функции передачи |
|
tf2zp |
residue |
tf2ss |
Нули и полюсы |
zp2tf |
|
|
zp2ss |
Полюсы и вычеты |
residue |
|
|
|
Пространство состояний |
ss2tf |
ss2zp |
|
|
Как видно из таблицы, одна и та же функция residue может осуществлять преобразование в обоих направлениях. Направление преобразования определяется числом входных и выходных параметров.
Перечисленные в таблице функции, кроме функции residue, могут также осуществлять преобразования дискретных систем, поскольку формулы преобразования для аналоговых и дискретных систем являются одинаковыми.
Наконец, к шестой группе следует отнести единственную функцию freqs, позволяющую рассчитать или отобразить графически амплитудно- и фазочастотную характеристики (АЧХ и ФЧХ) аналоговой линейной системы. Исходными данными являются коэффициенты полиномов числителя и знаменателя функции передачи системы.
В качестве примера применения функций работы с аналоговыми системами рассчитаем эллиптический ФНЧ четвертого порядка с частотой среза 3 кГц, пульсациями АЧХ в полосе пропускания, равными 1 дБ, и с подавлением сигнала в полосе задерживания, равным 20 дБ, а затем построим графики его АЧХ и ФЧХ.
[b, a] = ellip(4, 1, 20, 2*pi*3000, 's'); % расчет фильтра
f = 0:10:10000; % вектор частот для расчета АЧХ и ФЧХ
h = freqs(b, a, 2*pi*f); % комплексный коэффициент передачи
subplot(2, 1, 1)
plot(f, abs(h)) % график АЧХ
grid
subplot(2, 1, 2)
plot(f, unwrap(angle(h))*180/pi) % график ФЧХ (в градусах)
grid
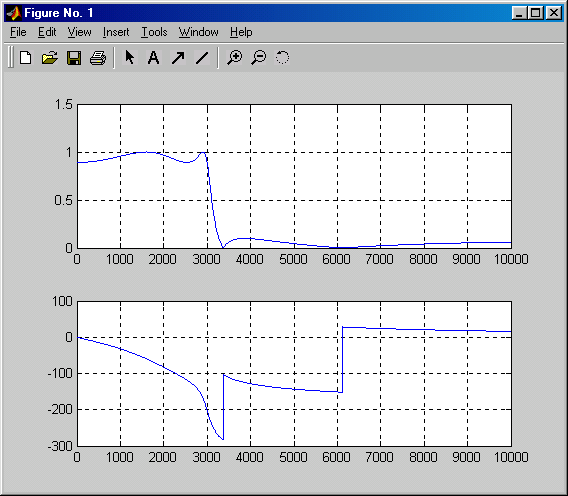
Использованная в коде примера функция unwrap устраняет незначащие скачки ФЧХ на 360°.
Данная категория функций является довольно многочисленной и объединяет разнообразные средства анализа дискретных линейных систем — как правило, представленных в виде векторов коэффициентов полиномов числителя и знаменателя функции передачи (в z-области).
Функция freqz является дискретным аналогом функции freqs, она позволяет рассчитать комплексный коэффициент передачи или построить графики АЧХ и ФЧХ дискретной системы. Исходными данными являются коэффициенты полиномов числителя и знаменателя функции передачи системы.
Аналогично функции freqz работает функция grpdelay, позволяющая рассчитать или графически отобразить частотную зависимость групповой задержки, вносимой дискретным фильтром.
Функция impz предназначена для расчета или графического отображения импульсной характеристики дискретной системы. Исходными данными, как и для предыдущих функций, являются коэффициенты полиномов числителя и знаменателя функции передачи системы.
Функция zplane позволяет отобразить нули и полюсы системы на комплексной плоскости, дополнительно изобразив единичную окружность, ограничивающую допустимую область расположения полюсов устойчивой дискретной системы. Исходными данными могут быть как векторы коэффициентов полиномов числителя и знаменателя, так и непосредственно векторы нулей и полюсов функции передачи системы.
Функция filternorm позволяет рассчитать норму дискретного фильтра. Этот параметр используется, например, при выборе коэффициентов масштабирования отдельных секций фильтра, реализованного в последовательной (каскадной) форме, с целью уменьшения ошибок округления. Поддерживаются два варианта: 2-норма и 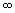 -норма. 2-норма представляет собой среднеквадратическое значение АЧХ фильтра (или, что то же самое, корень из суммы квадратов отсчетов импульсной характеристики фильтра), а -норма. 2-норма представляет собой среднеквадратическое значение АЧХ фильтра (или, что то же самое, корень из суммы квадратов отсчетов импульсной характеристики фильтра), а 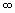 -норма — это максимальное значение АЧХ. -норма — это максимальное значение АЧХ.
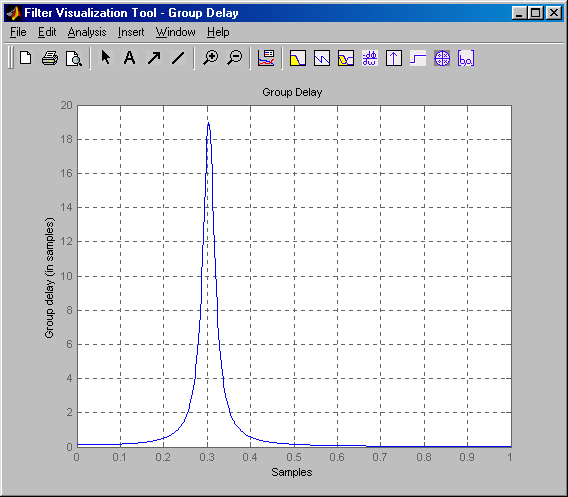
Функция fvtool по существу представляет собой графическую среду, предназначенную для анализа и визуализации характеристик дискретных систем (Filter Visualization Tool). Однако, в отличие от других графических сред пакета, fvtool действительно является функцией, поскольку при вызове требует наличия входных параметров — коэффициентов полиномов числителя и знаменателя функции передачи анализируемого фильтра. Существенным достоинством данной функции является возможность одновременного просмотра характеристик нескольких фильтров. Графический интерфейс пользователя, обеспечиваемый данной функцией, практически такой же, как в среде анализа и синтеза фильтров FDATool. Ниже показаны пример вызова функции fvtool и создаваемое ей графическое окно в режиме показа частотной зависимости вносимой фильтром групповой задержки.
b = [1 2 1];
a = [1 –1.1 0.9];
fvtool(b, a)
Большую группу составляют функции преобразования форм описаний дискретных систем. Для дискретных систем поддерживается больше форм представления, чем для аналоговых:
- Коэффициенты полиномов числителя и знаменателя функции передачи системы.
- Нули, полюсы и коэффициент усиления системы (разложение функции передачи на множители).
- Полюсы и вычеты (представление функции передачи системы в виде суммы простых дробей).
- Параметры пространства состояний.
- Представление в виде набора последовательно (каскадно) включенных секций второго порядка.
- Представление в виде решетчатой или решетчато-лестничной структуры.
Функции, осуществляющие преобразования между различными формами представления, перечислены в следующей таблице.
Конечная форма |
Коэффициенты полиномов функции передачи |
Нули и полюсы |
Полюсы и вычеты |
Пространство состояний |
Секции второго порядка |
Решетчатая структура |
Исходная форма |
|
|
|
|
|
|
Коэффициенты полиномов функции передачи |
|
tf2zp |
residuez |
tf2ss |
tf2sos |
tf2latc |
Нули и полюсы |
zp2tf |
|
|
zp2ss |
zp2sos |
|
Полюсы и вычеты |
residuez |
|
|
|
|
|
Пространство состояний |
ss2tf |
ss2zp |
|
|
ss2sos |
|
Секции второго порядка |
sos2tf |
sos2zp |
|
sos2ss |
|
|
Решетчатая структура |
latc2tf |
|
|
|
|
|
Как видно из таблицы, одна и та же функция residuez (это аналог функции residue, предназначенный для работы с описаниями дискретных систем) может осуществлять преобразование в обоих направлениях. Направление преобразования определяется числом входных и выходных параметров.
Еще две функции осуществляют манипуляции над векторами коэффициентов полиномов, модифицируя положение корней полинома на комплексной плоскости. Функция polyscale умножает все корни обрабатываемого полинома на заданный коэффициент, а функция polystab делает все корни полинома лежащими внутри единичной окружности — для этого корни, превышающие единицу по абсолютной величине, инвертируются, то есть их модули заменяются на обратные величины, а знак их фаз меняется на противоположный.
Оставшиеся функции данной категории являются вспомогательными. Функция freqspace рассчитывает вектор равномерно расположенных значений частот, функция freqzplot предназначена для построения графиков частотных характеристик, а функция unwrap позволяет устранить незначащие скачки фазочастотных характеристик на 2p , отыскивая эти скачки между элементами вектора и сдвигая нужные фрагменты вектора на 2p n.
Функции дискретной фильтрации
Операция линейной дискретной фильтрации в общем случае описывается следующим образом:

Здесь x(k) - отсчеты входного сигнала, y(k) - отсчеты выходного сигнала, ai и bj - постоянные коэффициенты. Максимальное из чисел m и n называется порядком фильтра.
Предыдущие выходные отсчеты могут не использоваться при расчетах, тогда все ai = 0 и фильтр называется нерекурсивным или трансверсальным. Если предыдущие выходные отсчеты используются, фильтр называется рекурсивным.
Линейная дискретная фильтрация относится к технологиям обработки произвольных данных, поэтому соответствующая функция - filter - принадлежит не пакету Signal Processing, а является встроенной в ядро MATLAB. Функция filter2, также принадлежащая базовой библиотеке MATLAB, реализует двумерную дискретную фильтрацию.
Поскольку фильтр с постоянными коэффициентами является линейной стационарной дискретной системой, его реакция на произвольный входной сигнал может быть представлена как дискретная свертка входного сигнала с импульсной характеристикой фильтра:
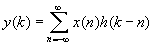
Здесь h(k) - отсчеты импульсной характеристики фильтра. Импульсная характеристика представляет собой реакцию фильтра на поданный на вход одиночный отсчет единичной величины.
Разумеется, вычисления по формуле свертки могут быть реализованы на практике только при конечной длине импульсной характеристики фильтра. Данная операция осуществляется функцией conv; так же как и реализация алгоритма дискретной фильтрации, она относится не к пакету Signal Processing, а к базовой библиотеке MATLAB. В действительности реализация функции conv сводится к вызову функции filter с соответствующими входными параметрами. Функция conv2 реализует двумерную дискретную свертку. Еще одна функция базовой библиотеки MATLAB - deconv - реализует обращение свертки, позволяя по результату свертки и одному из входных векторов определить второй входной вектор.
Упомянутые выше базовые функции дискретной фильтрации, как уже было сказано, относятся к базовой библиотеке MATLAB; собственно же в пакете Signal Processing расположены функции, решающие более специфические задачи фильтрации.
Прежде всего следует отметить, что функция filter дает возможность доступа к начальному и конечному внутренним состояниям фильтра, позволяя за счет этого организовывать блочную обработку сигнала. Иногда при этом возникает необходимость сформировать вектор внутреннего состояния фильтра, зная некоторое количество предыдущих входных и выходных отсчетов. Такой расчет выполняется с помощью функции filtic.
Функция fftfilt реализует дискретную фильтрацию с использованием быстрого преобразования Фурье (БПФ) в сочетании с разделением сигнала на блоки. Таким способом могут быть реализованы только нерекурсивные фильтры. Результат работы функции совпадает (с точностью до вычислительных погрешностей) с результатами обычной фильтрации, реализуемой с помощью функции filter. Однако скорость вычислений при фильтрации с помощью БПФ может оказаться существенно выше, особенно если длина входного сигнала во много раз превышает длину импульсной характеристики фильтра (или наоборот).
Функция filtfilt позволяет компенсировать фазовый сдвиг, вносимый при обычной фильтрации (иными словами, данная функция реализует фильтрацию без внесения временной задержки). Осуществляется это путем двунаправленной обработки сигнала. Первый проход фильтрации осуществляется обычным образом, а затем полученный выходной сигнал фильтруется второй раз - от конца к началу. За счет этого происходит компенсация фазовых сдвигов, а результирующий порядок фильтра увеличивается в два раза. Следует отметить, что для результирующего (эквивалентного двум проходам фильтрации) фильтра не выполняется условие причинности.
При практической реализации рекурсивных фильтров высокого порядка они часто представляются в виде последовательно включенных секций второго порядка. Это позволяет ослабить погрешности вычислений, возникающие из-за ошибок округления и квантования коэффициентов фильтра. Средства анализа ошибок такого рода сосредоточены в пакете Filter Design, а в пакете Signal Processing имеется функция sosfilt, позволяющая реализовать дискретную фильтрацию данных с помощью фильтра, представленного в виде секций второго порядка.
Еще одной возможной структурой дискретного фильтра является решетчатая структура. Для осуществления фильтрации с помощью фильтра, представленного в такой форме, предназначена функция latcfilt.
Функция medfilt1, реализующая одномерную медианную фильтрацию, относится к нелинейным алгоритмам фильтрации. Сущность ее работы состоит в том, что к входному сигналу применяется скользящее окно заданной длины, отсчеты в пределах окна упорядочиваются и в качестве выходного отсчета возвращается значение из середины упорядоченного окна (или полусумма двух ближайших к середине элементов, если окно имеет четную длину). Медианная фильтрация применяется, например, для устранения импульсных помех (щелчков) при обработке звуковых сигналов. Функция medfilt2, реализующая двумерный вариант медианной фильтрации, расположена в пакете Image Processing.
Функция sgolayfilt осуществляет дискретную фильтрацию с помощью фильтра Савицкого-Голея. Сущность ее заключается в том, что входной сигнал разбивается на блоки заданного размера и в пределах каждого блока выполняется полиномиальная аппроксимация сигнала полиномом заданной степени по критерию минимума среднеквадратической ошибки. Если степень полиномов на единицу меньше размера блоков, выходной сигнал будет равен входному; при меньшей степени полиномов будет происходить сглаживание сигнала. Фильтры Савицкого-Голея применяются для "очистки" сигналов от шумов.
Функции синтеза дискретных фильтров
Под синтезом дискретного фильтра понимается выбор таких наборов коэффициентов {ai} и {bi}, при которых характеристики получающегося фильтра удовлетворяют заданным требованиям. Строго говоря, в задачу проектирования входит и выбор подходящей структуры фильтра с учетом конечной точности вычислений. Это особенно актуально при реализации фильтров "в железе" - с использованием специализированных БИС или цифровых сигнальных процессоров. Эффекты, связанные с конечной точностью вычислений, можно анализировать с помощью функций пакета Filter Design; функциями синтеза фильтров эти эффекты не учитываются.
В пакете Signal Processing имеется большое количество функций, реализующих разнообразные алгоритмы синтеза дискретных фильтров. Приведем основные характеристики этих функций в виде таблицы, а затем дадим некоторые дополнительные комментарии.
Функция |
Тип фильтра |
АЧХ |
Метод синтеза |
butter |
Рекурсивный |
Баттерворта |
Билинейное z-преобразование |
cheby1 |
Рекурсивный |
Чебышева первого рода |
Билинейное z-преобразование |
cheby2 |
Рекурсивный |
Чебышева второго рода |
Билинейное z-преобразование |
ellip |
Рекурсивный |
Кауэра (эллиптическая) |
Билинейное z-преобразование |
bilinear |
Рекурсивный |
Произвольный аналоговый прототип |
Билинейное z-преобразование |
impinvar |
Рекурсивный |
Произвольный аналоговый прототип |
Инвариантное преобразование импульсной характеристики |
yulewalk |
Рекурсивный |
Кусочно-линейная |
Авторегрессионный метод |
invfreqz |
Рекурсивный |
Произвольная |
Минимизация разности между числителем функции передачи и произведением ее знаменателя и желаемой ЧХ |
prony |
Рекурсивный |
Синтез по заданной импульсной характеристике |
Экспоненциальная аппроксимация Прони |
fir1 |
Нерекурсивный |
Многополосная |
Обратное преобразование Фурье с использованием окон |
fir2 |
Нерекурсивный |
Кусочно-линейная |
Обратное преобразование Фурье с использованием окон |
firls |
Нерекурсивный |
Кусочно-линейная с переходными полосами |
Минимизация среднеквадратической ошибки |
fircls |
Нерекурсивный |
Кусочно-постоянная |
Минимизация среднеквадратической ошибки с ограничением максимального отклонения |
fircls1 |
Нерекурсивный |
ФНЧ, ФВЧ |
Минимизация среднеквадратической ошибки с ограничением максимального отклонения |
firrcos |
Нерекурсивный |
ФНЧ |
Косинусоидальное сглаживание |
intfilt |
Нерекурсивный |
ФНЧ |
Минимаксная аппроксимация |
remez |
Нерекурсивный |
Кусочно-линейная с переходными полосами |
Минимаксная аппроксимация |
cremez |
Нерекурсивный (в том числе с нелинейной ФЧХ и комплексными коэффициентами) |
Кусочно-линейная с переходными полосами |
Минимаксная аппроксимация |
Методы синтеза дискретных фильтров можно разделить на две большие группы: с использованием и без использования аналогового прототипа. При использовании аналогового фильтра-прототипа необходимо каким-либо образом представлять аналоговую функцию передачи, заданную в s-области, в дискретную функцию передачи, заданную в z-области. В пакете Signal Processing реализованы два метода такого преобразования: метод инвариантной импульсной характеристики и метод билинейного z-преобразования. Оба метода в результате дают рекурсивные дискретные фильтры.
При использовании метода инвариантной импульсной характеристики происходит дискретизация импульсной характеристики аналогового прототипа. Частотная характеристика получающегося дискретного фильтра, соответственно, представляет собой периодически повторенную частотную характеристику аналогового прототипа. По этой причине данный метод непригоден для синтеза фильтров верхних частот и вообще фильтров, коэффициент передачи которых не стремится к нулю с ростом частоты. Метод инвариантной импульсной характеристики реализован в пакете Signal Processing с помощью функции impinvar.
При использовании метода билинейного z-преобразования происходит искажение характеристики аналогового прототипа только вдоль частотной оси. При этом частотный диапазон аналогового фильтра (от нуля до бесконечности) преобразуется к рабочему диапазону частот дискретного фильтра (от нуля до половины частоты дискретизации). Преобразование частотной оси описывается функцией арктангенса, поэтому частоты, значительно меньшие частоты дискретизации, преобразуются приблизительно линейно. Данный метод реализуется с помощью функции bilinear для произвольного аналогового прототипа. Кроме того, имеются готовые функции расчета фильтров нижних и верхних частот, полосовых и режекторных фильтров методом билинейного z-преобразования по аналоговым прототипам с АЧХ Баттерворта, Чебышева первого и второго рода, а также Кауэра (эллиптические фильтры). Это соответственно функции butter, cheby1, cheby2 и ellip. Все эти функции могут использоваться и для расчета аналоговых фильтров (см. ранее). Признаком дискретного варианта расчета является отсутствие строки 's' в списке входных параметров. Имеются также функции определения требуемого порядка этих фильтров по заданным параметрам АЧХ (граничным частотам полос пропускания и задерживания, а также допустимым пульсациям в этих полосах). Это соответственно функции buttord, cheb1ord, cheb2ord, ellipord. Так же, как и функции синтеза фильтров, данные функции позволяют определять требуемый порядок и для аналоговых фильтров (см. ранее). Признаком дискретного варианта расчета является отсутствие строки 's' в списке входных параметров.
В качестве примера синтезируем эллиптический ФНЧ четвертого порядка с такими же параметрами, как у аналогового фильтра в одном из предыдущих примерах (частота среза 3 кГц, пульсации АЧХ в полосе пропускания 1 дБ, и подавление сигнала в полосе задерживания 20 дБ). Частоту дискретизации примем равной 12 кГц. После синтеза построим графики АЧХ и ФЧХ полученного фильтра с помощью функции freqz.
Fs = 12000; % частота дискретизации
F0 = 3000; % частота среза
[b, a] = ellip(4, 1, 20, F0/Fs*2); % расчет фильтра
freqz(b, a, [], Fs); % вывод графиков
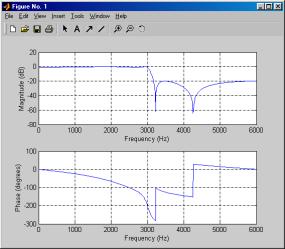
Методы синтеза, не использующие аналоговый прототип, называются прямыми. Их, в свою очередь, можно также разделить на две группы: методы синтеза рекурсивных и нерекурсивных фильтров.
К функциям прямого синтеза нерекурсивных фильтров относятся следующие:
- Функции, реализующие синтез фильтров путем обратного преобразования Фурье от желаемой АЧХ с последующим умножением получившейся импульсной характеристики на некоторую весовую функцию (окно) для ослабления пульсаций АЧХ, появляющихся из-за эффекта Гиббса. Это функции fir1 и fir2. Сюда же можно отнести функцию синтеза ФНЧ с косинусоидальным сглаживанием АЧХ - firrcos. Кроме того, функция kaiserord позволяет по заданным параметрам АЧХ оценить требуемый порядок фильтра при синтезе с использованием окна Кайзера.
- Функции, реализующие минимизацию среднеквадратического отклонения АЧХ получающегося фильтра от заданной. Это функции firls, fircls и fircls1. Последние две функции решают оптимизационную задачу с ограничением максимального отклонения АЧХ от заданной. Это позволяет избежать появления больших выбросов АЧХ вблизи переходных полос.
- Функции, реализующие минимаксную оптимизацию, то есть минимизацию пикового отклонения АЧХ получающегося фильтра от заданной. В результате получаются фильтры с равномерными пульсациями АЧХ. К данной группе относятся функции remez (стандартный вариант метода Ремеза, реализованный еще в самых первых версиях пакета Signal Processing) и cremez (расширенный вариант, поддерживающий синтез фильтров с нелинейной ФЧХ и с комплексными коэффициентами). Кроме того, функция remezord позволяет по заданным параметрам АЧХ оценить требуемый порядок фильтра при синтезе методом Ремеза.
В качестве примера синтезируем методом Ремеза нерекурсивный ФНЧ 32-го порядка с теми же частотами среза и дискретизации, как в предыдущем примере (частота среза 3 кГц, частота дискретизации 12 кГц). Начало полосы задерживания зададим равным 3,5 кГц. После синтеза построим графики импульсной характеристики, а также АЧХ полученного фильтра (ФЧХ фильтра линейна, поэтому выводить ее график не имеет смысла). АЧХ выведем в линейном масштабе по вертикали, чтобы наглядно продемонстрировать равномерность ее пульсаций.
Fs = 12000; % частота дискретизации
F0 = 3000; % частота среза
F1 = 3500; % начало полосы задерживаниЯ
b = remez(32, [0 F0/Fs*2 F1/Fs*2 1], [1 1 0 0]); % расчет фильтра
impz(b) % график импульсной характеристики
[h, f] = freqz(b, 1, [], Fs); % комплексный коэффициент передачи
figure
plot(f, abs(h)) % график АЧХ
grid
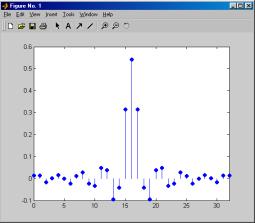 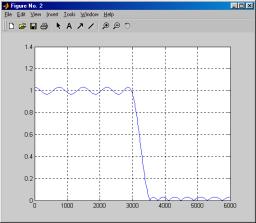
К функциям прямого синтеза рекурсивных фильтров относятся следующие:
- yulewalk - синтез рекурсивного фильтра с произвольной кусочно-линейной АЧХ методом Юла-Уолкера.
- invfreqz - данная функция предназначена для решения задачи идентификации систем, она позволяет определить коэффициенты числителя и знаменателя функции передачи дискретной системы по набору значений этой функции передачи на различных частотах.
В завершение перечислим еще ряд функций, не вошедших в перечисленные выше группы. Функция maxflat предназначена для синтеза обобщенного фильтра Баттерворта (у таких фильтров число нулей функции передачи превышает число ее полюсов). Функция intfilt выполняет синтез фильтров, предназначенных для фильтрации сигнала при выполнении интерполяции и прореживания. Операцию свертки векторов можно представить как векторно-матричное произведение, а матрицу, участвующую в этом произведении, рассчитать с помощью функции convmtx. Наконец, функция sgolay выполняет синтез сглаживающего фильтра Савицкого-Голея. Поскольку, как описывалось выше, фильтр Савицкого-Голея обрабатывает отдельные блоки сигнала, такой фильтр не является стационарной системой. Поэтому функция sgolay возвращает целую матрицу меняющихся во времени коэффициентов эквивалентного нерекурсивного фильтра.
Кроме пакета Signal Processing, ряд функций синтеза дискретных фильтров имеется в пакетах Communications и Filter Design.
Функции спектрального анализа и статистической обработки сигналов
Слова "спектральный анализ" в сознании многих пользователей MATLAB прочно ассоциируются с функцией fft (см. далее раздел "Функции преобразований дискретных сигналов"), выполняющей дискретное преобразование Фурье (ДПФ). Однако это всего лишь взаимно-однозначное линейное преобразование, дающее представление детерминированного сигнала в частотной области. Если же анализируемый сигнал является случайным, для него имеет смысл только оценка спектральной плотности мощности, для расчета которой приходится тем или иным способом выполнять усреднение имеющихся данных. Кроме того, в ряде случаев нам известна некоторая дополнительная информация об анализируемом сигнале, и эту информацию желательно учесть при спектральном анализе.
Методы спектрального анализа случайных сигналов делятся на два больших класса — непараметрические и параметрические. В непараметрических (nonparametric) методах используется только информация, содержащаяся в отсчетах анализируемого сигнала. Параметрические (parametric) методы предполагают наличие некоторой статистической модели случайного сигнала, а процесс спектрального анализа в данном случае включает в себя определение параметров этой модели. Используется также термин "модельный спектральный анализ" (Model-Based Spectrum Analysis, MBSA).
В пакете Signal Processing имеются функции, реализующие разнообразные методы спектрального анализа — как параметрические, так и непараметрические (необходимо еще раз подчеркнуть, что под спектральным анализом здесь имеется в виду оценка спектральной плотности мощности случайного процесса). Кроме того, имеются функции для получения других усредненных характеристик случайных дискретных сигналов.
Спектр дискретного случайного процесса
Для определения спектральных характеристик дискретного случайного процесса вычисляется средний спектр мощности его ограниченного по длине фрагмента, а затем длина фрагмента устремляется к бесконечности:
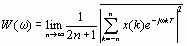 . (1) . (1)
Здесь x(k) — отсчеты случайного процесса, T — период дискретизации. Черта сверху обозначает усреднение по ансамблю реализаций.
Кроме того, этот спектр можно выразить через корреляционную функцию случайного процесса:
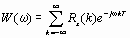 . (2) . (2)
Это выражение представляет собой дискретный аналог теоремы Винера—Хинчина: спектр дискретного случайного процесса является преобразованием Фурье от его корреляционной функции.
Непараметрические методы
Как уже говорилось, при использовании непараметрических методов расчета спектра случайного процесса используется только информация, заключенная в отсчетах сигнала, без каких-либо дополнительных предположений. В пакете Signal Processing реализованы три таких метода — периодограмма, метод Уэлча (Welch) и метод Томсона (Thomson).
Периодограммой (periodogram) называется оценка спектральной плотности мощности, полученная по N отсчетам одной реализации случайного процесса согласно определению (1) (естественно, не путем взятия предела, а усреднением конечного числа слагаемых). Если при расчете спектра используется весовая функция (окно), полученная оценка спектра мощности называется модифицированной периодограммой (modified periodogram):
Соотношение (2) выполняется только при бесконечном числе используемых отсчетов, поэтому при любом конечном N периодограммная оценка спектральной плотности мощности оказывается смещенной — получается, что внутри суммы (2) корреляционная функция сигнала умножается на треугольную весовую функцию. Кроме того, можно показать, что периодограмма не является состоятельной оценкой спектральной плотности мощности, поскольку дисперсия такой оценки сравнима с квадратом ее математического ожидания при любом N. С ростом числа используемых отсчетов значения периодограммы начинают все быстрее флуктуировать — ее график становится все более изрезанным.
В пакете Signal Processing вычисление периодограммы (в том числе модифицированной) производится с помощью функции periodogram.
Для уменьшения изрезанности периодограммы необходимо применить какое-либо усреднение. Бартлетт (Bartlett) предложил разделять анализируемый сигнал на неперекрывающиеся сегменты, вычислять для каждого сегмента периодограмму и затем эти периодограммы усреднять. Если корреляционная функция сигнала на длительности сегмента затухает до пренебрежимо малых значений, то периодограммы отдельных сегментов можно считать независимыми. Уэлч (Welch) внес в метод Бартлетта два усовершенствования: использование весовой функции и разбиение сигнала на перекрывающиеся фрагменты. Применение весовой функции позволяет ослабить растекание спектра и уменьшить смещение получаемой оценки спектра плотности мощности ценой незначительного ухудшения разрешающей способности. Перекрытие сегментов введено для того, чтобы увеличить их число и уменьшить дисперсию оценки.
Вычисления при использовании метода Уэлча (он называется еще методом усреднения модифицированных периодограмм — averaged modified periodogram method) организуются следующим образом: вектор отсчетов сигнала делится на перекрывающиеся сегменты, каждый сегмент умножается на используемую весовую функцию, для взвешенных сегментов вычисляются модифицированные периодограммы, периодограммы всех сегментов усредняются.
Метод Уэлча является наиболее популярным периодограммным методом спектрального анализа. В пакете Signal Processing он реализуется с помощью функции pwelch.
Метод Томсона, реализуемый функцией pmtm, основан на использовании вытянутых сфероидальных функций (prolate spheroidal functions). Эти функции конечной длительности обеспечивают максимальную концентрацию энергии в заданной полосе частот. Помимо собственно спектральной оценки, функция pmtm может возвращать ее доверительный интервал. Для вычисления вытянутых сфероидальных функций требуется некоторое время, поэтому при многократном использовании функции pmtm можно ускорить расчеты, заранее рассчитав необходимые для анализа функции и сохранив их в базе данных. Для работы с такой базой (она представляет собой MAT-файл с именем dpss.mat) предназначено семейство функций, имена которых начинаются с букв dpss (dpss — расчет функций, dpssload — загрузка семейства функций из базы данных, dpsssave — сохранение семейства функций в базе данных, dpssdir — вывод каталога базы данных, dpssclear — удаление семейства функций из базы данных).
В качестве примера сформируем реализацию экспоненциально-коррелированного случайного процесса и произведем ее спектральный анализ тремя перечисленными методами. Необходимый нам случайный сигнал формируется путем пропускания нормального дискретного белого шума через рекурсивный фильтр первого порядка:
X0 = randn(1, 1000);
a = 0.9;
X = filter(1, [1 -a], X0);
Строим периодограмму:
periodogram(X, [], [], 1)
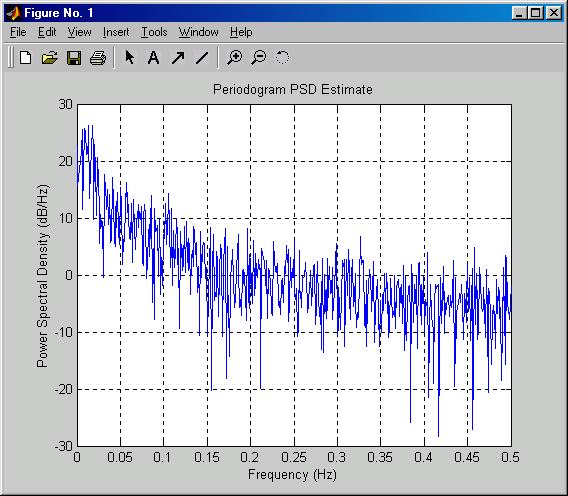
Как видите, периодограмма оказывается весьма изрезанной. Теперь выполним оценку спектра той же реализации методом Уэлча:
pwelch(X, [], [], [], 1)
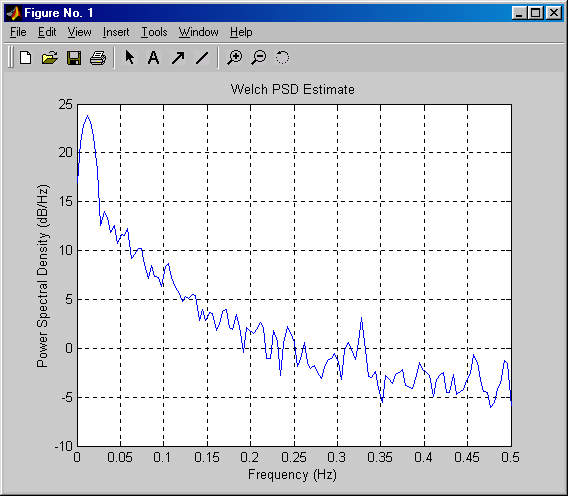
Изрезанность графика оказывается значительно меньшей. Наконец, используем метод Томсона:
pmtm(X, [], [], 1)
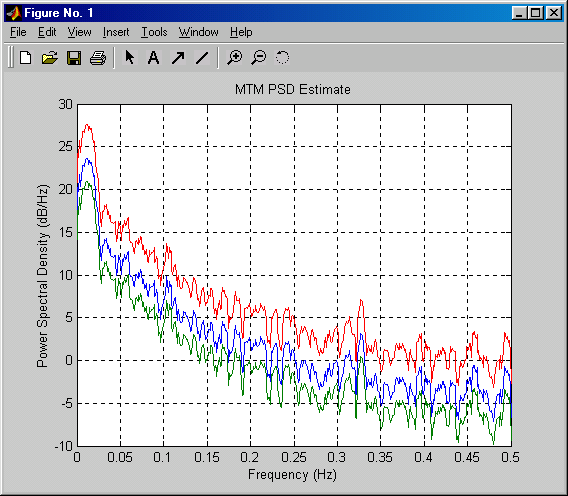
На выводимом функцией pmtm графике вместе с оценкой спектра мощности показаны границы доверительного интервала.
Параметрические методы
Использование параметрических методов подразумевает наличие некоторой математической модели анализируемого случайного процесса. Спектральный анализ сводится в данном случае к решению оптимизационной задачи, то есть поиску таких параметров модели, при которых она наиболее близка к реально наблюдаемому сигналу. В пакете Signal Processing реализован ряд разновидностей авторегрессионного анализа и два метода, основанных на анализе собственных чисел и векторов корреляционной матрицы сигнала: MUSIC (MUltiple SIgnal Classification) и EV (EigenVectors).
Авторегрессионные методы
Согласно авторегрессионной модели сигнал формируется путем пропускания дискретного белого шума через "чисто рекурсивный" фильтр N-го порядка. Спектральная плотность мощности такого сигнала пропорциональна квадрату модуля коэффициента функции передачи формирующего фильтра. Таким образом, данный метод спектрального анализа сводится к определению коэффициентов фильтра заданного порядка, оценке мощности возбуждающего белого шума и аналитическому расчету спектральной плотности мощности. Для определения коэффициентов модели производится минимизация ошибки линейного предсказания сигнала. Теоретический анализ показывает, что оптимальные коэффициенты модели определяются лишь корреляционной функцией сигнала.
На практике мы не знаем истинной корреляционной функции исследуемого сигнала, поэтому для минимизации ошибки предсказания используются оценки КФ, полученные путем временного усреднения. Был разработан целый ряд методов авторегрессионного анализа, отличающихся в основном подходом к обработке краевых эффектов (то есть к способу вовлечения в вычисления тех краевых отсчетов сигнала, для которых при вычислении КФ не оказывается сдвинутой пары). В пакете Signal Processing реализованы метод Берга (Burg), ковариационный метод, модифицированный ковариационный метод и авторегрессионный метод Юла—Уолкера (Yule—Walker).
Авторегрессионные методы анализа спектра больше всего подходят для сигналов, действительно являющихся авторегрессионными процессами. Вообще, хорошие результаты эти методы дают тогда, когда спектр анализируемого сигнала имеет четко выраженные пики. В частности, к таким сигналам относится сумма нескольких синусоид с шумом.
При использовании авторегрессионных методов важно правильно выбрать порядок авторегрессионной модели — он должен быть в два раза больше числа синусоидальных колебаний, которые предположительно содержатся в анализируемом сигнале.
Каждому методу авторегрессионного анализа в пакете Signal Processing соответствуют две функции — функция вычисления коэффициентов модели и функция собственно спектрального анализа. Функция спектрального анализа вызывает функцию расчета коэффициентов модели, а затем производит вычисление спектра. Имена функций сведены в следующую таблицу.
Название метода |
Функция расчета коэффициентов модели |
Функция спектрального анализа |
Ковариационный метод |
arcov |
pcov |
Модифицированный ковариационный метод |
armcov |
pmcov |
Метод Берга |
arburg |
pburg |
Авторегрессионный метод Юла—Уолкера |
aryule |
pyulear |
Сформированный в приведенном выше примере экспоненциально-коррелированный случайный сигнал является авторегрессионным процессом первого порядка, поэтому перечисленные методы спектрального анализа являются для него вполне адекватными. Применим метод Берга, задав порядок авторегрессионной модели, равный единице (это второй параметр функции pburg):
pburg(X, 1, [], 1)
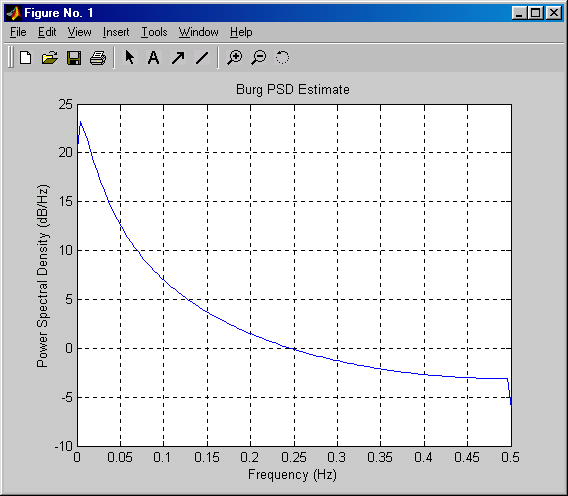
Полученная гладкая кривая практически совпадает с теоретическим спектром данного случайного процесса.
Методы, основанные на анализе собственных чисел и векторов корреляционной матрицы
Метод MUSIC (MUltiple SIgnal Classification) предназначен для спектрального анализа сигналов, представляющих собой сумму нескольких синусоид (точнее, в общем случае — нескольких комплексных экспонент) с белым шумом. Целью спектрального анализа подобных сигналов, как правило, является не расчет спектра как такового, а определение частот и уровней (амплитуд или мощностей) гармонических составляющих. Метод MUSIC предназначен именно для этого, поэтому получаемая с его помощью зависимость уровня сигнала от частоты называется псевдоспектром (pseudospectrum).
В основе метода лежит анализ собственных чисел и собственных векторов корреляционной матрицы сигнала. При выполнении анализа необходимо указать порядок модели, то есть число комплексных экспонент, предположительно содержащихся в сигнале.
В пакете Signal Processing метод MUSIC реализован с помощью функции pmusic, а функция rootmusic позволяет получить оценки частот и мощностей гармонических составляющих сигнала.
Близким родственником MUSIC является метод анализа собственных векторов (eigenvectors, EV). Его отличие состоит лишь в том, что в расчетных формулах собственные векторы умножаются на весовые коэффициенты, обратно пропорциональные соответствующим собственным числам. В литературе приводятся сведения о том, что метод EV порождает меньше ложных спектральных пиков, чем MUSIC, и, как правило, лучше передает форму спектра шума.
В пакете Signal Processing метод EV реализован с помощью функции peig, а функция rooteig позволяет получить оценки частот и мощностей гармонических составляющих сигнала.
Следует подчеркнуть, что псевдоспектры не являются оценками истинного спектра плотности мощности, а представляют собой лишь спектральные псевдооценки, позволяющие оценивать частоты синусоидальных или узкополосных составляющих сигнала с разрешением, несколько превосходящим разрешение авторегрессионных методов.
Весовые функции (окна)
Дискретное преобразование Фурье, используемое во всех непараметрических методах спектрального оценивания, подразумевает периодическое продолжение анализируемого фрагмента сигнала. При этом на стыках фрагментов могут возникать скачки, приводящие к появлению боковых лепестков значительного уровня в спектральной области. Для ослабления этого эффекта сигнал перед выполнением ДПФ умножают на спадающую от центра к краям весовую функцию (окно). В результате величина скачков на стыках сегментов уменьшается, меньше становится и уровень нежелательных боковых лепестков спектра — платой за это является некоторое расширение спектральных пиков.
Помимо спектрального анализа весовые функции применяются при синтезе нерекурсивных фильтров путем обратного преобразования Фурье желаемой частотной характеристики. В этом случае они позволяют увеличить подавление сигнала в полосе задерживания фильтра за счет некоторого расширения полосы пропускания.
В настоящее время пакет Signal Processing содержит примерно полтора десятка весовых функций. Распространение некоторых из них обусловлено вычислительной простотой, другие же являются в каком-либо смысле оптимальными.
Простейшим является прямоугольное окно, реализуемое функцией rectwin (в версиях пакета до 5.0 включительно данная функция имела имя boxcar). Прямоугольное окно соответствует отсутствию взвешивания, данная функция включена в состав пакета лишь для формальной полноты набора весовых функций. Треугольное окно реализуется функцией triang, треугольную форму имеет и окно Бартлетта (функция bartlett), оно лишь несколько отличается способом расчета.
Несколько весовых функций являются комбинациями гармонических составляющих. Перечислим их в порядке возрастания числа косинусоидальных слагаемых:
- Окно Ханна (функция hann), иногда неправильно называемое окном Хэннинга — одно косинусоидальное слагаемое.
- Окно Хэмминга (функция hamming) — одно косинусоидальное слагаемое.
- Окно Блэкмена (функция blackman) — два косинусоидальных слагаемых.
- Окно Блэкмена—Харриса (функция blackmanharris) — три косинусоидальных слагаемых.
- Окно Наттолла (альтернативная версия окна Блэкмена—Харриса, функция nuttallwin) — три косинусоидальных слагаемых.
Остальные окна описываются более сложными математическими соотношениями. Форма гауссова окна (функция gausswin) не требует пояснений. Модифицированное окно Бартлетта—Ханна (функция barthannwin) представляет собой линейную комбинацию окон Бартлетта и Ханна. Окно Бомена (функция bohmanwin) является сверткой двух одинаковых косинусоидальных импульсов. Окно Чебышева (функция chebwin) обладает боковыми лепестками фиксированного (задаваемого при расчете) уровня и рассчитывается путем обратного преобразования Фурье частотной характеристики окна. Окно Кайзера (функция kaiser) также обладает параметром, регулирующим уровень боковых лепестков и ширину главного лепестка, при расчете данного окна используются модифицированные функции Бесселя. Окно Тьюки (функция tukeywin) является прямоугольником с косинусоидально сглаженными краями. При крайних допустимых значениях коэффициента сглаживания оно превращается в прямоугольное окно или окно Ханна.
Наконец, функция window предоставляет общий интерфейс для вызова функций расчета конкретных окон.
Другие функции статистического анализа
Функции, относящиеся к данной категории, вычисляют различные статистические параметры сигналов. Функции можно разделить на несколько групп.
Первая группа относится к вычислению корреляционных и ковариационных функций (здесь следует напомнить, что в отечественной и зарубежной терминологии эти понятия не совпадают; в данном обзоре используется зарубежный вариант, принятый в MATLAB). Функция xcorr позволяет оценить корреляционную функцию сигнала или взаимную корреляционную функцию двух сигналов. Вариант этой функции, предназначенный для работы с двумерными сигналами, имеет имя xcorr2. Функция xcov предназначена для оценивания ковариационной функции сигнала или взаимной ковариационной функции двух сигналов. Функции cov и corrcoef, входящие в базовую библиотеку MATLAB, позволяют получить соответственно ковариационную матрицу и матрицу коэффициентов корреляции путем усреднения нескольких реализаций случайных данных. Функция corrmtx возвращает матрицу промежуточных данных для оценки корреляционной матрицы сигнала, а также может возвращать и саму эту матрицу.
Следующая группа функций производит расчет статистических характеристик в частотной области, используя непараметрический метод Уэлча (см. выше). Функция csd предназначена для оценивания взаимной спектральной плотности двух случайных процессов. Она также может возвращать доверительный интервал для полученной оценки. Функция cohere дает оценку квадрата модуля функции взаимной когерентности двух случайных процессов. Функция tfe позволяет оценить комплексный коэффициент передачи системы по реализациям ее входного и выходного сигналов.
Наконец, функция psdplot используется всеми функциями спектрального оценивания для вывода графика спектральной плотности мощности. Ее можно вызывать и в явном виде — например, чтобы вывести график в линейном масштабе вместо принятого по умолчанию логарифмического или чтобы показать несколько спектров на одном графике.
Функции параметрического моделирования и линейного предсказания
Параметрическое моделирование
Под параметрическим моделированием понимаются выбор некоторой математической модели случайного процесса и последующий подбор параметров этой модели для обеспечения максимального соответствия между сигналом, формируемым моделью, и имеющейся в наличии реальной выборкой данных.
Одной из широко используемых на практике является авторегрессионная (AR) модель, в которой случайный сигнал формируется путем пропускания дискретного белого шума через “чисто рекурсивный” (то есть не использующий задержанных отсчетов входного сигнала) формирующий фильтр. Четыре функции пакета Signal Processing — arburg, arcov, armcov и aryule — предназначены для получения оценок коэффициентов формирующего фильтра и дисперсии (мощности) возбуждающего фильтр белого шума. Методы расчета, используемые этими функциями, были указаны ранее, в разделе “Авторегрессионные методы”, где шла речь об авторегрессионном спектральном анализе.
Если в нашем распоряжении имеется оценка комплексного коэффициента передачи системы на различных частотах, можно построить реализуемую модель системы, частотная характеристика которой будет максимально близкой к измеренной. Под реализуемостью системы здесь подразумевается представимость ее функции передачи в виде дробно-рациональной функции с заданными порядками полиномов числителя и знаменателя. Параметрическое моделирование в данном случае сводится к нахождению оптимальных коэффициентов полиномов числителя и знаменателя функции передачи. Данная задача решается двумя функциями пакета Signal Processing: функция invfreqs позволяет построить модель аналоговой системы, а функция invfreqz выполняет аналогичную операцию применительно к дискретным системам.
Еще один вариант задачи параметрического моделирования предполагает построение модели системы по имеющейся оценке ее импульсной характеристики. Для этого в пакете Signal Processing имеются две функции. Функция prony использует тот факт, что импульсная характеристика рекурсивной дискретной системы при отсутствии у нее кратных полюсов представляет собой сумму дискретных экспоненциальных функций (в общем случае комплексных). Алгоритм, реализуемый данной функцией, был первоначально разработан в 18 веке бароном де Прони с целью подгонки параметров экспоненциальной аналитической модели под экспериментальные данные. Устойчивость полученной системы не гарантируется, однако первые n отсчетов (n — заданный при расчете порядок числителя функции передачи системы) ее импульсной характеристики точно совпадают с заданными.
Вторая функция моделирования системы по импульсной характеристике — функция stmcb — не стремится обеспечить точное совпадение начальных фрагментов импульсных характеристик — вместо этого она минимизирует квадратичное отклонение полученной характеристики от заданной, то есть сумму квадратов модулей разностей отсчетов полученной и желаемой импульсных характеристик. Функция реализует итерационный метод Штейглица—МакБрайда, который сводится к многократному решению системы линейных уравнений относительно коэффициентов полиномов функции передачи искомой системы.
В качестве примера получим методами Прони и Штейглица—МакБрайда модель системы третьего порядка, задав в качестве образца треугольную импульсную характеристику:
h = [1 2 3 4 5 4 3 2 1]; % импульснаЯ характеристика
[b1, a1] = prony(h, 3, 3); % метод Прони
[b2, a2] = stmcb(h, 3, 3); % метод Штейглица—МакБрайда
% графики импульсных характеристик полученных систем
impz(b1, a1, 30)
title('Prony')
figure
impz(b2, a2, 30)
title('Stmcb')
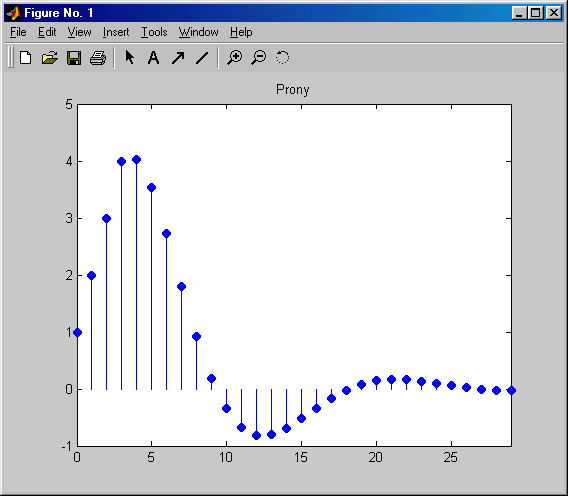
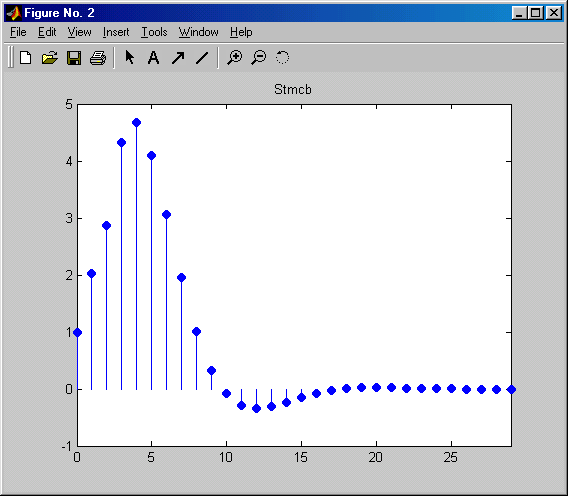
Сравнение графиков наглядно демонстрирует различия двух алгоритмов. При использовании метода Прони первые четыре отсчета полученной импульсной характеристики точно совпадают с заданными, однако в дальнейшем отклонения от заданных величин сильно возрастают, а после окончания заданного фрагмента наблюдается “хвост” с довольно большим уровнем, так как функция prony не делает никаких предположений о требуемых значениях импульсной характеристики за пределами заданного фрагмента. Функция stmcb минимизирует квадратичную ошибку воспроизведения заданной бесконечной импульсной характеристики, при этом по окончании явно заданного фрагмента она считается равной нулю. В результате точного соответствия отсчетов заданной и полученной импульсных характеристик не наблюдается (за исключением первого), зато ошибка воспроизведения характеристики “размазана” по отсчетам более равномерно.
Линейное предсказание
Если дискретный случайный процесс не является белым шумом, его отсчеты оказываются коррелированными друг с другом. Это позволяет, зная корреляционную функцию процесса, предсказывать значение его очередного отсчета. Предсказанное значение вычисляется как линейная комбинация предыдущих отсчетов процесса. В этом состоит основная идея линейного предсказания. Линейное предсказание используется для параметрического спектрального анализа (см. ранее), идентификации систем, анализа речевых сигналов и сжатия информации при их передаче.
Модели систем, основанные на линейном предсказании, могут быть представлены в различных формах и, соответственно, описаны с помощью различных наборов параметров. Ряд функций пакета Signal Processing позволяет преобразовывать описание модели из одной формы в другую. Эти функции перечислены в следующей таблице.
Конечная форма |
Автокорре- ляционная последовательность |
Коэффициенты отражения |
Коэффициенты предсказания |
Арксинусные параметры |
Логарифми- ческие отношения |
Частоты спектральных линий |
Исходная форма |
|
|
|
|
|
|
Автокорреляционная последовательность |
|
ac2rc, schurrc |
ac2poly |
|
|
|
Коэффициенты отражения |
rc2ac |
|
rc2poly |
rc2is |
rc2lar |
|
Коэффициенты предсказания |
poly2ac |
poly2rc |
|
|
|
poly2lsf |
Арксинусные параметры |
|
is2rc |
|
|
|
|
Логарифмические отношения |
|
lar2rc |
|
|
|
|
Частоты спектральных линий |
|
|
lsf2poly |
|
|
|
Кроме того, в пакете Signal Processing имеется еще несколько функций, связанных с линейным предсказанием. Так, для расчета коэффициентов предсказывающего фильтра необходимо решить систему линейных уравнений, матрица которой представляет собой корреляционную матрицу входного сигнала. Эта матрица обладает рядом свойств, благодаря которым можно сократить число вычислительных операций, требующихся для решения системы линейных уравнений. Во-первых, корреляционная матрица является самосопряженной (то есть не меняется после применения к ней эрмитова сопряжения — сочетания транспонирования с комплексным сопряжением). Для вещественного сигнала самосопряженность означает просто симметрию матрицы относительно главной диагонали. Во-вторых, в случае стационарного случайного процесса (а только для таких процессов можно использовать предсказывающий фильтр с постоянными параметрами) корреляционная матрица является матрицей Теплица — вдоль ее диагоналей, параллельных главной, стоят одинаковые числа. Наконец, правая часть системы уравнений представляет собой сдвинутый на одну позицию первый столбец корреляционной матрицы. Системы линейных уравнений с матрицами, обладающими указанными свойствами, называются системами уравнений Юла—Уолкера, а для их решения был разработан рекурсивный метод Левинсона—Дурбина. Данный итерационный алгоритм реализуется функцией levinson. Функция rlevinson решает обратную задачу — позволяет найти вектор отсчетов корреляционной функции сигнала по заданным коэффициентам линейного предсказания.
Функция lpc реализует расчет коэффициентов линейного предсказания автокорреляционным методом и является аналогом функции aryule (см. ранее раздел, посвященный параметрическому спектральному анализу). Эти две функции различаются лишь MATLAB-кодом, используемым для вычисления оценки корреляционной матрицы. Даваемые ими результаты совпадают с точностью до вычислительных погрешностей.
Функции генерации сигналов
В пакете Signal Processing имеется целый ряд функций, предназначенных для генерации сигналов стандартной формы, часто встречающихся при решении различных задач обработки сигнала.
Генерация непериодических сигналов
Все функции генерации непериодических сигналов получают в качестве параметров вектор моментов времени и дополнительные аргументы, описывающие параметры формируемого импульса. Возвращаемым результатом является вектор отсчетов результирующего сигнала. Имеются функции для генерации сигналов следующей формы:
- rectpuls — генерация одиночного прямоугольного импульса, единственным дополнительным параметром является длительность импульса;
- tripuls — генерация одиночного треугольного импульса, дополнительными параметрами являются длительность импульса и коэффициент его асимметрии;
- sinc — генерация импульса, имеющего прямоугольный спектр, по формуле sinc(x) = sin(p x)/(p x). Дополнительных параметров данная функция не имеет;
- gauspuls — генерация радиоимпульса с гауссовой огибающей. Дополнительными параметрами являются несущая частота, относительная ширина спектра и уровень (в децибелах), по которому эта ширина спектра измеряется;
- gmonopuls — генерация гауссова моноимпульса (его форма является первой производной от гауссовой функции). Дополнительным параметром является средняя частота спектра формируемого сигнала.
Генерация периодических сигналов
Функции, относящиеся к данной группе, получают в качестве параметров вектор моментов времени и дополнительные аргументы, описывающие параметры формируемого импульса. Период формируемых сигналов равен 2p . Для формирования сигналов с иным периодом необходимо соответствующим образом масштабировать передаваемый функции временной аргумент. Возвращаемым результатом является вектор отсчетов результирующего сигнала. Имеются функции для генерации периодических сигналов следующей формы:
- square — генерация периодической последовательности прямоугольных импульсов. Дополнительным параметром является коэффициент заполнения импульсов (отношение длительности импульса к периоду их следования);
- sawtooth — генерация периодического пилообразного сигнала. Дополнительным параметром является коэффициент асимметрии треугольных импульсов, составляющих периодическую последовательность;
- diric — функция Дирихле. Дополнительным параметром является целочисленный порядок функции. Функция Дирихле рассчитывается по формуле diric(x) = sin(nx/2)/(n sin(x/2));
Генерация колебаний с изменяющейся частотой
К данной группе относятся две функции — chirp и vco. Функция chirp генерирует колебания, мгновенная частота которых изменяется по одному из трех возможных законов — линейному, квадратичному или экспоненциальному. Более широкими возможностями обладает функция vco (Voltage Controlled Oscillator — генератор, управляемый напряжением), которая позволяет формировать колебания с произвольным законом изменения мгновенной частоты. По сути дела данная функция осуществляет частотную модуляцию.
Генерация последовательности импульсов
Функция pulstran служит для генерации конечной последовательности импульсов одинаковой формы с произвольно задаваемыми задержками и амплитудными множителями. Форма импульсов может задаваться одним из двух способов: именем функции, генерирующей импульс, либо уже рассчитанным вектором отсчетов.
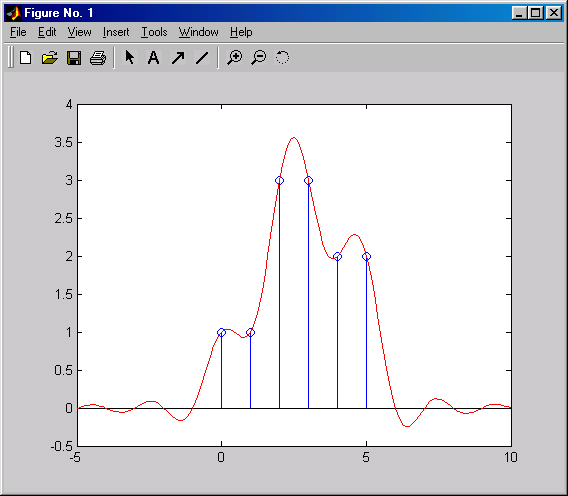
В качестве примера рассмотрим применение функций pulstran и sinc для восстановления аналогового сигнала по его дискретным отсчетам согласно теореме Котельникова.
t = -5:0.1:10; % время для аналогового сигнала
k = 0:5; % номера отсчетов дискретного сигнала
sd = [1 1 3 3 2 2]; % дискретный сигнал
sa = pulstran(t, [k' sd'], 'sinc'); % восстановленный аналоговый сигнал
stem(k, sd) % график дискретного сигнала
hold on
plot(t, sa, 'r') % график аналогового сигнала
hold off
Функции преобразований дискретных сигналов
Пожалуй, наиболее известным из преобразований дискретных сигналов является дискретное преобразование Фурье (ДПФ). Соответствующая функция, использующая алгоритм быстрого преобразования Фурье (БПФ), в MATLAB относится к категории функций обработки данных и является встроенной (функции fft и ifft — одномерный вариант, fft2 и ifft2 — двумерный вариант, fftshift и ifftshift — перестановка половин вектора спектральных отсчетов для переноса нулевой частоты в середину вектора). Собственно же в пакете Signal Processing содержатся функции, реализующие более специфические преобразования.
Как и любое линейное преобразование, ДПФ может быть представлено как умножение матрицы преобразования на столбец отсчетов преобразуемого сигнала. Эта матрица преобразования для ДПФ вычисляется функцией dftmtx.
Опять-таки благодаря линейности ДПФ любой спектральный отсчет может быть представлен как результат обработки исходного сигнала некоторым фильтром. Представление этого фильтра в рекурсивной форме дает алгоритм Герцеля, реализуемый функцией goertzel. Если необходимо вычислить лишь некоторые спектральные отсчеты, данный алгоритм оказывается быстрее, чем БПФ.
Близким родственником ДПФ является дискретное косинусное преобразование. При его вычислении вместо периодического продолжения сигнала, что предполагается при ДПФ, соседние фрагменты продолженного сигнала зеркально переворачиваются во времени. В результате сигнал становится четной функцией времени, а его спектр — вещественным. По этой причине в формуле ДПФ вместо комплексных экспонент фигурируют лишь косинусы, что и дало название данному преобразованию. Прямое и обратное дискретные косинусные преобразования вычисляются функциями dct и idct соответственно.
Важным методом анализа дискретных числовых последовательностей является z-преобразование, результатом которого является функция комплексной переменной z:
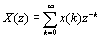 . .
В ряде задач необходимо вычислять z-преобразование для точек 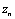 , расположенных на спиральном контуре: , расположенных на спиральном контуре: 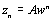 . Эффективный в вычислительном отношении расчет z-преобразования вдоль такого контура использует быстрое преобразование Фурье; он реализован в функции czt. . Эффективный в вычислительном отношении расчет z-преобразования вдоль такого контура использует быстрое преобразование Фурье; он реализован в функции czt.
При реализации некоторых вариантов алгоритма быстрого преобразования Фурье для повышения эффективности необходимо переставить элементы обрабатываемого вектора в обратном битовом порядке (это означает, что в двоичных представлениях номеров элементов вектора биты считываются в обратном порядке, а затем вектор упорядочивается в соответствии с новыми номерами элементов). Для выполнения такой перестановки служит функция bitrevorder.
При анализе узкополосных сигналов бывает полезно представить сигнал в виде колебания с меняющимися во времени амплитудой и начальной фазой. Для получения такого представления используется комплексный аналитический сигнал, вещественная часть которого совпадает с исходным сигналом, а мнимая определяется преобразованием Гильберта от исходного сигнала. В частотной области аналитический сигнал характеризуется односторонним спектром: его спектральная функция отлична от нуля только для положительных частот. Функция hilbert осуществляет расчет аналитического сигнала в частотной области, вычисляя прямое ДПФ, обнуляя половину спектра и затем вычисляя обратное ДПФ.
В качестве примера вычислим аналитический сигнал для прямоугольного радиоимпульса:
s = zeros(256,1);
s(65:192) = cos(pi/2*(0:127)'); % отсчеты радиоимпульса
sa = hilbert(s); % аналитический сигнал
f = (-128:127)/128; % значения нормированных частот для графиков
subplot(2,1,1)
plot(f, abs(fftshift(fft(s)))) % спектр вещественного сигнала
subplot(2,1,2)
plot(f, abs(fftshift(fft(sa)))) % спектр аналитического сигнала
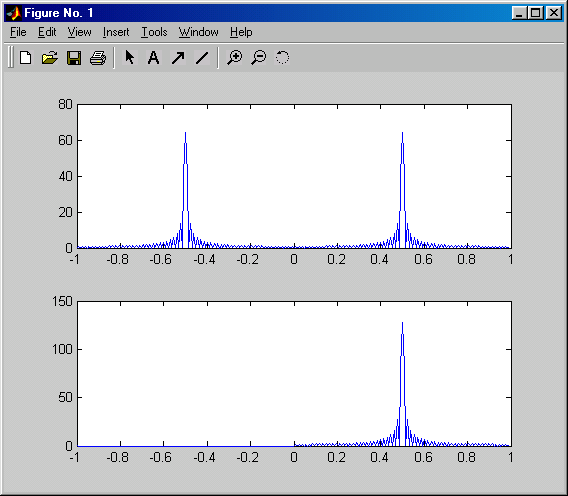
На нижнем графике хорошо видно обнуление спектра в области отрицательных частот и его удвоение в области положительных частот.
Кепстральный анализ
Кепстральный анализ связан с гомоморфной обработкой сигналов. Такая обработка подчиняется обобщенному принципу суперпозиции: если входной сигнал системы представляет собой комбинацию из нескольких сигналов, полученную с помощью математической операции А, то на выходе результаты обработки отдельных сигналов комбинируются с помощью операции Б. Кепстральный анализ нашел свое применение, в частности, в задачах обработки речи. В пакете Signal Processing имеется несколько функций, связанных с кепстральным анализом.
Функция rceps рассчитывает вещественный кепстр сигнала, при этом игнорируется информация, содержащаяся в фазовом спектре. Эта же функция позволяет получить минимально-фазовую реконструкцию сигнала. Нули z-преобразования последовательности отсчетов такого сигнала лежат на комплексной плоскости внутри единичной окружности, а его кепстр совпадает с кепстром исходного сигнала.
Комплексный кепстр, вычисляемый с помощью функции cceps, учитывает как амплитудную, так и фазовую информацию, поэтому его связь с исходным сигналом является взаимно-однозначной. Обратное преобразование, то есть вычисление сигнала по известному комплексному кепстру, выполняется функцией icceps.
Изменение частоты дискретизации
К преобразованиям можно отнести и группу функций, осуществляющих изменение частоты дискретизации сигнала. Наиболее часто частоту дискретизации необходимо изменять в целое число раз. В случае увеличения частоты дискретизации данная операция называется интерполяцией, а в случае уменьшения — прореживанием (decimation). Любой пересчет частоты дискретизации требует последовательного выполнения нескольких действий. В пакете Signal Processing имеются функции, реализующие как отдельные действия, так и необходимые их последовательности.
Для выполнения интерполяции между отсчетами сигнала вставляется требуемое количество нулей (функция upsample), затем полученный сигнал пропускается через фильтр нижних частот. Вместе эти два этапа реализуются функцией interp.
Для выполнения прореживания сигнал пропускается через фильтр нижних частот, а затем из него выбирается каждый N-й отсчет (функция downsample). Вместе эти два этапа реализуются функцией decimate.
Комбинация операций интерполяции и прореживания позволяет изменять частоту дискретизации с коэффициентом, выражающимся произвольной рациональной дробью. Для повышения эффективности вычислений такой пересчет выполняется специализированной функцией resample, а она, в свою очередь вызывает функцию upfirdn (вставка нулей, фильтрация и прореживание). Основное различие между этими двумя функциями состоит в том, что upfirdn позволяет задавать импульсную характеристику используемого фильтра, а при использовании функции resample фильтр рассчитывается автоматически.
Наконец, для абсолютно произвольного пересчета отсчетных моментов могут использоваться общие функции интерполяции, содержащиеся в базовой библиотеке MATLAB, такие как interp1 и spline.
В качестве примера выполним интерполяцию сигнала, использованного выше для демонстрации функций pulstran и sinc, повысив частоту дискретизации в четыре раза. По краям сигнала добавлены нулевые отсчеты, поскольку функция interp требует, чтобы длина исходной последовательности была не менее девяти отсчетов.
sd = [0 0 1 1 3 3 2 2 0 0]; % исходный сигнал
t = 0:9; % дискретное время для исходного сигнала
sd4 = interp(sd, 4); % интерполяция
t4 = (0:39)/4; % дискретное время для интерполированного сигнала
stem(t, sd) % график исходного сигнала
hold on
plot(t4, sd4, 'x') % график интерполированного сигнала
hold off
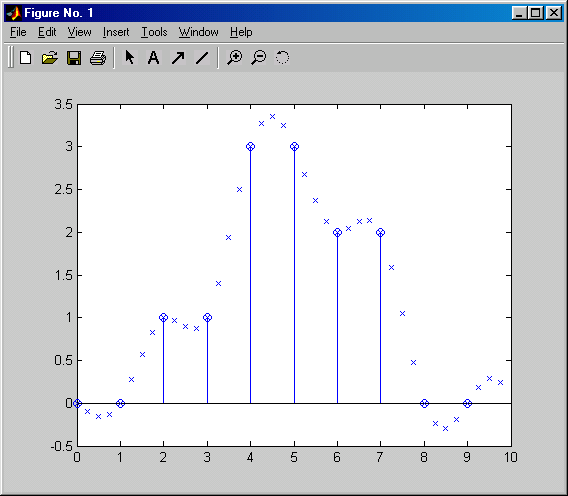
На приведенном графике исходный сигнал показан “стебельками”, а интерполированный — крестиками.
Вспомогательные функции
Данная группа содержит довольно большое число функций. Многие из них предназначены в первую очередь “для внутреннего использования” — они вызываются другими функциями пакета. Однако ряд функций этой категории имеет вполне самостоятельную ценность.
Функция buffer позволяет представлять вектор отсчетов сигнала в матрицу последовательных кадров, причем эти кадры могут перекрываться.
Функции mod и demod осуществляют соответственно модуляцию и демодуляцию. Поддерживаются следующие виды модуляции: амплитудная, амплитудная с подавленной несущей, однополосная, фазовая, частотная, квадратурная, широтно-импульсная, время-импульсная.
Функции uencode и udecode реализуют соответственно равномерное квантование и восстановление сигнала по номерам уровней квантования.
Функция strips предназначена для вывода графика сигнала в несколько строк. Это бывает полезно, если необходимо охватить взглядом длинный сигнал целиком, а разрешение по вертикальной оси не имеет большого значения.
Семейство функций, имена которых начинаются с символов dpss, предназначено для расчета дискретных вытянутых сфероидальных функций и работы с базой данных, предназначенной для хранения рассчитанных функций. Дискретные вытянутые сфероидальные функции используются при спектральном анализе методом Томсона (см. выше раздел “Функции спектрального анализа и статистической обработки сигналов”, подраздел “Непараметрические методы”).
Функции cell2sos и sos2cell позволяют хранить информацию о фильтре, представленном в виде последовательно включенных секций второго порядка, не только в виде матрицы, но и в виде массива ячеек. Эти две функции осуществляют преобразование представления между указанными двумя формами.
Функция specgram осуществляет расчет спектрограммы сигнала, то есть спектров последовательных фрагментов сигнала, выделяемых с помощью скользящего окна. Результаты вычислений могут возвращаться в виде матрицы либо отображаться цветом в координатах “время—частота”.
Функция cplxpair выделяет комплексно-сопряженные пары в векторах комплексных чисел.
Функция eqtflength позволяет выровнять длины двух векторов путем дополнения более короткого из них нулями в конце.
Функция seqperiod предназначена для проверки элементов вектора на периодичность и определение периода их повторения.
Программа синтеза и анализа фильтров — FDATool (Filter Design & Analysis Tool)
Программа синтеза и анализа фильтров FDATool (Filter Design & Analysis Tool) является оболочкой для вызова функций синтеза и анализа дискретных фильтров. При наличии пакета Filter Design Toolbox данная программа также позволяет анализировать эффекты, связанные с квантованием коэффициентов фильтров, и производить преобразования типов фильтров (ФНЧ в ФВЧ и т. п.).
Программа позволяет не только рассчитывать фильтры “с нуля”, но также сохранять и загружать сеансы работы, редактировать ранее сохраненные фильтры. Кроме того, можно импортировать описание фильтра из рабочей области MATLAB или из файлов формата XILINX CORE Generator (*.coe). Импортированные фильтры можно только анализировать.
При анализе можно просматривать следующие характеристики фильтров (в последних версиях пакета можно просматривать несколько графиков одновременно):
- Амплитудно-частотную характеристику (АЧХ).
- Фазочастотную характеристику (ФЧХ).
- АЧХ и ФЧХ одновременно.
- Групповую задержку.
- Фазовую задержку.
- Импульсную характеристику.
- Переходную характеристику.
- Расположение нулей и полюсов на комплексной плоскости.
- Коэффициенты фильтра.
- Информацию о структуре фильтра.
Рассчитанный фильтр можно использовать следующим образом:
- Сохранить сеанс работы для последующей загрузки в программу FDATool с целью дальнейшего редактирования и анализа.
- Экспортировать в рабочую область MATLAB.
- Экспортировать в текстовый файл.
- Экспортировать в MAT-файл.
- Экспортировать в заголовочный (*.h) файл языка C.
- Экспортировать в программу SPTool (см. далее).
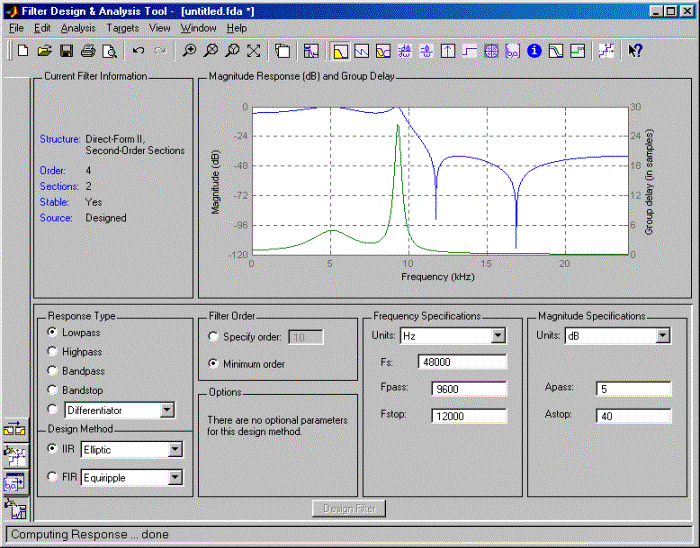
На приведенном ниже рисунке показан вид окна программы FDATool с результатами расчета эллиптического фильтра нижних частот методом билинейного z-преобразования. Отображаются графики АЧХ и групповой задержки.
Программа обработки сигналов — SPTool (Signal Processing Tool)
Программа обработки сигналов SPTool (Signal Processing Tool) позволяет выполнять следующие операции: импортировать сигналы из MAT-файлов или рабочей области MATLAB; просматривать графики сигналов (в том числе нескольких одновременно); применять к сигналам различные методы спектрального анализа и просматривать полученные графики; рассчитывать дискретные фильтры с использованием функций пакета (в том числе путем прямого редактирования расположения нулей и полюсов); пропускать сигналы через фильтры и анализировать получающиеся выходные сигналы.
Следует отметить, что в части анализа и синтеза фильтров возможности программы SPTool являются более узкими, чем у программы FDATool (единственным исключением является отсутствующая в FDATool возможность прямого редактирования расположения нулей и полюсов). Впрочем, эти ограничения компенсируются возможностью экспорта рассчитанного фильтра из FDATool в SPTool.
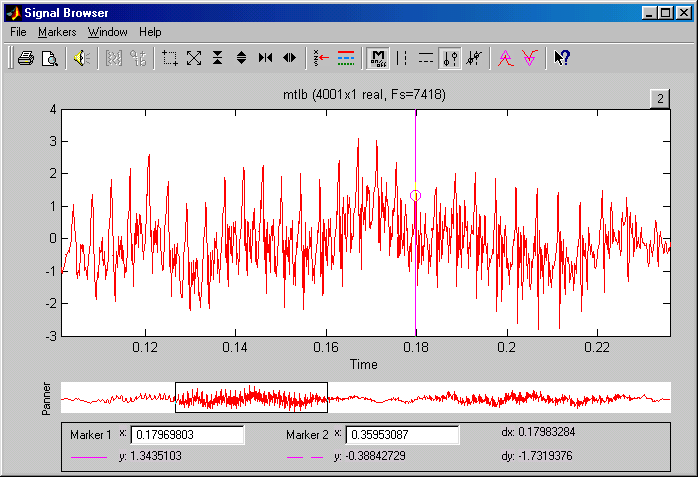
На приведенных ниже рисунках показан вид окна программы SPTool при просмотре графика сигнала, при анализе спектра и при редактировании расположения нулей и полюсов фильтра.
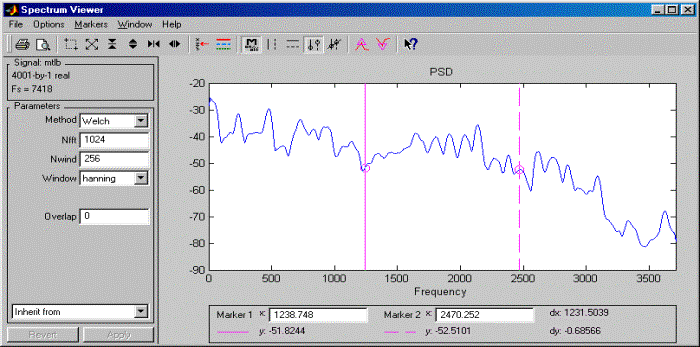
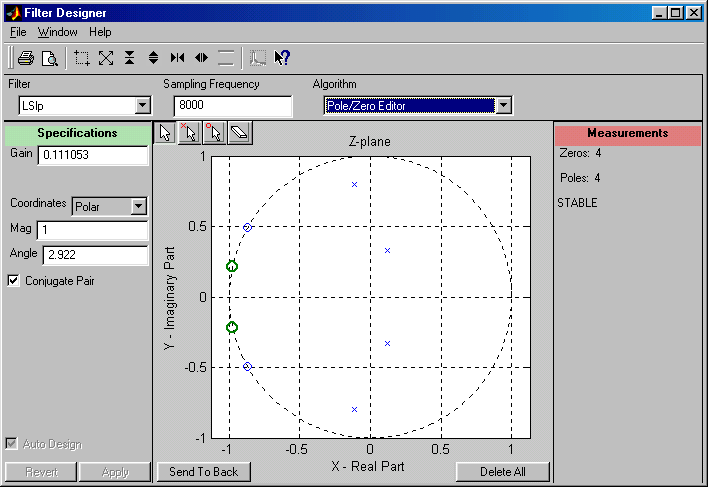
Программа синтеза и анализа весовых (оконных) функций WinTool (Window Design and Analysis Tool)
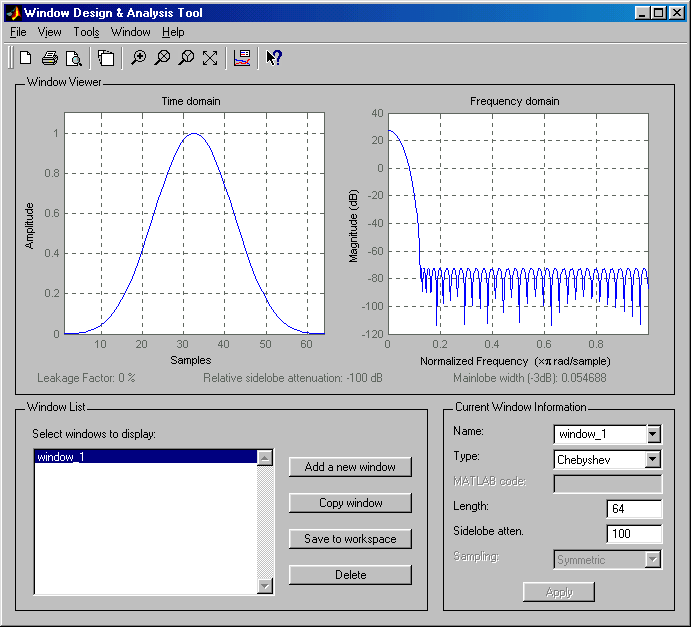
Появившаяся в версии пакета 6.0 (R13) программа синтеза и анализа весовых (оконных) функций WinTool (Window Design and Analysis Tool) является оболочкой для вызова имеющихся в пакете функций расчета окон. При этом демонстрируются характеристики окна (или нескольких окон одновременно) во временной и частотной областях.
На приведенном ниже рисунке показан вид окна программы WinTool с результатами расчета окна Чебышева 64-го порядка с уровнем боковых лепестков спектра –100 дБ. Отображаются график окна во временной области и его спектр.
 |
