Цветная сегментация изображения
Yining Deng, B. S. Manjunath andHyundoo Shin*
Статья взята с http://www-iplab.ece.ucsb.edu/publications/99CVPRSeg.pdf
Аннотация
В этой работе представлен новый подход к полностью автоматической цветной сегментации изображения, названный JSEG. Сначала цвета в изо-бражении квантуются и представляются несколькими классами, которые мо-гут быть использованы для того, чтобы дифференцировать области в изобра-жении. В результате цвет пикселя изображения заменяется соответствующи-ми метками цветных классов, формируя таким образом карту изображения. Предложен критерий «хорошей сегментации» при использовании указанной карты классов. Применение критерия к локальным окнам в карте классов приводит к "J-изображению", в котором высокие и низкие значения соответ-ствуют возможным границам области и центрам области, соответственно. Для сегментирования изображения, основанного на многошкальных J-изображениях, используется метод роста областей. Эксперимент показывает, что JSEG обеспечивает хорошие результаты сегментации различных изобра-жений.1. Введение
Цветная сегментация изображения используется для многих целей. В ре-зультате сегментации возможна идентификация интересующих областей и объектов в сцене, которые важны для последующего анализа изображения. В недавних работах используется различная техника: к примеру, стохастиче-ская модель базируется на подходах [1], [4], [8], [11], [12], морфологический водораздел, основывающийся на выращивании областей [9], энергетическая диффузия [7], и разделение диаграммы [10]. Количественные методы оценки были также предложены в [2]. Однако вследствие сложности проблемы, име-ется немного алгоритмов, которые могут работать при большом разнообра-зии данных.
Проблема сегментации трудна из-за текстуры изображения. Если изо-бражение содержит только однородные цветные области, методы кластериза-ции цветного пространства типа [3] достаточны для решения проблемы. В действительности, естественные сцены богаты цветом и текстурой. Трудно опознавать области изображения, содержащие цвето-текстурные карти-ны. Принятый в данной работе подход использует следующие допущения:
- Каждая область в изображении содержит однообразно распределенные цвето-текстурные картины.
- Информация о цвете каждой области изображения может быть пред-ставлена несколькими квантуемыми цветами, которые верны для большин-ства изображений естественной сцены.
- Цвета между соседними областями различны – это основное допуще-ние алгоритма цветной сегментации изображения.
Основные результаты этой статьи следующие:
Мы вводим новый критерий для сегментации изображения (Раздел 3). Этот критерий включает
минимизацию затрат по разделению изображения, основываясь на метках пикселя. Как
объясняется в разделе 2, метки пикселя получаются путем цветовой квантификации,
и возможно их расширение на другие особенности изображения.
Для достижения целей сегментации предложен практический алгоритм, называемый JSEG.
В разделе 3 вводится понятие «J-изображения». «J-изображение» соответствует измерению
локальной неоднородности изобра-жения с использованием различных шкал. Точки минимума
в изображении соответствуют однородным областям, а пики соответствуют потенциальным
границам. Алгоритм пространственной сегментации описан в разделе 4, с его помощью
происходит рост областей из точек минимума «J-изображений», и таким образом достигается
сегментация.
2. Критерии сегментации
Во-первых, цвета в изображении грубо квантуются, без значительного ухудшения качества цветов. Целью этого является извлечение нескольких цветов представления, которые могут дифференцировать соседние области в изображении. Как правило, для изображения естественных сцен, необходимы 10-20 цветов. Для процесса сегментации важно хорошее цветное квантова-ние. В нашем выполнении используется алгоритм перцепционного цветного квантования [5].
После квантования квантуемым цветам назначаются метки. После кван-тования, квантуемые цвета назначены метки. Цветной класс - набор пикселов изображения, квантуемых к тому же самому цвету. Цвета пикселя изобра-жения заменены их соответствующими цветными метками класса. Новое соз-данное изображение меток названо картой класса. Примеры картин классов приведены на рис.2, где значения меток представлены тремя символами: «*», «+» и «0». Необходимая цветная информация для сегментации извлечена и сохранена в простой карте класса после цветного квантования. Обычно, каж-дая область изображения содержит пикселы от малого подмножества цвет-ных классов, и каждый класс распределен в нескольких областях изобра-жения.
Карта класса может рассматриваться как набор пространственных точек данных, расположенных в 2D плоскости. Значение каждой точки - позиция пиксела изображения - 2D вектор (x, y). Эти точки данных классифицируют-ся, и каждая точке назначается метка, которая является значением карты класса в той позиции изображения. В последующем предложен критерий для "хорошей" сегментации, используя эти пространственные точки данных.

Рис.1. Схема JSEG-алгоритма
Для дальнейшего используем следующий подход к измерению J-критерия. Пусть Z будет набором всех N точек данных в карте классов, пусть z = (x,y), z принадлежит Z и m:

Предположим, что Z классифицируется в С классов. Пусть mi будет средним значением Ni класса точек Zi
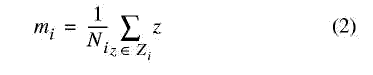
Пусть

и

Рис.2. Пример различных картин классов и их соответствующие J-значения, «*», «0» и «+», обозначающие три класса точек данных
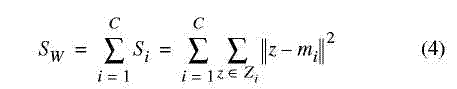
Измерение J определяется как

По существу, измеряются расстояния между различными классами SB по расстояниям между членами в пределах каждого класса; это подобно идее о линейной дискриминации множественных классов Фишера [6], но для произ-вольных нелинейных распределений класса. Более высокое значение J ука-зывает, что классы более отделены друг от друга, а члены внутри каждого класса более тесно связаны друг с другом, и наоборот.
Для случая, когда изображение состоит из нескольких однородных цветных областей, классы цветов в большей степени отделены друг от друга, и значение J велико. С другой стороны, если все классы цветов равномерно распределены по всему изображению, значение J невелико. В большинстве случаев значение J находится между вышеуказанными случаями. Например, на рис.2 показаны три карты классов, соответствующие трем упомянутым вариантам. Имеется три класса в каждой карте и число точек в каждом классе такое же самое для всех трех карт. Заметим, что значение J в этих трех случа-ях существенно различно.
Рассмотрим карту классов 1 на рис.2. «Хорошей» сегментаций в этом случае были бы три области, содержащие простые классы точек данных. Карта классов 2 является равномерно распределенной и сегментация не нуж-на. Для карты классов 3 «хорошей» сегментацией могут быть две области. Одна область содержит класс «+», а вторая содержит классы «*» и «0». Сег-ментация карты классов 1 и 3 показана на рис.3.
Теперь пересчитаем значение J по каждой сегментированной области вместо полной карты классов и определим среднее значение J

где Jk есть J, вычисленное по области k, Mk есть число точек в области k, N – общее число точек в карте классов, и суммирование проводится по всей об-ласти карты классов. Заметим, что J может рассматриваться как специальный случай J-среднего только для одной сегментированной области.

Рис.3. Сегментация карты классов и соответствующие значения J.
Теперь мы предлагаем использовать J-среднее как критерий минимиза-ции всех возможных всех возможных путей сегментации изображения. Для фиксированного числа областей, «лучшая» сегментация имеет тенденцию к более низкому значению J-среднего. Если сегментация является хорошей, каждая сегментированная область содержит небольшое число равномерно распределенных классов цветов и результирующее значение J для этой об-ласти невелико. Следовательно, полное значение J также невелико.
Значение J, вычисленное для карты классов 1 и 3, показано на рис.3. Яс-но, что в случае карты классов 1 все другие пути сегментации карты на три области приведут к значению J большему, чем в данном случае, поскольку J неотрицателен. То же самое верно и для карты классов 3, поскольку имеется большое число точек в карте, J{*,0} также приблизительно равно нулю. На уровне интуиции предположим, что границы сегментации изменены таким образом, чтобы одна область добавлена дополнительно к другой области. Значение J для вычитаемой (присоединенной) области остается равным ну-лю, тогда как значение J для другой области увеличивается вследствие появ-ления неоднородности. Таким образом, результатом новой сегментации бу-дет увеличение значения J.
3. J-изображения
Глобальная минимизация J-среднего для всего изображения является непрактичной. Однако заметим тот факт, что J, взятый из локальной области карты классов также является хорошим индикатором, если он относится к центру области или вблизи границ. Теперь мы введем понятие J-изображения:
J-изображение есть полутоновое (gray-scale) изображение, в котором значения пикселей есть J-значения, вычисленные по локальным окнам, цен-трированных на этих пикселях.
В оставшейся части статьи эти J-значения будут рассматриваться как локальные J-значения. Повышенное локальное J-значение наиболее вероятно обусловлено тем, что пиксель расположен поблизости от границы области. J-изображение подобно 3-D (трехмерной) карте поверхности, содержащей впа-дины и горы, фактически представляющие собой центральные области и об-ласти границ, соответственно.
Размер локального окна определяет размер областей изображения, кото-рые могут быть детектированы. Она небольшого размера полезныдля лока-лизации краев интенсивности/цвета, в то время как большие окна использу-ются для детектирования текстуры границ. Часто для сегментации изображе-ния необходимы множественные масштабы. В нашем случае основным ок-ном наименьшего масштаба является окно 9х9 без углов, как показано на рис.4 а. Углы удалены для того, чтобы сделать окно более округлым, так что выбор окна не имеет никакого отношения к прямоугольным объектам. Наи-меньший масштаб обозначается как масштаб 1. Начиная от масштаба 1, раз-мер окна удваивается каждый раз, чтобы получить следующий больший масштаб, как показано в табл.1.
По вычислительным причинам, очередность окон имеет нисходящий ха-рактер выбора. На рис 4 б показано окно, вдвое превышающее основное ок-но, или масштаба 2, где частота дискретизации 1 или 2 пикселя вдоль осей x или y. На рис.6 а показано исходное изображение видеосъемки (кадр 0) «цве-тущего сада». На этом же рисунке показано J-изображение в масштабе 3 (рис.6 c) и 2 (рис.6 d).
Таблица 1. Величина окна при различных масштабах
| Масштаб | Окно (пиксе-лей) | Выборка (1/пиксель) | Величина об-ласти (пиксе-лей) | Минимум точки минимума (пиксе-лей) |
|---|---|---|---|---|
| 1 | 9х9 | 1/(1х1) | 64х64 | 32 |
| 2 | 17х17 | 1/(2х2) | 128х128 | 128 |
| 3 | 33х33 | 1/(4х4) | 256х256 | 512 |
| 4 | 65х65 | 1/(8х8) | 512х512 | 2048 |
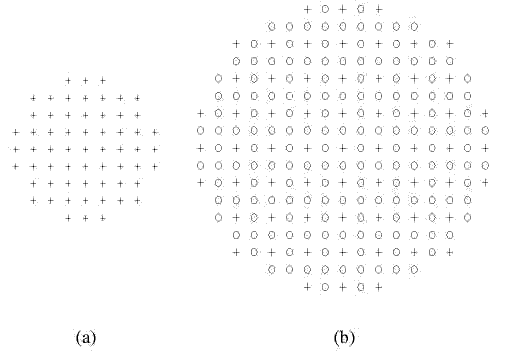
Рис. 4. (а) основное окно для вычисления J-значений, (б) иллюстрация нисходящего выбора (downsampling) для окна масштаба 2. Для вычисления локальных J-значений используются только «+» точки, фор-мирующие то же самое основное окно, что в случае (а)
4. Алгоритм пространственной сегментации
Характеристики J-изображения позволяют использовать метод роста об-ластей при сегментировании изображения. На рис.5 показана блок-схема по-следовательности выполнения разработанного нами алгоритма пространст-венной сегментации. Исходное изображение рассматривается как одна на-чальная область. Вначале алгоритм сегментирует все изображение с исполь-зованием первоначального большого масштаба. Этот процесс повторяется с уменьшением масштаба в отношении областей, сегментированных на преды-дущем шаге до тех пор, пока не будет достигнут минимальный установлен-ный масштаб.
В таблице 1 приведен набор масштабов и величин соответствующих этим масштабам областей, используемых для расчетов. Например, если вели-чина изображения больше, чем 256х256, но меньше, чем 512х512, стартовый масштаб равен 3. Пользователь определяет количество масштабов, необхо-димых для изображения, в результате определяется и минимальный масштаб, заканчивающий программу.
Фактически локальные J-значения вычисляются для каждой индивиду-альной области вместо полного изображения. Различия между ними и J-изображениями, рассмотренными в разделе 4 заключаются в том, что около границ области окна усечены согласно форме областей для того, чтобы избе-жать влияния границ соседних областей.
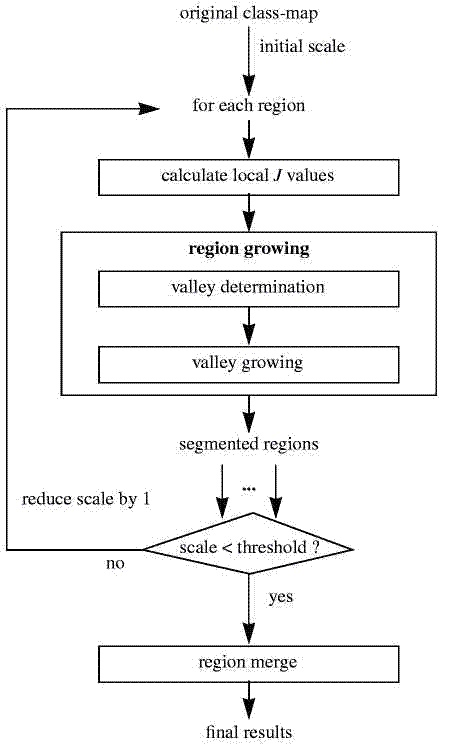
Рис.5. Блок-схема последовательности пространственной сегментации
4.1. Определение точки минимума
Вначале определяется набор небольших исходных областей, которые используются как основа для растущих областей. Эти области имеют самые низкие локальные J-значения и называются точками минимума. Вообще го-воря, нахождение наилучшего набора точек минимума области является не-тривиальной проблемой. Следующие простые эвристики позволяют получать хорошие экспериментальные результаты:
- Вычисляются средние величины и стандартные отклонения (диспер-сия) локальных J-значений
в области, обозначенные соответственно как
 и
и
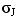 .
. - Устанавливается пороговое значение Т> при:

Пиксели с локальным значением J меньшим чем TJ рассматриваются как кандидаты на точки минимума. Соединение кандидатов на точки минимума основывается на 4-х связных соединениях. - Если кандидат на минимум имеет величину больше минимальной (имеется в виду размер окна?) величины, приведенной в табл.1 для соответ-ствующего масштаба, он определяется как минимальная точка.
-
 выбирается из набора значений [-0.6, -0.4, -0.2, 0, 0.2, 0.4], которые имеет наибольшее
число точек минимума.
выбирается из набора значений [-0.6, -0.4, -0.2, 0, 0.2, 0.4], которые имеет наибольшее
число точек минимума.
4.2. Рост точки минимума
Из точек минимума выращиваются новые области. Это медленный рост из точки минимума от пикселя к пикселю. Ускорение достигается путем ис-пользования следующих процедур:
- Удаление «дырок» из точек минимума.
- Усредняется локальное J-значение в оставшейся несегментированной области и соединяются пиксели с значением ниже среднего для фор-мирования области роста. Если растущие области соседствуют с од-ной и только одной минимальной точкой, она выбирается за точку минимума.
- Вычисляется локальное J-значение для оставшихся пикселей при следующем шаге уменьшения масштаба для более точной локализа-ции границ. Повторяется шаг 2.
- Выращиваются оставшиеся пиксели при наименьшем масштабе 1х1. Не расклассифицированные пиксели в точках минимума границ со-храняются в буфере. Каждый раз пиксель с минимальным J-значением относится к соседней точке минимума и буфер модифици-руется до тех пор, пока все пиксели не будут классифицированы.
4.3. Слияние области
После выращивания областей получается первоначальная сегментация изображения. При этом часто получаются излишне сегментированные облас-ти. Такие области необходимо объединить на основе их похожести. Кванто-вание цветов обычно реализуется в виде цветовой диаграммы. Извлекаются особенности цветовых диаграмм для каждой области и вычисляется расстоя-ние между этими особенностями. Поскольку цвета квантованы достаточно грубо, в нашем алгоритме предполагается, что они не коррелируют между собой. Поэтому Евклидово расстояние определяется непосредственным образом.
Для слияния областей используется метод агломератов [6]. Во-первых, вычисляется расстояние между двумя соседними областями и результат со-храняется в таблице. Пары областей, имеющие минимальное расстояние, сливаются вместе. Затем вычисляется вектор цветовых особенностей для но-вой области и расстояние в таблице модифицируется. Процесс продолжается до тех пор, пока не достигается заданное максимальное значение между об-ластями. После слияния получаем конечный результат сегментации.
5. Экспериментальные результаты
Алгоритм JSEG тестировался на разнообразных изображениях. На рис. 6 и 7 показаны результаты сегментации «цветущего сада» и исходные фото-графии. На сегментированных изображениях нельзя увидеть границы. Как видно, результаты довольно неплохие. Тем не менее, отсутствие базы для сравнения с другими методами не позволяет сделать объективную оценку метода.
В целом значения J подтверждают проведенное выше обсуждение и принятые допущения. Заметим, что на рис.6 значение J после сегментации при масштабе 2 становится больше значения J при масштабе 3 вследствие чрезмерной сегментации центральной области. Тем не менее, в конце, после слияния областей, достигается минимальное для всех вариантов значение J. Имеется несколько исключительных случаев, когда значение J больше для сегментированных изображений, чем исходных. Заметим, что цвета в этих изображениях более или менее симметричны относительно центра, что при-водит к малому значению J для исходного изображения. В этих случаях мо-жет помочь переопределение J в полярных координатах. Несмотря на некор-ректную индикацию значения J, результаты сегментации все еще хороши вследствие использования локальных значений J.
Алгоритм JSEG имеет три параметра, которые должны быть определе-ны пользователем. Первый из них - это порог (threshold) в процессе кванто-вания цветов. Он определяет минимальное расстояние между двумя квантуе-мыми цветами [5]. Второй параметр – это число масштабов, желательных для описания изображения в разделе 4. И последний – это порог при слиянии об-ластей. Эти параметры необходимы вследствие изменения характеристик изображения в различных прикладных случаях. Например, Для получения хороших результатов «цветущего сада» - изображения на рис.6, необходимо два масштаба.
Алгоритм хорошо работает с различными изображениями в случае ьис-пользования фиксированного набора значений параметров. На рис.7 показа-ны некоторые примеры из 2500 изображений, обработанных без дополни-тельной настройки индивидуальных изображений. Цветные изображения и все результаты расположены на сайте (http://vivaldi.ece.ucsb.edu/users/ deng/seg).
JSEG обеспечивает также хорошие результаты в случае использования полутоновых изображений, где значения интенсивности квантуются таким же самым образом, что и цвета. Эти результаты также расположены на сайте. Там же показаны примеры обнаружения иллюзорных контуров путем использова-ния черно-белого изображения для непосредственной обработки карты клас-сов.
6. Заключение
В данной работе представлен новый подход для полностью автоматиче-ской цветной сегментации изображения, названной JSEG. Сегментация вклю-чает цветное квантование и пространственную сегментацию. Предложены критерии «хорошей сегментации». Применение критериев к локальным окнам изображения позволяет получить в результате J-изображения, которые могут быть сегментированы с использованием метода мультимасштабного выращи-вания областей. Результаты показывают, что JSEG обеспечивает хорошую сегментацию различных цветных изображений.
В наших экспериментах найдены некоторые ограничения для алгоритма. Один из случаев, когда две области не имеют четкой границы - это небольшие ветки на рис.6. Другой случай – это наличие различных оттенков объекта вследствие изменения освещенности. К примеру, большой ствол дерева на рис.6 сегментирован на несколько частей вследствие изменения оттенков. Будущие исследования покажут, как решить эти проблемы и улучшить ре-зультаты.
References
[I] S. Belongie, et. al., "Color- and texture-based image segmentation using EM and its application to content-based image retrieval", Proc. oflCCV, p. 675-82, 1998.
[2] M. Borsotti, P. Campadelli, and R. Schettini, "Quantitative evaluation of color image segmentation results", Pattern Recogni¬tion letters, vol. 19, no. 8, p. 741-48, 1998.
[3] D. Comaniciu and P. Meer, "Robust analysis of feature spaces: color image segmentation", Proc. of IEEE Conf. on Com¬puter Vision and Pattern Recog-nition, pp 750-755, 1997. [4] Y. Delignon, et. al., "Estimation of generalized mix-tures and its application in image segmentation", IEEE Trans, on Image Process-ing, vol. 6, no. 10, p. 1364-76, 1997. [5] Y. Deng, C. Kenney, M.S. Moore, and B.S. Manjunath, "Peer group filtering and perceptual color image quantization", to appear in Proc. oflSCAS, 1999.
[6] R.O. Duda and RE. Hart, Pattern Classification and Scene Analysis, John Wiley & Sons, New York, 1970. [7] W.Y Ma and B.S. Manjunath, "Edge flow: a framework of boundary detection and image segmentation", Proc. ofCVPR, pp 744-49, 1997.
[8] D.K. Panjwani and G. Healey, "Markov random field mod¬els for unsupervised segmentation of textured color images", PAMI, vol. 17, no. 10, p. 939-54, 1995.
[9] L. Shafarenko, M. Petrou, and J. Kittler, "Automatic watershed segmentation of randomly textured color images", IEEE Trans, on Image Processing, vol. 6, no. 11, p. 1530-44, 1997.
[10] J. Shi and J. Malik, "Normalized cuts and image seg-menta¬tion", Proc. ofCVPR, p. 731-37, 1997.
[II] J.-P. Wang, "Stochastic relaxation on partitions with connected components and its application to image segmentation", PAMI, vol. 20, no.6, p. 619-36, 1998.
[12] S.C. Zhu and A. Yuille, "Region competition: unifying snakes, region grow-ing, and Bayes/MDL for multiband image segmentation", PAMI, vol. 18, no. 9, p. 884-900
Статья взята с www-iplab.ece.ucsb.edu