Цветная сегментация изображения с помощью глобальной инфор-мации и локальной однородности
Hanzi Wang and David Suter
Источник http://www.cmis.csiro.au/Hugues.Talbot/dicta2003/cdrom/pdf/0089.pdf
Аннотация
В этой статье предложен новый метод цветной сегментации изображе-ния с помощью глобальной информации и локальной однородности. В мето-де используется алгоритм сдвига среднего значения оттенка и интенсивности подпространства HSV. Рассматриваются также циклические свойства оттен-ков компонент в предложенном методе. Эксперимент с обычными цветными изображениями дает обещающие результаты.
1. Введение
Одной из наиболее значительных задач в распознавании образов явля-ется обработка изображений, в результате связанные участки сегментируют-ся в однородные области. Сегментация изображения является первым шагом на пути понимания и анализа изображения. Сегментация изображений при-знана одной из наиболее трудных задач в компьютерном зрении и обработке изображений [3,8]. В отличие от других задач зрения, таких как оценка пара-метрической модели [20,22], фундаментальной матричной оценки [18], пото-ком оптических вычислений [21] и т.п., нет общепринятых моделей или ана-литических решений для сегментации изображения. Этим вероятно, объясня-ется, не «одна истина» сегментации, принимаемая различными людьми и в различных психофизических условиях.
Набор предложенных методов сегментации, грубо говоря, может быть классифицирован следующим образом [3]: 1) гистограмма пороговой обра-ботки [13], кластеризация [6,23,2], 3) выращивание областей [1], основываю-щиеся на краях [14], основанные на физической модели [12], фаззи-подход и 7) нейросетевые методы.
Техника кластеризации выделяет однородные кластеры точек в про-странстве признаков (такие как RGB цветовое пространство, HSV цветовое пространство и т.п.) и метка каждого кластера рассматривается как отдельная область. Обычно используется критерий однородности, основанный на по-хожести цветов, т.е. расстояние от одного кластера до другого в пространстве цветовых признаков может быть меньше порогового. Недостатком этого ме-тода является то, что он не учитывает локальную информацию между сосед-ними пикселями.
В данной статье мы предлагаем метод сегментации, путем введения ло-кальной однородности в среднее значение алгоритма сдвига, используя и глобальную, и локальную информацию. Метод выполнен в двумерном под-пространстве «Оттенок – Значение» из пространства Оттенок - Насыщен-ность – Значение. По сравнению с предложенными алгоритмами сдвига среднего значения в LUV и RGB цветовом пространстве, сложность предло-женного метода ниже. В предложенном методе также предполагается рас-смотреть циклические свойства компонент окраски, использованием которых делает необязательным априорное знание числа кластеров и (облегчает?) по-иск незамеченных кластеров.
Статья организована следующим образом: в разделе 2 вводится HSV (цвет-насыщенность-значение) цветовое пространство; алгоритм среднего сдвига вводится в разделе 3. В разделе 4 излагается предлагаемый метод сег-ментации цветного изображения. Раздел 5 включает эксперименты по сег-ментации цветных (реальных) изображений. И заключение дается в разделе 6.
2. HSV цветовое пространство
RGB (красный, зеленый, синий) цветовое пространство широко ис-пользуется, но пространство HSV (оттенок (цвет)-насыщенность-значение) в некоторых случаях предпочтительнее (см. рис.1.). Оттенок определяет внут-ренние свойства света. Насыщенность описывает «насколько чистым являет-ся цвет». Последним компонентом тройки является измерение «насколько велика яркость цвета». Имеется также ряд вариантов HSV пространства: HSI (оттенок-насыщенность-интенсивность), HSB (оттенок-насыщенность-яркость) и HSL (оттенок-насыщенность-освещенность) [3]. HSV широко ис-пользуется в задачах компьютерного зрения [4,23,17]. Преимущества HSV над RGB следующие [4,3]:
- оттенок является инвариантом определенных типов освещенности, за-темнения и теней;
- сегментация, выполнения с использованием только одной размерно-сти (H), приводит в результате к меньшему количеству сегментов, чем при использовании RGB.
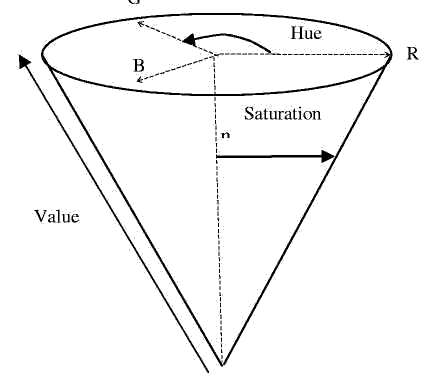
Рис.1. HSV цветовое пространство
Хотя авторы работы [4] использовали и оттенок, и интенсивность для сегментирования цветных изображений, они сегментировали цветное изо-бражение вначале в одноразмерном пространстве интенсивности затем, ие-рархически, сегментировали результаты (из сегментированного подпро-странства интенсивности) в подпространстве оттенков. Таким образом, это есть просто интенсивное сегментирование изображения. В данной статье мы используем алгоритм среднего сдвига в двумерном подпространстве оттенок-значение. Значение оттенка задано в диапазоне от 0 до 255. Поскольку значе-ние оттенка представляется углом, он имеет циклические свойства (см. под-разделы 3.3 и 4.2).
3. Алгоритм среднего сдвига
С тех пор как Fukunaga and Hostetler [10] ввели алгоритм среднего сдвига, он интенсивно используется и применяется в задачах низкоуровне-вого компьютерного зрения [5,7,8] вследствие легкости и эффективности. Одной из вектора среднего сдвига является то, что точка сдвига всегда сме-щается в направлении увеличения максимума интенсивности. Смещение центра (или окна) соответствует режиму или центру с высокой концентра-цией данных. Алгоритм среднего сдвига основан на ядре оценки плотности.
3.1. Алгоритм среднего сдвига и ядро оценки плотности
Пусть {Xi}i=1,…n есть набор n точек данных в d-размерном Евклидовом пространстве Rd , многомерное ядро оценки плотности с ядром К и окном радиусом (диапазон-ширина) h определяется следующим образом ([16], p.76):
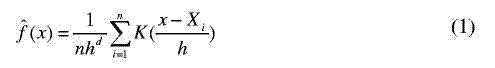
Ядро функции K(x) должно удовлетворять некоторым условиям ([19], p.95). Ядро Епанешникова ([16], p.76) есть оптимальное ядро, приводящее к минимуму среднеквадратичной ошибки (MISE):
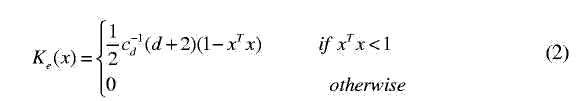
где cd есть объем единичной d-размерной сферы, т.е., с1=2, с2=?, с3=4?/3. Та-ким образом, плотность градиента оценки ядра Епанешникова может быть переписана как:
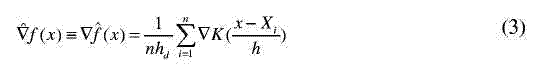
Уравнение (3) может быть переписано как:
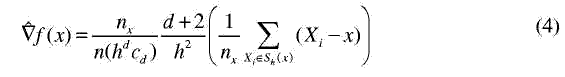
где область Sh(x) есть гиперсфера радиуса h, имеющая объем hd cd, центриро-ванный при х и содержащий nx точек.
Вектор среднего сдвига Mh(x) определяется как:

Из уравнений (4) и (5) получаем:

Уравнение (6) впервые было введено в работе [10]. Средний сдвиг есть неконтролируемая непараметрическая оценочная функция градиента плотно-сти, а средний вектор сдвига представляет собой разность между локальным средним значением и центром окна.
3.2. Процедура среднего сдвига
Алгоритм среднего сдвига может быть описан следующим образом:
- Выберите радиус окна поиска.
- Инициализируйте локализацию окна xk, k=1.
- Вычислите вектор сдвига Mh,k(xk).
- Переместите окно поиска путем вычисления xk+1=Mh,k(xk) + xk, k=k+1.
- Шаги 3 и 4 повторите до получения сходимости.
Средний сдвиг автоматически находит локальный максимум плотности. Это его свойство сохраняется даже в высоко размерных пространствах при-знаков.
В работе [4] авторы также предложили алгоритм нахождения пика. К со-жалению, он основан на эвристике. В отличие от него, алгоритм среднего сдвига имеет строгое теоретическое обоснование. Доказательство сходимо-сти алгоритма среднего сдвига может быть найдено в [7,8].
3.3. Циклические свойства компоненты оттенков в алгоритме сред-него сдвига
Вследствие того, что оттенок введен как значение угла, необходимо рассмотреть циклические свойства оттенков. Пересмотренный алгоритм среднего сдвига может быть переписан как:

где схождение (смещение?) окна с центром х есть вектор от [H,V],
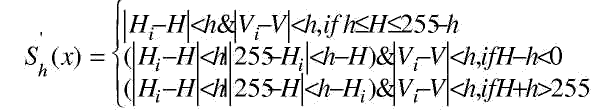
и nx есть число точек данных внутри гиперсферы Sh(x).
Пусть при смещении поискового окна xk+1=[Hk+1,Vk+1]. Тогда мы имеем:
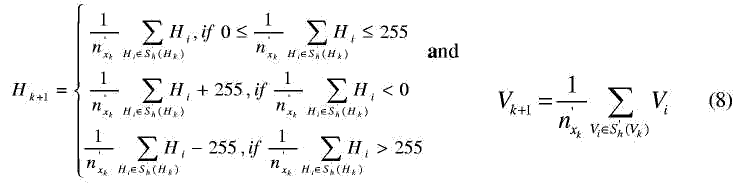
4. Предложенный метод сегментации цветных изображений
Хотя алгоритм среднего сдвига успешно использовался для кластери-зации [5,7], сегментации изображений [6,8], отслеживания [9] и т.д., он учи-тывает только глобальную информацию, пренебрегая локальной. В данной работе мы вводим понятие локальной однородности [4] в алгоритм среднего сдвига. Предложенный метод учитывает как глобальную информацию, так и локальную однородную информацию.
4.1. Локальная однородность
В [4] для измерения локальной однородности использовали однораз-мерную гистограмму пороговой обработки. Однородность определяется дву-мя составляющими: стандартным отклонением и разрывами интенсивности на каждом пикселе изображения. Стандартное отклонение Sij при пикселе Pij может быть записано как:
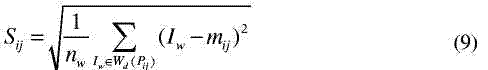
где mij есть среднее nw интенсивностей в окне Wd(Pij), имеющем величину d и центр в точке Pij.
Измерение разрыва Dij при пикселе Pij может быть записано как:

где Gx и Gy есть градиенты при пикселе Pij в х и у направлении.
Таким образом, однородность Hij при Pij может быть записана как:
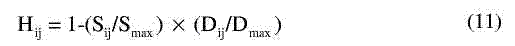
Из уравнения (11) видно, что значение H находится в диапазоне от 0 до 1. Чем выше значение Hij, тем более однородна область, окружающая пик-сель Pij.
В работе [4] авторы применили критерий однородности к гистограмме черно-белых уровней. В этой работе мы показываем, что локальная однород-ность может быть также включена в популярный алгоритм среднего сдвига.
4.2. Метод сегментации цветных изображений
Предложенный нами метод состоит в основном из трех частей:
- Отобразите изображение в пространстве признаков, учитывая как глобальную цветовую информацию, так и локальную однородность.
- Примените модифицированный алгоритм среднего сдвига (подраздел 3.3.) для получения пиков.
- В конце процесса присвойте пиксели каждому кластеру.
Детали описанного метода следующие:
- Отображение изображения в пространство признаков Вначале вычисляется локальное значение однородности для каждого пикселя изображения. Для вычисления стандартного отклонения каждого пикселя используется окно 5х5. Для оценки разрывов использовали окно 3х3. Конечно, могут быть использованы и другие размеры окон. Однако мы нахо-дим, что использованные в нашем случае окна обеспечивают лучшие харак-теристики и эффективность вычислений. После вычисления однородности для каждого пикселя мы использова-ли только пиксели с высоким значением однородности (близко к 1), и пре-небрегали пикселями с низким значением однородности. Мы отобразили пиксели с высоким значением однородности в двумерное пространство отте-нок-значение. Таким образом, учитывается как глобальная , так и локальная информация.
- Применение алгоритма среднего сдвига для нахождения локальных мод с высокой плотностью. Мы случайным образом инициализировали некоторые окна с радиусом h в HV пространстве. Выбирали окна, в которых число точек с данными было большим, а центр окна не находился поблизости с уже обработанными ок-нами. После того, как выбрано начальное окно, мы применяли алгоритм среднего сдвига для получения локальных пиков, при этом учитывались цик-лические свойства компоненты оттенков.
- Проверка правильности пиков и маркировка пикселей.
После применения алгоритма среднего сдвига мы получаем набор пи-ков. Очевидно, не все из этих пиков являются достоверными. Необходима некоторая итоговая обработка для подтверждения правильности пиков.
- Удаление повторяющихся пиков. Поскольку точность среднего сдвига ограничена, один и тот же пик, полученный средним сдви-гом, может не быть точно в том же положении. Таким образом, мы удаляем повторяющиеся пики, расположенные близко друг к другу (т.е. расстояние между ними менее 1.0).
- Удаляем пики, малые по сравнению с максимальными пиками. Это вызвано тем, что алгоритм
среднего сдвига может находить только локальные пики, и в связи с этим останавливается
и на малых ло-кальных пиках. Вычисляем нормализованный контраст и точки ми-нимума
между пиками:
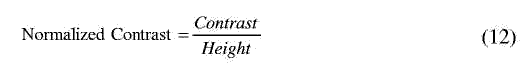
где контраст – это различие между малыми пиками и минимумами; вы-сота – значение меньшего из пиков. Если отношение (12) мало, удаля-ется меньший из пиков.
Таким образом можно удалить пики, полученные алгоритмом сдвига и находящиеся на локальном плато плотности вероятности.
После получения достоверных пиков, мы относим пиксели к ближай-шим кластерам. На этом шаге необходимо снова учесть циклические свойст-ва компоненты оттенков. Расстояние между i-th пикселем и j-th кластером есть:

где ? – фактор корректировки относительного веса компоненты оттенков, ис-ходя из значения компоненты.
Авторы [23] использовали k-алгоритм для сегментации изображения. Недостатком этого подхода является то, что пользователь должен задать чис-ло кластеров. В следующем разделе мы покажем преимущества предложен-ного метода.
5. Экспериментальные результаты сегментации цветных изображений
На рис.2 частично проиллюстрирован предложенный метод, а также приведены конечные результаты сегментации. Рис.2 (а) включает исходное изображение «дома». Точки в HV пространстве отображены на рис.2 (б) (без проведения достоверности локальной однородности) и на рис.2 (с) (после подтверждения локальной однородности). На рис.2 (d) показано отображение алгоритма среднего сдвига в HV пространстве для различных инициализа-ций. Синие линии – это следы процедуры среднего сдвига; зеленые точки – это центры смешенных путем процедуры среднего сдвига окон; и красные кружки – это конечные пики после подтверждения. На рис.2(е) даются ре-зультаты финальной сегментации по предложенному методу. Как можно ви-деть на рис.2(е), наш метод обеспечивает хорошие результаты сегментации. Дерево, дом, крыша, окно и периферия в нашем методе сегментированы от-дельно друг от друга. Окно и небо сегментированы в один и тот же кластер. Это связано с тем, что цвет окна голубой, подобно цвету неба. С точки зре-ния цветовой однородности, этот результат является корректным.
Можно также заметить, что поле сегментировано на две части: с одной стороны, можно сказать, что предложенный метод дает избыточный сегмент, поскольку оба сегмента принадлежат полю, а с другой, можно сказать, что метод корректно отображает поле, поскольку видно, что поле имеет разные цвета. Это вновь демонстрирует, что нет однозначного решения для сегмен-тации изображения.
На рис.4 мы сравниваем предложенный метод с методом, в котором использовалась подобная схема, но без учета локальной однородности и цик-лических свойств компоненты оттенков.
Можно видеть, что метод без учета локальной однородности и цикли-ческих свойств компоненты оттенков дает лишние сегменты и изображение «желе из шариков» разбито на семь цветов; голубые шарики разбиты на два кластера; часть красных шариков неправильно отнесена к черным. В проти-воположность этому, предложенный метод корректно сегментирует «желе из шариков» в пять цветов (пять цветов шариков и один цвет фона).
На рис.4 можно видеть, что метод без учета локальной однородности и циклических свойств компоненты оттенков дает лишние сегменты в изобра-жении «Всплеск». Красный фон разбивается на два кластера; также некото-рые пиксели красного фона неправильно отнесены к объекту на изображе-нии. В противоположность, предложенный метод дает хорошие результаты. Изображение эффективно сжато в три цвета.
6. Выводы
В данной статье новый метод цветовой сегментации изображения. Мы используем в нашем методе концепции однородности и алгоритма среднего сдвига. Таким образом, предложенный метод учитывает и локальную, и гло-бальную информации в процессе сегментирования изображения в однород-ные области. Изображение сегментируется в двухразмерном пространстве признаков оттенок-значение. Таким образом уменьшается вычислительная сложность по сравнению с методами LUV и RGB, в которых используется пространство признаков трех измерений. Циклические свойства компоненты оттенков учитываются в процедуре среднего сдвига и маркировке пикселей изображения. Эксперименты показывают, что предложенный метод перспек-тивен для сегментации естественных цветных изображений.

Рис. 2. (а) исходное изображение «дома»; (b) пространство признаков отте-нок-значение без учета локальной однородности; (с) пространство признаков с учетом локальной однородности; (d) процедуры и результаты разложения изображения алгоритмом среднего сдвига с различными инициализациями; (е) конечный результат с семи цветами, полученный предложенным методом при h=9.

Рис. 3. (а) Исходное изображение «Желе из шариков»; (b) конечный резуль-тат с пятью цветами, полученный предложенным методом при h=7; (с) ре-зультат с семью цветами без учета локальной однородности и циклических свойств оттенков (h=7).

Рис.4. (а) исходное изображение «Всплеск»; конечный результат с тремя цве-тами, полученный предложенным методом при h=7; (с) результат с шестью цветами, полученный без учета локальной однородности и циклических свойств оттенков (h=7).
Источник http://www.tip.csiro.au//dicta2003/