,
Источник: http://cache.rcom.ru/~dap/nneng/nnlinks/nbdoc/compare2.htm
В подразделе представлены результаты компьютерных экспериментов по обучению нейронных сетей с помощью следующих алгоритмов:
Одна из характеристик алгоритмов обучения - необходимое число дополнительных переменных при реализации алгоритма на компьютере. Основные переменные - это настраиваемые параметры сети (синаптические веса и смещения). Для организации вычислительного процесса и для хранения результатов промежуточных вычислений используются дополнительные переменные. При обучении нейронной сети с помощью некоторой программы и основные, и дополнительные переменные хранятся в оперативной памяти компьютера. Число основных переменных фиксировано, оно определяется числом настраиваемых параметров сети (весов и смещений). Число требующихся дополнительных переменных различно у разных алгоритмов. Объем оперативной памяти компьютера ограничен. Поэтому среди всех возможных алгоритмов обучения нейронных сетей необходимо выбирать те, которые требуют меньше всего дополнительных переменных. Число дополнительных переменных, которое требуется для реализации перечисленных выше алгоритмов на компьютере, не более чем в два раза превышает общее число настраиваемых параметров сети (синаптических весов и смещений).
В обобщенном градиентном алгоритме на каждой итерации выполняется вычисление градиента функции ошибки (определяются значения частных производных по синаптическим весам и смещениям) и делается шаг в направлении антиградиента. Величина шага задается пользователем.
Обобщенный градиентный алгоритм обучения в отличие от традиционного метода обратного распространения ошибки дает возможность обучать многослойные сети с произвольным числом слоев. Использование двойственных переменных ускоряет процесс обучения.
Градиентный алгоритм с автоматическим определением длины шага определяется следующим набором параметров:
В начале обучения с помощью автономного градиентного алгоритма записываются на диск значения весов и смещений сети. Затем происходит заданное число итераций обучения с заданным шагом. Если после завершения этих итераций значение функции ошибки не возросло, то шаг обучения увеличивается на заданную величину, а текущие значения весов и смещений записываются на диск. Если на некоторой итерации произошло увеличение функции ошибки, то с диска считываются последние запомненные значения весов и смещений, а шаг обучения уменьшается на заданную величину.
При использовании автономного градиентного алгоритма происходит автоматический подбор длины шага обучения в соответствии с характеристиками адаптивного рельефа.
В алгоритмах с одномерной оптимизацией адаптивный рельеф вдоль антиградиента функции ошибки аппроксимируется параболой. На каждой итерации выполняется два пробных шага: один в направлении антиградиента, другой - в противоположном направлении. По тем точкам (включая исходную точку итерации) строится парабола. Для параболы с лучами, направленными вверх, шаг делается в самую нижнюю точку. Если лучи параболы направлены вниз, то выполняется шаг в сторону антиградиента на заданную величину.
В алгоритме с одномерной оптимизацией и автоматическим определением длины шага выполняются действия, аналогичные автономному градиентному алгоритму. Величина пробных шагов подбирается под адаптивный рельеф.
В алгоритме поиска в случайном направлении на каждой итерации делается шаг, направление которого задается случайным образом. Если данный шаг приводит к увеличению функции ошибки, то происходит возврат к исходным значениям синаптических весов и смещений и выполняется шаг в другом случайном направлении.
Алгоритм имитации отжига является в настоящее время одним из самых популярных алгоритмов для решения задач оптимизации. Прежде всего он используется для размещения микросхем на печатных платах. В литературе отмечается успешное использование алгоритма для обучения нейронных сетей малой размерности - с числом синаптических весов и смещений порядка нескольких сотен.
В алгоритме итерации выполняются случайным образом с учетом ограничений на значения настраиваемых параметров. Причем допускаются шаги, приводящие к увеличению функции ошибки. Пусть на итерации k нейронная сеть находится в точке адаптивного рельефа, характеризующейся значением функции ошибки D. Шаг из точки S в точку S' со значением функции ошибки D' (D>D'), приводящий к увеличению значения функции ошибки на величину (D'-D), допускается с вероятностью:
,
где T(k) - значение температуры на шаге k. Значение температуры убывает с течением времени:
.
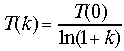В таблице 3.1 представлены характеристики описанных алгоритмов:
Таблица показывает, что наиболее эффективным является автономный градиентный алгоритм. Стохастические методы (поиск в случайном направлении и метод отжига) сходятся крайне медленно при обучении нейронных сетей больших размерностей - несколько тысяч и больше настраиваемых параметров.
Данные, аналогичные приведенным в таблице, были получены при обучении нейронных сетей для решения задач распознавания и адаптивного управления.
Далее на рисунках представлены графики функции ошибки перечисленных выше алгоритмов с различными значениями параметров.
На графиках функции ошибки алгоритмов с автоматическим определением длины шага видны характерные пилообразные участки с уменьшающейся высотой пиков.
Таблица 3.1
|
N |
Название алгоритма обучения |
Один шаг, сек |
Количество шагов решения контрольной задачи |
Объем вычислений |
| 1 | Обобщенный градиентный алгоритм |
2.02 |
715 |
2.08 |
| 2 | Градиентный алгоритм с автоматическим определением длины шага (автономный градиентный алгоритм) |
2.03 |
342 |
1.00 |
| 3 | Алгоритм поиска в случайном направлении |
1.64 |
52700 |
124.48 |
| 4 | Градиентный алгоритм с одномерной оптимизацией |
6.85 |
206 |
2.03 |
| 5 | Градиентный алгоритм с одномерной оптимизацией и с автоматическим определением длины шага |
5.34 |
290 |
2.23 |
| 6 | Имитация отжига |
1.64 |
32576 |
76.95 |
Приведенные графики показывают, в частности, что обобщенный градиентный алгоритм очень чувствителен к значению шага. Так, при величине шага 0.2 алгоритм не сходится. После первых семидесяти шагом обучения функция ошибки перестает уменьшаться, хотя сеть еще не приобрела способность правильно распознавать хотя бы один образ из обучающей выборки. График показывает, что на нескольких итерациях обучения функция ошибки резко возрастала. При шаге 0.1 процесс обучения стабильно сходился к локальному минимуму функции ошибки. Оказавшись в этом локальном минимуме, сеть приобретает способность распознавать все образы из обучающей выборки.
При обучении по градиентному алгоритму с автоматическим определением длины шага (автономному градиентному алгоритму) на графиках функции ошибки видны характерные пилообразные участки с уменьшающейся высотой пиков. Эти участки соответствуют процессу подстройки длины шага алгоритма под локальные характеристики адаптивного рельефа. За счет использования процедуры подстройки величины шага удается достичь значительного ускорения процесса обучения. В отличие от алгоритмов с одномерной оптимизацией, процедура настройки шага в автономном градиентном алгоритме предельно проста, не требует значительных вычислительных затрат. Поэтому, хотя общее число итераций при обучении сети с помощью автономного алгоритма больше, чем при обучении той же сети по алгоритму с одномерной оптимизацией, в целом обучение завершается быстрее.
Хотя автономный градиентный алгоритм дает возможность подбирать значение шага под адаптивный рельеф в локальной области, скорость сходимости зависит от параметров алгоритма. Так при обучении двухслойной сети распознаванию изображений
наибольшая скорость сходимости достигается при начальном значении шага 0.1, запоминание параметров сети производится через 10 шагов, изменение шага 10%.
Из всех рассмотренных алгоритмов наименьшей скоростью сходимости обладает алгоритм поиска в случайном направлении. Для того, чтобы в соответствии с алгоритмом поиска в случайном направлении сделать шаг по адаптивному рельефу, уменьшающий функцию ошибки, необходимо совершить множество пробных шагов. Скорость сходимости зависит от величины шага. В экспериментах наибольшая скорость сходимости достигалась при шаге 0.1.
Из всех алгоритмов, реализованных в программе "Нейроэмулятор 2.6", градиентные алгоритмы с одномерной оптимизацией сходятся к локальному минимуму за наименьшее число шагов. Однако на каждом шаге выполняется большой объем вычислений. Поэтому выигрыша во времени всего процесса обучения не происходит.
Рис. 3.1. Функция ошибки алгоритма поиска в случайном направлении
(шаг 0.01, на графике представлено 120 итераций)
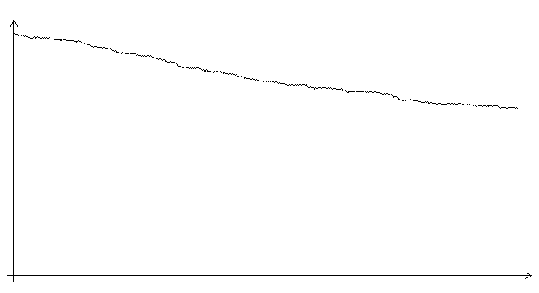
Рис. 3.2. Функция ошибки алгоритма поиска в случайном направлении (шаг 0.01, на графике представлено 600 итераций)
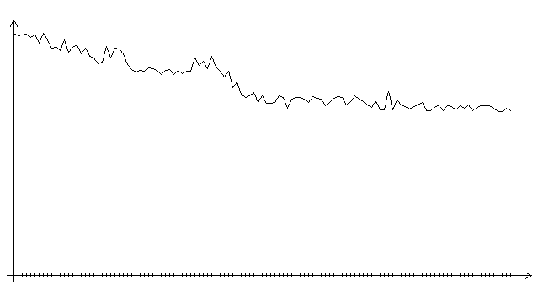
Рис. 3.3. Функция ошибки алгоритма поиска в случайном направлении (шаг 0.1, на графике представлено 120 итераций)
Рис. 3.4. Функция ошибки алгоритма поиска в случайном направлении (шаг 0.1, на графике представлено 600 итераций)
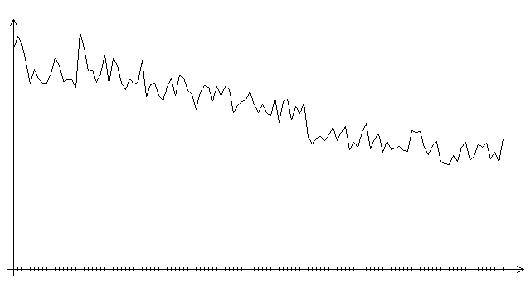
Рис. 3.5. Функция ошибки алгоритма поиска в случайном направлении
(шаг 1.0, на графике представлено 120 итераций)
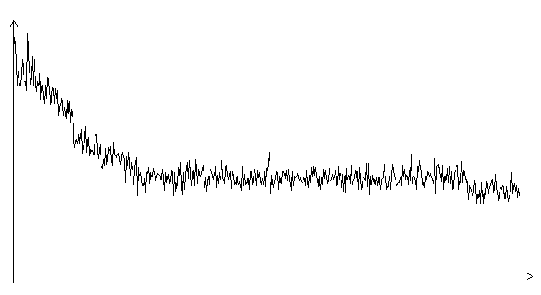
Рис. 3.6. Функция ошибки алгоритма поиска в случайном направлении
(шаг 1.0, на графике представлено 600 итераций)
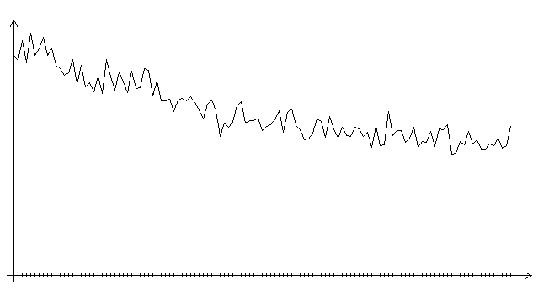
Рис. 3.7. Функция ошибки алгоритма поиска в случайном направлении
(шаг 10.0, на графике представлено 120 итераций)
Рис. 3.8. Функция ошибки алгоритма поиска в случайном направлении (шаг 10.0, на графике представлено 600 итераций)
Рис. 3.9. Функция ошибки автономного градиентного алгоритма (начальное
значение шага 0.1, запоминание через 10 итераций, изменение шага на 10%, на графике
представлено 120 итераций)
Рис. 3.10. Функция ошибки автономного градиентного алгоритма (начальное значение шага 0.1, запоминание через 10 итераций, изменение шага на 10%, на графике представлены итерации с 3 по 140)
Рис. 3.11. Функция ошибки автономного градиентного алгоритма (начальное
значение шага 0.1, запоминание через 10 итераций, изменение шага на 10%, на графике
представлены итерации с 3 по 295)
Рис. 3.12. Функция ошибки автономного градиентного алгоритма (начальное значение шага 0.1, запоминание через 10 итераций, изменение шага на 10%, на графике представлены итерации с 3 по 600)
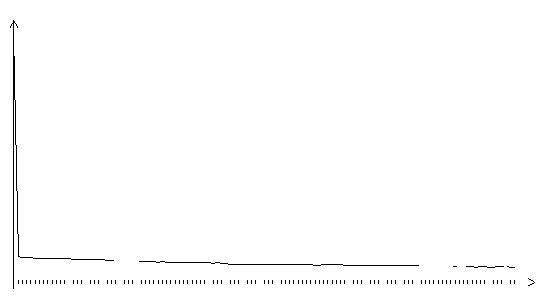
Рис. 3.13. Функция ошибки обобщенного градиентного алгоритма (шаг
0.01, на графике представлено 120 итераций)
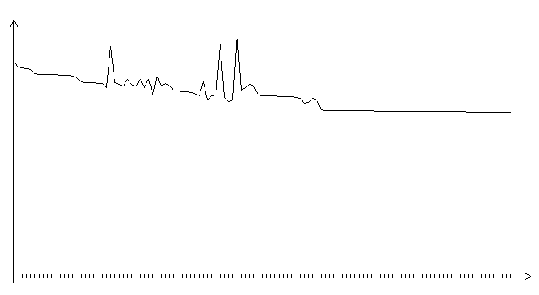
Рис. 3.14. Функция ошибки обобщенного градиентного алгоритма (шаг
0.2, на графике представлено 120 итераций)
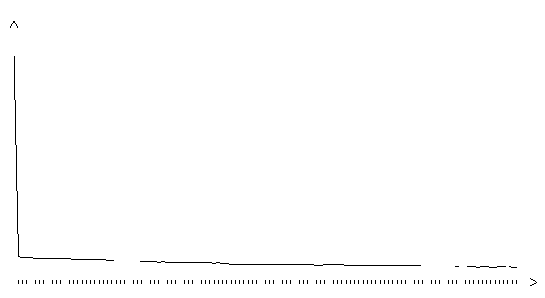
Рис. 3.15. Функция ошибки обобщенного градиентного алгоритма (шаг
0.1, на графике представлено 120 итераций)
Рис. 3.16. Функция ошибки обобщенного градиентного алгоритма (шаг
0.1, на графике представлены итерации с 2 по 600)
Рис. 3.17. Функция ошибки обобщенного градиентного алгоритма (шаг 1.0, на графике представлено 120 итераций)
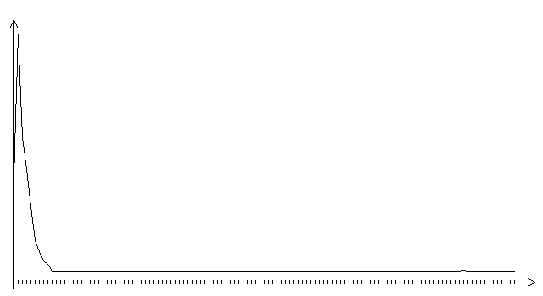
Рис. 3.18. Функция ошибки обобщенного градиентного алгоритма (шаг
10.0, на графике представлено 120 итераций)
Рис. 3.19. Функция ошибки градиентного алгоритма с одномерной оптимизацией (шаг 0.001, на графике представлено 120 итераций)
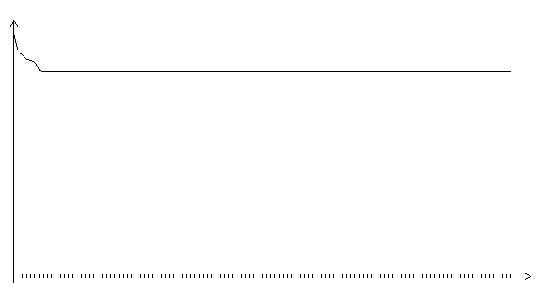
Рис. 3.20. Функция ошибки градиентного алгоритма с одномерной оптимизацией
(шаг 0.1, на графике представлено 120 итераций)
Рис. 3.21. Функция ошибки градиентного алгоритма с одномерной оптимизацией (шаг 0.01, на графике представлено 120 итераций)
Рис. 3.22. Функция ошибки градиентного алгоритма с одномерной оптимизацией (шаг 0.01, на графике представлено 600 итераций)
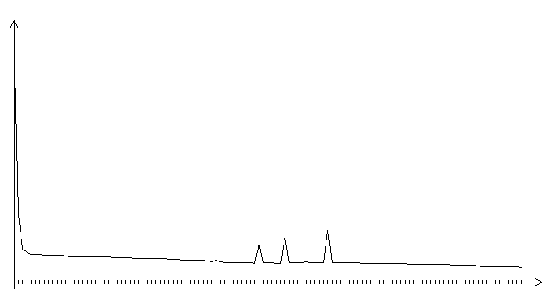
Рис. 3.23. Функция ошибки градиентного алгоритма с одномерной оптимизацией и автоматическим определением длины шага (начальное значение шага 0.01, запоминание через 5 итераций, изменение шага на 10%, на графике представлено 120 итераций)
|
При использовании информации, находящейся на данной странице, вы
обязаны ссылаться на следующую работу:
Отчет по научно-исследовательской работе "Создание аналитического обзора информационных источников по применению нейронных сетей для задач газовой технологии"; Копосов А.И., Щербаков И.Б., Кисленко Н.А., Кисленко О.П., Варивода Ю.В. и др., ВНИИГАЗ, 1995. |