Most weather forecasts today are based on the output of complex computer programs, known as forecast models, which typically run on supercomputers and provide predictions on many atmospheric variables such as temperature, pressure, wind, and rainfall. A forecaster examines how the features predicted by the computer will interact to produce the day's weather.

Types of interactions considered in a weather forecast Model

Numerical models of weather (and climate as well) are based on the fundamental mathematical equations which describe the physics and dynamics of the movements and processes taking place in the atmosphere, the ocean, the ice and the land. Some of these processes are shown schematically in the figure above.

These models are:

• Very complex
• Deal with huge quantity of data
• Require a very large number of calculations

Therefore, these models need fast computers with large memory systems.

A 10-day weather prediction takes roughly 4 hours to complete.

First, the individual elements that make up the model must be specified along with measurable quantities that define the state of each element.

The state of each element, or block, in our model is specified for a given instant of time by a series of numbers that define its temperature, pressure, density, humidity, wind direction and speed, and so on. The diagram below gives you shows you what is meant by individual blocks (or grid cells) within the model. (NOTE: please ignore the text and boxes underneath the diagram. It is part of the image I found and difficult to cut out.)

We begin the operation of our model by specifying all these numbers for every block in the model. This is the initial condition of the model and defines the state of the model at the starting time.

Once these calculations are completed, we have a slightly changed model from the initial condition. Each block has updated values defining its temperature, pressure, density, humidity, wind direction and speed, and so on.

We can then repeat the process, calculating a new set of changes based on the new state of the model. What we end with is a numerical model that evolves with time, hopefully mirroring changes that take place in the actual atmosphere. In this class we have looked at forecasts of the 500 mb height pattern. The forecast can be judged by how well the true 500 mb height pattern (at the forecast time) compares with the original forecast.

State of the atmosphere at time t temperature, winds, etc.

equations that describe the behavior of the atmosphere

State of the atmosphere at time t + dt temperature, winds, etc.

equations that describe the behavior of the atmosphere

State of the atmosphere at time t + 2 * dt temperature, winds, etc.

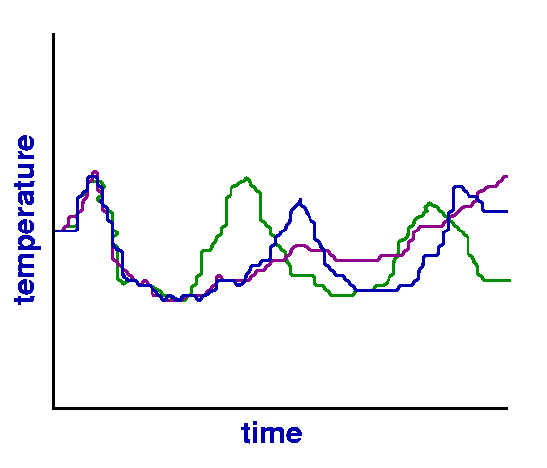
Specifying Initial Conditions

The model forecast must begin with a "known state" of the atmosphere, which is called the initial condition. Most of the information for the initial conditions comes from measurements of the state of the atmosphere. Twice each day, at 00Z and 12Z, weather observing stations launch weather balloons, which carry instruments upward taking measurements of temperature, pressure, winds, humidity, etc. Measurements taken by satellites are also used. The information from around the world is gathered and used to set or initialize the current state of the atmosphere. For example, the measured height of the 500 mb pressure level, taken all over the world, is used to construct the 500 mb height maps we have been looking at.

After gathering all of the observations, the model is run forward in time as discussed above.

Errors in Numerical Forecasts

Unfortunately due to the complexity of the atmosphere, numerical weather forecasts are not exact. There are two main reasons for this. First, the equations used by the models to simulate the atmosphere are not precise. Many processes in the atmosphere are either not fully understood or too complex to model with current computing power. Secondly, the initial conditions are not exact. All measurements have errors. In addition, there are gaps in the initial data since there are many places on Earth where there are no weather observation stations, such as over oceans or unpopulated land areas. Thus, even if the model equations were perfect, if the initial state is not completely known, the computer's prediction of how that initial state will evolve will not be entirely accurate.

The Earth's atmoshere is a chaotic system, which means that the future state of the system (which is what the model is trying to predict) is highly sensitive to the initial conditions. We know this is true because the same model, run with slightly different initial conditions, will give similar forecasts for the first couple of days, but wildly different forecasts beyond one week into the future (see figure below). In other words, unavoidable errors in specifying the initial conditions tend to amplify with time.

Simple representation of model sensitivity to initial conditions. Suppose we are just looking at the model forecast of temperature for a single location. The three different colors represent forecasts made using the same model, but with slightly different initial conditions. Over the short-term all three model runs make about the same forecast. But at longer forecast times, the three predictions diverge from each other.

Research shows that beyond about 10 days, numerical forecasts models have no skill in predicting weather, that is, you could guess the weather 10 days from now as well as it can be predicted by current forecast models. The forecasts are very good in the short term (1-3 days), still decent out to about 5 days, but degrade quickly after that.

Dilemma for Weather Forecasters

The public expects precise weather forecasts. As described above, numerical weather forecasts, which are the best we can do, are inherently uncertain. To make matters more confusing, there are dozens of weather forecast models run each day, and each one gives a different forecast. The local weather forecaster will often look over a bunch of models, then add in his knowledge of local weather pecularities, to come up with his individualized forecast. You should expect good short term forecasts and rather poor long range forecasts because that is the best that we can do today. It is not always because the forecaster does not know what he is doing. There is a limit to how well the future state of the atmosphere can be predicted.

A Helpful Analogy (hopefully)

Some people are surprised that it is so difficult to predict the weather. They figure that if we spend enough research time and money, we should be able to improve indefinitely, but this is not true. For any chaotic system, there are inherent limitations on the predictability of future states.

Consider the problem of predicting the path of a boulder that we push off the top of a hill. Some of the initial conditions for this problem include the direction in which we push the boulder, the weight of the boulder, the shape of the boulder, how hard we push it, and the precise condition of the hilly terrain (e.g., slope, small rocks in the way, small twigs, clumps of vegetation, etc.). Can we expect to know the initial conditions well enough to capture all the possible ways the path of the boulder can be changed? Probably not. This is in spite of the fact that the equations of motion, which govern the movement of the boulder as it rolls down the hill, are known very well. At first our prediction of the path of the boulder would be very good given that we know which way we pushed it, we know the direction it starts moving. As the boulder rolls down, though, it comes to places where it will hit an obstruction. If it hits on one side of the obstruction, the boulder makes a left turn, a few millimeters to the other side of the obstruction and the boulder makes a right turn. The future movement of the boulder beyond this obstruction depends critically on whether the boulder took a left turn or a right turn after hitting it. This depends on knowing the initial condition of the hill precisely, which we do not. Slight misrepresentations of the initial conditions cause errors which diverge over time. In fact if the hill is very high, our model may have no skill in being able to predict exactly where the boulder will be when it gets to the bottom of the hill. (Think about the Plinko game on the Price is Right). Predicting the future state of the atmosphere is certainly more complicated than the boulder problem.