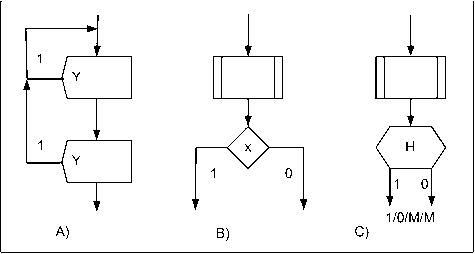
Аноприенко А.Я.

В условиях интенсивного развития распределенных сетевых и многопроцессорных вычислительных структур все более остро проявляется существенная ограниченность возможностей современной бинарной логики и алгоритмов на ее основе в адекватном отражении всей сложности реального мира. Практически уже назрела необходимость очередного качественного скачка в развитии в логико-алгоритмического базиса вычислительных процессов (см., например, [1]), и в первую очередь это актуально для вычислительного моделирования, где имеющиеся ограничения ощущаются наиболее явно. В работе [2] на основе анализа закономерностей кодо-логического базиса компьютерного моделирования было сделано заключение, что одним из наиболее перспективных направлений дальнейшего развития является переход к использованию гиперлогики и гиперкодов. В настоящей статье данные идеи впервые излагаются применительно к развитию алгоритмического базиса вычислительного моделирования.

От моноалгоритмов к классическим диалгоритмам

Аналогично развитию кодо-логического базиса в алгоритмической эволюции также могут быть выделены три основных этапа (рис. 1): моноалгоритмы (архаичный этап) на основе монологики и монокодов, диалгоритмы (современный этап) на основе дилогики и дикодов, гипералгоритмы на основе различных вариантов гиперлогики и гиперкодов (перспективный этап).

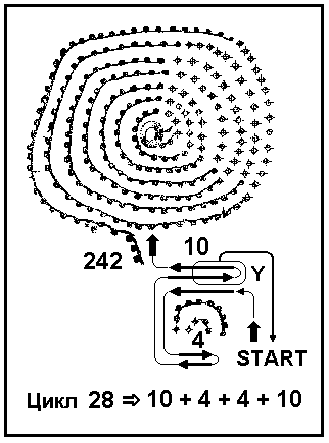
В работе [2] отмечалось, что в алгоритмическом плане монологике соответствует простая последовательность операторных вершин, выполнение которой реализуется в соответствии с правилом “если выполнен текущий оператор, то переходи к выполнению следующего”. Из логических операций с монологикой уверенно может быть связана лишь импликация (лат. Implicatio - сплетение), соответствующая связке “если..., то ...” и реализуемая в современных алгоритмических языках в виде условного оператора IF … THEN . Типичный моноалгоритм носит инкрементный характер, заключающийся в последовательном переборе некоторого конечного счетного множества. При этом на каждом шаге может проверяться некоторое моноусловие Y , наличие которого ведет к изменению заданной последовательности шагов и переходу в некоторую заданную вершину алгоритма, которой, как правило, является начальная вершина. Характерный пример реализации моноалгоритма показан на рисунке 2. Этот пример особенно интересен по той причине, что Мальтинская пластина, на которой он реализован, - это на сегодня практически древнейший (около 20-ти тысяч лет!) из известных образцов вычислительных моделирующих сред, реализованных на основе монокода [3, 4]. В числе прочих циклических процессов, отслеживаемых с помощью монокодовых узоров пластины, одним из наиболее интересных с алгоритмической точки зрения является 28-дневный репродуктивный цикл, длительность которого может существенно варьировать в зависимости от конкретной ситуации и индивидуальных особенностей. Учесть эту вариабельность позволяет возможность немедленного перехода в начальное состояние START при наступлении события Y , означающего окончание очередного цикла и начало следующего. Так как вариабельность цикла находится в пределах примерно 5-ти дней в сторону его сокращения или удлинения, то условие Y учитывается и действует фактически только в правой части участка «10». Регулярное наступление события Y является основным условием цикличности алгоритма, и в случае его отсутствия алгоритм «по умолчанию» переходит в длинную спиральную часть «242» монокодового узора. В целом, для моноалгоритмов значимым является только наличие (или появление) некоторого условия. Факт же отсутствия соответствующего условия специально не проверяется и приводит к реализации алгоритма в варианте «по умолчанию».

Переход к диалгоритмам может быть однозначно связан с введением в математическую символику специального обозначения для «нуля», позволившего в явном виде обозначать и проверять не только наличие чего-либо, например логического условия, но и его отсутствие. Само понятие «цифра», характерное именно для дикодов, обязано своим происхождением как раз первичному названию «нуля». Известный итальянский математик Леонардо Пизанский (Фибоначчи) в своем сочинении "Liber abaci" (1202) писал: "Девять индусских знаков - суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С помощью этих знаков и знака 0, который называется по-арабски zephirum, можно написать какое угодно число" (цитируется по работе [5]). Словом "zephirum" Фибоначчи передал арабское "as-sifr" , являющееся дословным переводом индусского слова "sunya", то есть "пустое", служившее названием нуля. Слово "zephirum" дало начало французскому и итальянскому слову "zero" (нуль). С другой стороны, то же арабское слово "as-sifr" было передано через "ziffer", откуда произошли французское слово "chiffre", немецкое "ziffer", английское "cipher" и русское "цифра". Фактически Фибоначчи введением «нуля» положил также начало и двоичной системе счисления, сформулировав в книге "Liber abaci" т.н. "задачу о выборе наилучшей системы весовых гирь для взвешивания грузов на рычажных весах". Известный немецкий математик Лейбниц (1646-1716), разработавший в 1697 г. правила двоичной арифметики, подчеркивал, что "вычисление с помощью двоек, то есть 0 и 1,… является для науки основным и порождает новые открытия, которые оказываются полезными впоследствии, даже в практике чисел, а особенно в геометрии: причиной чего служит то обстоятельство, что при сведении чисел к простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок" (цитируется по работе [5]). Двоичная система является фактически наиболее простым и наглядным вариантом реализации позиционных дикодов. Дилогике соответствует явное или неявное использование связки “если... то... иначе…”, реализуемой в современных алгоритмических языках в виде условного оператора IF … THEN … ELSE .

От диалгоритмов к гипералгоритмам и динамическому параллелизму

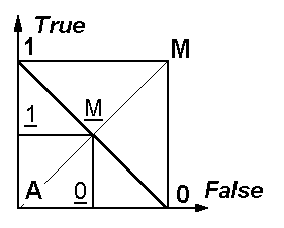
Использование различных вариантов гиперлогики для качественного скачка в развитии алгоритмического базиса современных вычислений и компьютерного моделирования созрело и концептуально, и технически в последние десятилетия, когда выявилась явная недостаточность классических моделей Тьюринга и Неймана, ориентированных исключительно на последовательные вычисления. Стремительное расширение сфер применения компьютерных технологий настоятельно потребовало нового уровня адаптации кодо-логического и алгоритмического базисов к реальной сложности окружающего мира, связанного в том числе с переходом к не-неймановской модели вычислений, предполагающей интенсивное использование различных форм параллелелизма [6]. При этом, если на раннем этапе речь шла преимущественно о статическом параллелелизме, основанном на матрично-векторных вычислениях в рамках уравнение-ориентированных моделей и функциональном параллелелизме в рамках блочно-ориентированных моделей, то в настоящее время особую актуальность приобретает динамический параллелелизм, базирующийся на многозадачной инфраструктуре программного обеспечения и развитой сетевой инфраструктуре аппаратных средств. При этом традиционные условные вершины бинарных (дилогических) алгоритмов превращаются в состояния (алгоритмические узлы), порождающие и/или уничтожающие параллельные процессы. Одним из простейших вариантов реализации таких узлов является функционирование их на основе тетралогики с состояниями 1, 0, М и М (рис. 3) [7], где М означает равновероятный переход на одну из ветвей 1 или 0, а состояние М означает порождение 2-х параллельных процессов, соответствующих ветвям 1 и 0 (рис. 1). Использование состояния А вместо М может означать отсутствие процессов на обоих ветвях, т.е. терминирование существующего процесса на входе узла. Наиболее общим случаем будет реализация непрерывной логики на всем пространстве между вершинами 1, 0, A и М. При этом могут реализовываться следующие 4 варианта организации параллельных процессов:

• легковесные (т.е. в общем адресном пространстве) процессы в рамках специализированных сред, например, на базе виртуальной Java -машины;
• легковесные процессы на базе возможностей непосредственно операционной системы, например, т.н. нити в рамках операционных систем семейства MS NT /2000/ XP ;
• полновесные (т.е. реализуемые в собственном защищенном адресном пространстве) процессы в рамках любой из многозадачных операционных систем, реализуемых на одном процессоре;
• полновесные процессы на различных процессорах и/или хост-компьютерах в параллельных и сетевых средах.

Последний вариант представляет наибольший интерес, т.к. в этом случае могут быть задействованы самые разнообразные варианты сетевого взаимодействия [8], в т.ч. механизмы сокетов, передачи сообщений, удаленного вызова процедур, технологии CORBA [9] и т.п.

Заключение и перспективы исследований

Таким образом, в настоящее время созрели все предпосылки для реализации и широкого использования т.н. гипералгоритмов, что можно рассматривать как первый этап более общего перехода к гиперлогике и гиперкодам. На практике это означает возможность эффективной реализации различных видов динамического параллелелизма, что в первую очередь актуально для распределенного моделирования сложных динамических процессов и систем, где сложность реального моделируемого мира оказывает наиболее непосредственное влияние на развитие вычислительных методов, структур и алгоритмов.

Литература

•  Кулик Б.А. С чем идет логика в XXI век? // Вестник Российского фонда фундаментальных исследований, № 3, сентябрь 2000 г. ( http://www.rfbr.ru/default.asp?doc_id=4767 )

•  Аноприенко А.Я. Расширенный кодо-логический базис компьютерного моделирования // Научные труды Донецкого государственного технического университета. Выпуск 1. Серия “Информатика, кибернетика и вычислительная техника» (ИКВТ-97). Донецк: ДонГТУ. – 1997. - С. 59-64.

•  Anoprienko A. Interpretation of some artefacts as special simulation tools and environments / “Short Papers Proceedings of the 1997 European Simulation Multiconference ESM'97. Istanbul, June 1-4, 1997" - Istanbul, SCS, 1997, p. 23-26.

•  Аноприенко А. Я. Восхождение интеллекта: эволюция монокодовых вычислительных моделей // Научные труды Донецкого государственного технического университета. Выпуск 15. Серия “Информатика, кибернетика и вычислительная техника» (ИКВТ-2000). - Донецк: ДонГТУ. – 2000. - С. 36-47.

•  Стахов А. Компьютер Фибоначчи (http://www.ssga.ru/erudites_info/computers/kompfib.html).

•  Бройнль Т. Паралельне програмування / Вступ. слово А.Ройтера; пер. з нім. В.А.Святного. – К.: Вища школа., 1997. - 358 с.

•  Anoprienko A. Tetralogic and tetracodes: an eff ective method for information coding // 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics. Berlin, August 24-29, 1997. Vol. 4. Artificial Intelligence and Computer Science. - Berlin: Wissenschaft und Technik Verlag. - 1997. - P. 751-754.

•  Аноприенко А.Я., Забровский С.В., Каневский А.Д. Опыт реинжиниринга системы моделирования сложных технологических процессов / Наукові праці Донецького державного технічного університету. Серія “Обчислювальна техніка та автоматизація”, випуск 20. - Донецьк, ДонДТУ, 2000, с. 139-148.

•  Аноприенко А.Я., Забровский С.В., Потапенко В.А. Использование технологии CORBA в распределенном моделировании сложных технологических систем / Наукові праці Донецького державного технічного університету. Серія “Обчислювальна техніка та автоматизація”. Випуск 38. - Донецьк, ДонДТУ, 2002, с. 186-190.

Сохранить(29кб)