| Биография |
ДонНТУ >
Портал магистров ДонНТУ |
| Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание | |
Арифметическое кодирование
Сопоставим каждой последовательности бит множество всех вещественных чисел, лежащих в интервале [a; b). Разным файлам будут соответствовать различные интервалы.
Разобьем исходную последовательность на отдельные элементы так, чтобы по ним можно было ее однозначно восстановить. Расположим эти элементы в определенном порядке. Каждый такой элемент будет представлять собой дискретную случайную величину. Будем рассматривать эти элементы последовательно. В начале сопоставим всей последовательности интервал [0; 1).
Пусть на некотором шаге обрабатывается элемент с номером i и текущий интервал равен [ai-1; bi-1). Пусть i-й элемент
может принимать Ki значений (пусть это будут целые числа от 1 до K) и известны вероятности этих значений Pi1, Pi2, ..., PiK.
Каждому возможному значению j i-го элемента соответствует некоторый интервал [cij; dij), причем ci1=ai-1,
diK=bi-1, cij=di,j-1 (2≤j≤Ki), т.е. интервалы всех возможных значений не
пересекаются и полностью покрывают текущий интервал [ai-1; bi-1). Пусть ширина каждого интервала будет прямо пропорциональна
вероятности соответствующего значения. Тогда для всех j от 2 до Ki можно записать 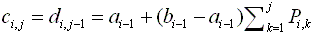 .
Если в данной последовательности значение текущего элемента равно v, то интервал [ai-1; bi-1) заменяется интервалом
[ai; bi)=[civ; div). После сужения интервала для текущего элемента происходит переход к следующему
элементу, и.т.д.
.
Если в данной последовательности значение текущего элемента равно v, то интервал [ai-1; bi-1) заменяется интервалом
[ai; bi)=[civ; div). После сужения интервала для текущего элемента происходит переход к следующему
элементу, и.т.д.
После обработки всех элементов сжимаемой последовательности для ее однозначного восстановления необходимо знать любое из вещественных чисел, лежащих в полученном интервале [a; b) и ожидаемую структуру последовательности (т.е. количество ее элементов, возможные значения каждого элемента и вероятности этих значений).
Рассмотрим процесс восстановления элементов исходной последовательности по некоторому числу из интервала [a; b). В начале текущий интервал положим равным [0; 1). Любое входное число попадает в этот интервал.
Пусть на некотором шаге текущий интервал равен [ai-1; bi-1), а текущий рассматриваемый элемент с номером i может принимать Ki значений с вероятностями Pi1, Pi2, ..., PiK, каждому из которых соответствует интервал [cij; dij). Пусть входное число лежит в интервале [ai-1; bi-1). Поскольку все интервалы [cij; dij) (1≤j≤K) не пересекаются и полностью покрывают интервал [ai-1; bi-1), то входное число принадлежит ровно одному из них. Если это интервал [civ; div), то он становится текущим интервалом [ai; bi) (при этом входное число по-прежнему лежит в текущем интервале), а v становится значением текущего рассматриваемого элемента i. После этого рассматривается следующий элемент, и.т.д. После нахождения всех элементов по ним строится исходная последовательность.
Как следует из процедуры кодирования и декодирования, интервальное кодирование является обратимым процессом, при котором не происходит потерь информации. При этом вероятности значений, используемые при кодировании и декодировании обязательно должны совпадать.
Если при кодировании неизвестны законы распределения отдельных элементов последовательности, то используются их приближенные оценки. Чем ближе эти оценки к истинным законам распределений, тем ближе размер сжатой последовательности, выраженный в битах, к величине информационной энтропии этой последовательности. Из этого следует, что эффективность сжатия напрямую зависит от точности используемых оценок законов распределения ее элементов.
В разработанном формате для предсказания законов распределения вероятностей значений элементов используется контекстное моделирование. Кодируемыми элементами являются элементы массивов, полученных при волновом преобразовании изображения.
Читать дальше: Контекстное моделирование| Биография |
ДонНТУ >
Портал магистров ДонНТУ |
| Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание | |