| Биография |
ДонНТУ >
Портал магистров ДонНТУ |
| Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание | |
Общие сведения о сжатии
Все данные в современных информационных системах могут быть представлены как последовательности бит определенной длины. Под сжатием без потерь можно понимать обратимое преобразование последовательности бит длиной N, хранящей данные в некотором формате, в последовательность бит длиной K (K<N).
Любое сжатие информации без потерь основано на использовании информационной избыточности данных. Разобьем данную последовательность бит на N подпоследовательностей. Пусть i-я подпоследовательность может принимать Ki значений с вероятностями Pij (1≤j≤Ki). Информационная избыточность проявляется в том, что для некоторых i, j и k Pij≤Pik при условии, что известны точные значения всех подпоследовательностей, кроме i-й. Если для любых допустимых i, j и k Pij=Pik, то последовательность не обладает информационной избыточностью и невозможно создать алгоритм, сжимающий последовательности такого вида.
Под контекстной зависимостью между подпоследовательности i от подпоследовательности k понимается зависимость между значениями Pij и конкретным значением подпоследовательности k.
Для численной оценки объема информации без учета избыточности используется величина информационной энтропии. Величина 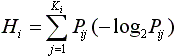 называется информационной энтропией
подпоследовательности i, а величина
называется информационной энтропией
подпоследовательности i, а величина 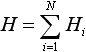 - информационной энтропией всей последовательности.
- информационной энтропией всей последовательности.
Математическое ожидание длины произвольной последовательности бит после сжатия идеальным алгоритмом, при условии, что априорно известны законы распределения вероятностей для всех ее подпоследовательностей, будет равно информационной энтропии этой последовательности. Для любых реальных алгоритмов сжатия математическое ожидание длины будет не меньше этого значения. Энтропия не зависти от конкретного разбиения данной последовательности на подпоследовательности. Алгоритмы сжатия, использующие в явном виде информацию о распределении вероятностей частей последовательности, называются алгоритмами энтропийного кодирования. Примеры таких алгоритмов - кодирование Хаффмана и арифметическое сжатие.
Все существующие алгоритмы сжатия используют некоторые априорные сведения об информационной избыточности сжимаемых данных. Например, архиваторы общего назначения используют то, что в файлах закон распределения вероятностей значений каждого байта зависит от соседних байт, или, что то же самое, некоторые последовательности байт встречаются чаще других. При сжатии данных определенных типов (изображения, видео, звук, результаты измерений некоторых величин определенным способом, и т.д.) используются знания о специфических видах информационной избыточности этих данных, что позволяет сжимать их эффективнее, чем при использовании универсальных алгоритмов.
Читать дальше: Классы изображений| Биография |
ДонНТУ >
Портал магистров ДонНТУ |
| Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание | |