В статье выполнено сравнение прогнозирующих свойств регрессионных моделей и моделей метода группового учета аргументов (МГУА) на примерах задач моделирования объема производства легкой промышленности и процесса инфляции. Приведен также способ выбора аргументов, наиболее существенных (информативных) для имеющейся выборки данных, позволяющий существенно уменьшить вычислительные затраты благодаря исключению неинформативных аргументов из процесса моделирования.

          Исходная таблица данных для моделирования объема производства легкой промышленности, взятая из [1], содержит 23 исходных аргумента (NA = 23): X1 - доходы населения (млрд. грн.), Х2 - индекс потребительских цен (% - 100), Х3 - индексы ВВП (% - 100), Х4 - объем производства промышленности, всего (млрд. грн.), Х5 - розничный товарооборот, всего (млрд. грн.), Х 6 - индексы зарплаты (реальная, % - 100), Х7- средние банковские процентные ставки на кредиты (% -100), Х8 - официальный курс гривны к доллару США (грн.), Х9 - налог на добавленную стоимость (млрд. грн.), Х10 - налог на прибыль предприятий (млрд. грн.), Х11 - расходы консолидированного бюджета , всего (млрд. грн.), Х12 - расходы бюджета на народное хозяйство (млрд. грн.), Х13 - индекс оптовых цен легкой промышленности (% - 100), Х14 - занятость в легкой промышленности (млн. человек), Х15 - общая занятость (млрд. человек), Х16 - заработная плата (номинальная, грн.), Х17 - учетная ставка для коммунальных банков (% - 100), Х18 - денежная масса наличности в обращении (млрд. грн.), Х19 - дебиторская задолженность (млрд. грн.), Х20 - кредиторская задолженность (млрд. грн.), Х21 - акцизный сбор (млн. грн.), Х22 - налог на доход граждан (млн. грн.), Х23 - доход консолидированного бюджета (млрд. грн.).

          При большом числе исходных аргументов построение модели занимает очень много машинного времени. В то же время практика построения моделей показывает, что среди представленных аргументов много несущественных, которые можно без ущерба для результирующей модели исключить. Ниже рассматривается один из способов решения этой проблемы. Следует отметить, что разделение аргументов на существенные и несущественные справедливо в основном для конкретного набора данных.

          В многорядном алгоритме МГУА к каждой i-й переменной оптимальным образом подбираются наилучший для данного случая ансамбль из остальных исходных аргументов [2]. Следовательно, можно построить структурную таблицу размером NA*NA, i-тая строка которой соответствует i-той модели, а j-тый столбец - j-тому аргументу (i,j=1 ,..., NA), значение ij-я ячейки этой таблицы равно j, если j-й аргумент участвует в формировании i-й модели , или 0, если не участвует. Эта таблица показывает, какие исходные аргументы участвуют в формировании каждой i-й модели. Определим значение "индекса полезности" j-го аргумента NumXj как число, показывающее, сколько раз данный исходный аргумент участвует в формировании всех моделей (частота использования j-го аргумента). Ясно, что эти числа лежат в интервале от 1 до NA. Если NumXj = 1, то можно утверждать, что j-й аргумент несуществен для данного случая, так как присутствует только в модели, где он включен насильно в соответствии со спецификой данного алгоритма отбора лучших моделей . Если NumXj = NA, то можно утверждать, что j-й аргумент существен для данного случая. Это крайние случаи, поэтому следует ввести некоторый порог для определения существенности j-го аргумента: будем считать аргумент существенным, если NumXj>0.5*NA. Кроме того, можно упорядочить аргументы по убыванию величины NumXj и, пользуясь дополнительными критериями, выбрать столько аргументов, сколько может быть допустимо в каждом конкретном случае.

          По многорядному алгоритму была получена следующая структурная таблица:

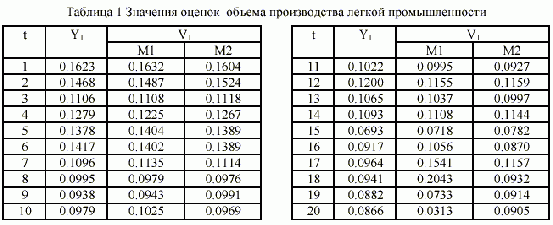
          Последняя строка таблицы показывает частоту участия каждого аргумента в формировании всех моделей . Если воспользоваться порогом NumXj>0.5*NA, получим, что для моделирования достаточен набор из следующих 13 аргументов: X1, X2, X4, X6, X7, X10, X11, X12, X13, X15, X16, X17, X19.

          Выходной величиной Y1 в данной задаче является объем производства легкой промышленности (млрд.грн.). В [1] приведены значения вышеперечисленных аргументов и выходной величины за период времени с ноября 1995 по июнь 1997 гг., т.е. длина исходной выборки - 20 точек. Отметим, что показатели Х1, Х2 и Х6 характеризуют уровень жизни населения, Х7, Х10-Х12 являются бюджетными, Х13 - отраслевой, Х17 - финансовый, а остальные являются макроэкономическими показателями.

          В рассматриваемом ниже примере в качестве экзамена, т.е. для проверки прогнозных свойств модели, оставим последние 5 точек. Это связано с тем, что для оценки 14 коэффициентов (13 аргументов и свободный член) по МНК и для вычисления их статистических оценок требуется по крайней мере 15 точек.

          Модель, полученная по МНК и включающая все тринадцать исходных аргументов, имеет вид (M1):

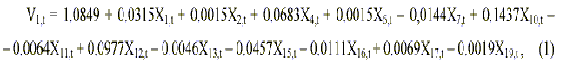
          где V1 - модельная оценка выходной переменной Y1, Xi,t - значение i-го аргумента в t-й точке (i = 1,2,3,4,6,7,10,11,12,13,15,16,17,19; t = 1 ,...,20).

          Модель имеет следующие характеристики:

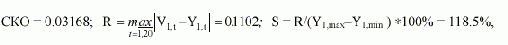
          где СКО - величина среднеквадратичного отклонения оценок Vt от табличных значений Y1,t, R - наибольшая абсолютная ошибка, S - относительная максимальная ошибка в процентах от наибольшего "размаха" значений Y1,t.

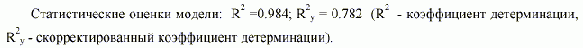
          Значения t-статистик ti : t0= 0.388; t1 = 0.631; t2 = 0.228, t4 = 1.948; t6 = 0.676; t7 = 0.681, t10= 0.502; t11 = 0.262, t12 = 0.784, t13 = 0.307, t15 = 0.339, t16= 0.666, t17= 0.657; t19 = 0.386. Табличное значение t(0.05,15) = 1.753.

          В таблице 1 приведены оценки объема производства легкой промышленности M1, полученные по модели (1), на рис.1 представлен график их изменения. Видно, что модель довольно плохая, причем наибольшие ошибки относятся к экзаменационным точкам. Несмотря на то, что только один коэффициент оказался значимым (t4 > 1.753), приравнять нулю остальные коэффициенты без дополнительных исследований нельзя [3]. Таким образом, МНК не позволяет построить модель, отражающую системные закономерности и пригодную для получения надежного прогноза, хотя по статистическим оценкам модель оказалась значимой.

          Модель по МГУА, построенная при тех же условиях, имеет вид (M2):

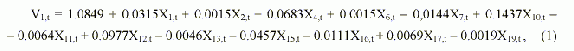
          Статистические оценки модели:

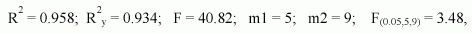
          где F,F(L,m1,m2) - расчетное и табличное значения критерия Фишера с уровнем значимости L и степенями свободы m1 и m2.

          Значения t-статистик ti (i = 0,2,4,6,10,13): t0 = 43.434, t2 = 5.899, t4= 6.132, t6 = 5.216, t10=3.573; t13 = 2.769. Табличное значение t(0.05,15) = 1.753.

          В таблице 1 приведены оценки объема производства легкой промышленности M2, полученные по модели (2), на рис.1 представлен график их изменения. Из приведенных данных видно, что модель МГУА значительно лучше МНК-модели как по прогнозирующим свойствам, так и в смысле значимости коэффициентов и всей модели в целом. При этом важно отметить, что модель МГУА значительно проще, т.е. включает меньше аргументов и, соответственно, меньше оцениваемых параметров.

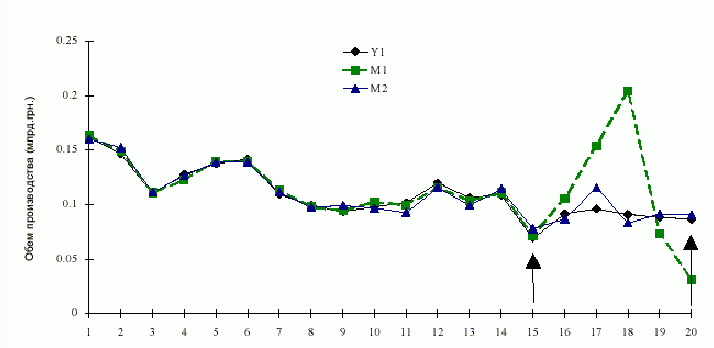
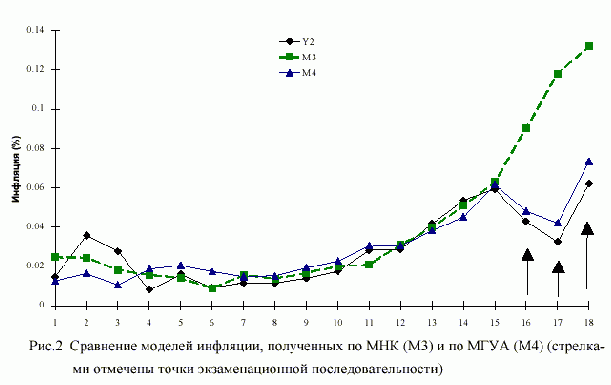
          Рис 1. Сравнение объема производства легкой промышленности, полученных по МНК (М1) и по МГУА (М2) (стрелками отмечены начало и конец экзаменационной последовательности

          Для построения модели по данным, взятым из [4], по описанному выше способу анализа структур моделей, построенных по многорядному алгоритму МГУА, были отобраны наиболее существенные аргументы. Ими оказались: Х1 - накопления личные ($ млн.); Х2 - число безработных всего; Х3 - процентные ставки (по Муди); Х4 - потребление личное ($ млн.); Х5 - доходы личные ($ млн.); Х6 - валовой национальный продукт. Выходной величиной является инфляция Y2 (рассчитывалась по формуле, приведенной в [4]). Соответствующие данные приведены в [5].

          По имеющейся выборке данных строились модели зависимости инфляции от текущих значений аргументов, причем три последние точки выборки составляли экзаменационную последовательность, т.е. для получения модели использовались только первые пятнадцать точек. Выбор такого варианта расчетов связан с резким изменением характера развития процесса. Ставилась задача: можно ли, используя данные, относящиеся к периоду монотонного развития инфляции, предсказать это резкое изменение? Другими словами, следовало проверить, заложено ли это изменение в предыстории и можно ли его выявить с помощью моделирования.

          Модель, полученная по МНК и включающая все шесть исходных аргументов, имеет вид:

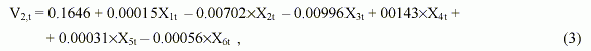
          где V2 - модельная оценка выходной переменной Y2, Xit - значение i-го аргумента в t-й точке (i = 1 ,...,6; t = 1 ,...,18).

          Модель имеет следующие характеристики качества:

          СКО = 0.0297; R = 0.0854 ; S =157.9%;

          и следующие статистические характеристики:

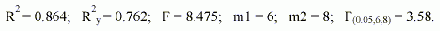
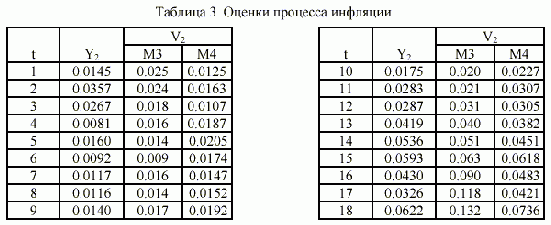
          Значения t-статистик ti (i = 0,1 ,..,6): t0 = 2.9155; t1 = 0.296; t2 = 1.619; t3 = 1.005; t4 = 0.685; t5 = 1.801; t6 = 2.927; t(0.05,15) = 1.753.

          В таблице 3 приведены оценки M3 инфляции (МНК), полученные по модели (3), на рис. 2 представлен график их изменения. Видно, что модель довольно плохая, причем наибольшие ошибки относятся к трем экзаменационным точкам, когда тенденция развития инфляции резко изменилась. Таким образом, МНК не позволяет построить модель, отражающую системные закономерности и пригодную для получения надежного прогноза, несмотря на то, что по статистическим оценкам она значима F > F(0.05,6,8), t0, t5, t6 > t(0.05,15).

          Модель инфляции, полученная при тех же условиях по МГУА (M4), имеет вид:

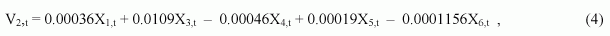
          характеризуется такими показателями качества:

          CKO = 0.00873; R = 0.0 1 94; S = 35.9%

          и имеет следующие статистические характеристики

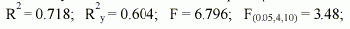
          Значения t-статистик ti (i = 1,3,4,5,6): t1 = 0.631; t3 = 1.252; t4 = 0.816; t5 = 1.299; t6 = 2.646. t(0.05,15) = 1.753.

          В таблице 3 приведены оценки M4 инфляции (МГУА), полученные по модели (4), качество этой модели наглядно характеризует также рис. 2. Видно, что она четко отражает изменение тенденции процесса, не очевидное из предыдущей информации, т.е. из предыстории (до 16-й точки) процесса.

          Важно отметить, что улучшение прогноза состоялось за счет у прощения прогнозирующей модели (в данном случае за счет исключения из нее аргумента Х2), что характерно именно для применения МГУА (эффект исключения "лишних", неинформативных факторов).

          1. Бюлетень економiчної кон'юнктури України. - Київ: НДI статистики Мiнстату України. - 1997. - випуск №3. - 134c.

          2. Справочник по типовым программам моделирования / Под ред. А.Г. Ивахненко. - К.: Технiка, 1980. - 184с.

          3. Вучков И., Бояджиева Л., Солаков Е. Прикладной линейный регрессионный анализ. - М.: Финансы и статистика, 1987. - 239 с.

          4. Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия: В 2-х вып. Вып. 2. - М.: Финансы и статистика, 1982. - 239с.

          5. Степашко В.С., Коппа Ю.В. Опыт применения системы АСТРИД для моделирования экономических процессов по статистическим данным // Кибернетика и выч. техника, 1999. - Вып . 117. - С. 23-29.

          Получено 11 .05.2000

Вверх