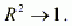| П.И. Бидюк, Т.Ф. Зворыгина |
Структурный анализ
|
|
Источник:
www.gmdh.net/articles/usim/Bidyuk.pdf |
|
В работе выполняется анализ методик построения моделей типа авторегрессии со скользящим средним (АРСС), АРСС с эндогенными переменными (АРССЭ) или АРСС с интегрированным скользящим средним (АРИСС) [1-4]. При этом указаны основные этапы моделирования временных рядов, рассмотрено понятие структуры модели и описаны варианты обычно применяемых методов и критериев на каждом из этапов. |
|
В соответствии с предлагаемым подходом построение модели по временным рядам состоит из следующих этапов:
Понятие структуры модели включает в себя:
Введение случайной составляющей в модель обуславливается следующими основными причинами: присутствие неконтролируемых внешних возмущений, введение в модель излишних или, наоборот, отсутствие в модели необходимых объясняющих переменных, влияние методических и вычислительных погрешностей. Выбор структуры модели, адекватной процессу, - задача весьма не простая и решается, как правило, итеративно или с применением некоторого метода регулярного перебора вариантов. Если ни одна из моделей-кандидатов не может считаться адекватной, то необходимо исследовать на информативность экспериментальные данные, которые могут быть недостаточно информативными для оценивания модели. В таком случае может потребоваться повторный или дополнительный сбор экспериментальных данных. |
|
АНАЛИЗ ПРОЦЕССА |
|
На этом этапе необходимо воспользоваться всей имеющейся информацией о процессе с целью: определения числа его входов и выходов; выяснения логических взаимосвязей между переменными; установления возможного присутствия нелинейностей и их характера; определения типа возмущений, действующих на процесс; определения присутствия запаздываний на качественном и, возможно, количественном уровнях; приблизительного определения порядка процесса. В случае исследования экономических процессов необходимо установить, имеется ли влияние сезонных эффектов, присутствует ли тренд (на качественном уровне); возможно, возникнет необходимость выдвинуть гипотезу о существовании случайного тренда; если участки временных рядов с существенно различающимися уровнями колебаний (присутствие гетероскедастичности); оценить необходимость использования гипотезы о коинтегрированности переменных. В результате анализа процесса необходимо в общем виде постулировать структуру математической модели, которая будет использоваться в дальнейшем для описания его поведения. Например, если выдвигается гипотеза о существовании гетероскедастичности, то необходимо выбрать возможный класс моделей для ее описания. То же самое касается присутствия коинтегрированности переменных или случайного тренда. |
|
ОПРЕДЕЛЕНИЕ НАЛИЧИЯ НЕЛИНЕЙНОСТЕЙ |
|
Для решения этой задачи можно пользоваться различными критериями. Однако при этом необходимо знать об их возможностях. При построении регрессионных моделей можно воспользоваться простыми тестами, например, статистикой [5]. |
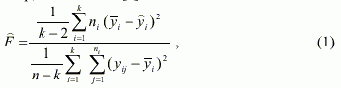
|
|
где k - число групп данных; ni - число измерений в группе; n - общее число измерений. Фактически эта статистика представляет собой отношение отклонений средних значений от прямой регрессии к отклонениям значений y(k) от групповых средних. Если статистика F с v1=k-2, v2=n-k степенями свободы превосходит уровень значимости, то гипотезу о линейности нужно отбросить. При этом нужно помнить, что этой статистикой можно обоснованно пользоваться лишь в случае, когда структура модели задана. Если же существуют несколько возможных структур, то возникнут сложности, связанные с тем, что в статистику входят оценки yi. |
|
ВЫБОР КЛАССА СТРУКТУР МОДЕЛЕЙ-КАНДИДАТОВ |
|
Коэффициент корреляции, а в общем случае корреляционная функция, позволяют установить наличие связи между эндогенными (зависимыми) и экзогенными (независимыми) переменными. Корреляция может быть линейная или нелинейная в зависимости от типа зависимости, фактически существующей между переменными. В большинстве практических случаев рассматривают линейную корреляцию (взаимосвязь), однако более глубокий анализ требует привлечения для исследования процессов нелинейных зависимостей. Сложную нелинейную зависимость можно упростить, но знать о ее существовании необходимо для того, чтобы построить адекватную модель процесса. Коэффициенты корреляции показывают степень взаимосвязи между переменными. Очевидно, что, прежде чем формально вычислять коэффициенты корреляции, необходимо выполнить анализ процесса и определить присутствие (или отсутствие) логической связи между переменными. Это позволяет ввести в рассмотрение только те переменные, которые действительно влияют на зависимую. Очевидно, что для правильного выбора переменных необходимо достаточно глубоко знать моделируемый процесс (для решения этой задачи введен первый этап). Для определения необходимости включения в уравнение регрессии авторегрессионной составляющей следует вычислить и исследовать выборочную автокорреляционную и частную автокорреляционную функцию переменной y(k). Уравнение с авторегрессионной составляющей имеет вид: |
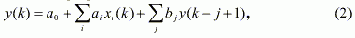
|
|
то есть в уравнении регрессии добавлена авторегрессионная (АР) составляющая. Порядок авторегрессии определяется с помощью автокорреляционной функции. Число коэффициентов автокорреляционной функции, которые отличны от нуля в статистическом смысле, и будет составлять порядок авторегрессии. Коэффициенты автокорреляционной функции вычисляются по формуле: |
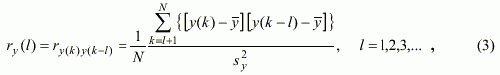
|
|
где
Уточнить порядок авторегрессионной составляюшей позволяет частная автокорреляционная функция (ЧАКФ), которая вычисляется в соответствии с выражениями: |
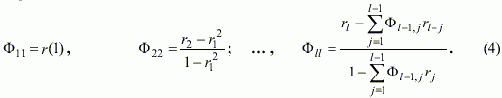
|
|
ЧАКФ четче отражает порядок корреляции АР-модели благодаря отсутствию влияния промежуточных коэффициентов корреляции на выбранные значения переменной, то есть, коэффициент Ф11 характеризует степень взаимосвязи между стоящими рядом (по времени) значениями переменной, а Ф22 характеризует взаимосвязь между значениями переменной, отстоящими на расстоянии двух периодов дискретизации. Когда говорят, что значения коэффициентов автокорреляционной функции должны быть отличными от нуля в статистическом смысле, это означает, что существует некоторое выражение, которое позволяет подтвердить или опровергнуть этот факт. Одним из общепринятых подходов к определению того, что коэффициенты АКФ существенно отличны от нуля в статистическом смысле, есть вычисление статистического параметра (статистики) Льюнга-Бокса Q(Rk) по формуле [2,4]: |
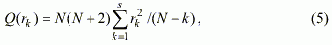
|
|
где N - длина выборки данных переменной, для которой найдены значения автокорреляционной функции Rk; s - число коэффициентов АКФ, которые исследуются на существенное отличие от нуля. Более сложные процедуры выбора множества классов моделей описаны в [6]. |
|
ВЫБОР СПОСОБА ГЕНЕРАЦИИ СТРУКТУР МОДЕЛЕЙ |
|
После определения порядка АР-модели можно воспользоваться генеретором структур моделей различной сложности с применением некоторого метода регулярного перебора вариантов при заданном числе запаздываний. Для выбора наиболее подходящего генератора структур необходимо учесть такие факторы, как количество входных переменных, ограничения на время решения и уроень требований к модели. Заметим, что при ограниченном времени и простой модели применяются методы включения и исключения, при необходимости получить более достоверную модель - метод включения-исключения [7], а в случае большого количества переменных применяются методы ветвей и границ, а также различные методы из семейства МГУА [8] комбинаторно-селекционный, линейный или нелинейный многорядный МГУА. |
|
ВЫБОР КРИТЕРИЯ СЕЛЕКЦИИ МОДЕЛЕЙ |
|
На этом этапе выбирают лучшую линейную или псевдолинейную (линейную по коэффициентам) модель из множества моделей-претендентов. Критерий селекции моделей зависит от типа возмущений, влияющих на процесс, и целей, которые преследуются при моделировании. При вычислении критериев часто используется остаточная сумма квадратов ошибок модели: |
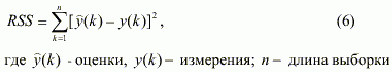
|
|
Сама эта величина не может служить критерием для выбора структуры, поскольку пр увеличении сложности модели s происходит все более точное приближение к входным данным, что допустимо только при отсутствии возмущений. Если известно, что шум распределен по нормальному закону, то применяются следующие критерии: Скорректированный RSS: RSS/(n-s) Статистика Фишера: |

|
|
Если возможно получить оценкудисперсии шума, применяется критерий Маллоуза: |

|
|
Единственный критерий, который применим при любом известном распределении шума - это информационный критерий Акаике (AIC): |

|
|
Этот критерий существенно ограничивает рост сложности модели наличием аддитивного члена 2s. Однако проблема применения состоит в том, что в практических задачах функция распределения шума неизвестна. В частном случае нормального шума он принимает вид критерия Маллоуза. При этом на практике он применяется в виде |

|
|
В последнее время эта формула называется критерием Акаике-Маллоуза [9]. Популярным является критерий, называемый финальная ошибка прогнозирования, который не требует дополнительной информации и вычисляется так: |

|
|
КРИТЕРИЙ С РАЗБИЕНИЕМ ВЫБОРКИ |
|
Если статистические оценки данных не известны, то применяются внешние критерии с разбиением выборки ("перекрестного обоснования") [8].
Здесь рассмотрим разбиение на три непересекающихся подвыборки
(подмножества точек) А,В,С, причем обозначим также
|
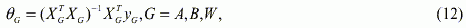
|
|
а значение ошибки на некоторой подвыборке Q по модели, оценки параметров которой вычислены на G, равно |

|
|
где Q=A,B,W,C. Разбиение на три подвыборки соответствует следующему: |
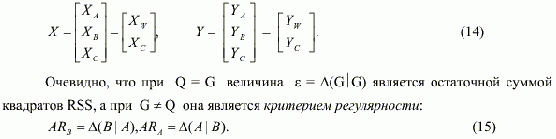
|
|
Тогда критерий симметричной регулярности имеет вид: |

|
|
Критерий непротиворечивости (несмещенности) определяется выражением: |
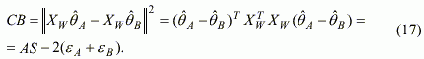
|
|
Широко известен критерий Кейна, применяемы только тогда, когда известно, что шум нормальный: |
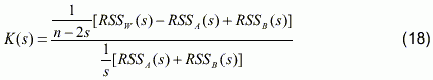
|
|
Существует еще один популярный критерий, называемый критерий "скользящего контроля", "усредненный критерий регулярности", или "джекнайф": |
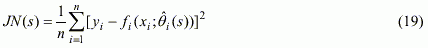
|
|
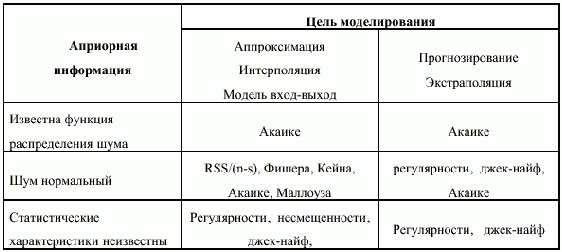
Простого перечня врзможных критериев не достаточно, так как каждому исследователю, не являющемуся экспертом в области моделирования, на практике нужно решать задачу выбора наиболее подходящего критерия из списка возможных. Для решения этой задачи необходимо провести анализ применимости (ограничений на применение) различных критериев. Примером методики такого анализа может служить следующая таблица. |
|
|
Содержание данной конкретной таблицы не претендует на полноту и однозначность, поскольку ее заполнение зависит от мнений различных экспертов в области моделирования, обладающих своими привычками, опытом и предпочтениями. Однако составление такого рода таблиц необходимо, так как является одним из основных этапов разработки правил принятия решения в области моделирования по данным наблюдений [11]. Если говорить конкретно о критериях селекции моделей, то следующим шагом процесса выбора должен стать анализ их применимости в зависимости от количества данных, по которым строится модель. Некоторые критерии не могут работать с малым количеством данных, в то время как при достаточном их количестве может не врзникнуть необходимости применять сложные критерии, можно обойтись более простыми. |
|
ОЦЕНИВАНИЕ КОЭФФИЦИЕНТОВ МОДЕЛЕЙ-КАНДИДАТОВ |
|
На этом этапе вычисляют оценки коэффициентов моделей-кандидатов, которые различаются своей структурой. Например, моделью-претендентом может быть авторегрессионная составляющая первого, второго и третьего порядка. Могут проверяться модели, включающие по отдельности объясняющие переменные, а также модели, которые содержат все объясняющие переменные вместе. Наиболее распространенными методами оценивания параметров модели являются следующие: метод наименьших квадратов (МНК) и его модификации; метод максимального правдоподобия (ММП); метод вспомагательной переменной (МВП); нелинейный метод наименьших квадратов (НМНК) и их рекурсивные версии. Все эти методы имеют свои условия применения. Например, для получения несмещенных оценок вектора параметров регрессионной модели с помощью метода наименьших квадратов необходимо проверить выполнение известных предположений классического регрессионного анализа [7]. |
|
ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ |
|
На этом этапе оценивают степень адекватности модели природе процесса в целом и имеющимся априорным предположениям. В принципе значения упомянутых выше критериев, применяемых для селекции моделей, являются также некоторыми характеристиками адекватности модели. Однако на практике принято использовать дополнительные оценки адекватности, такие как: t-статистика Стьюдента. Значимость каждого из коэффициентов регрессии в статистическом смысле определяют с помощью t - статистики,которая вычисляется по формуле [7]: |
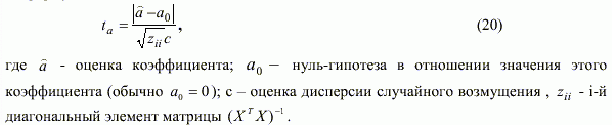
|
|
Для определения значимости коэффициента необходимо учитывать длину выборки N, число оцениваемых параметров p и задаться уровнем значимости. Уровень значимости указывает долю ошибочно принятых решений о значимости параметров при оценивании регрессии. Если вычисленное значение по сравнению с табличным tкрит удовлетворяет условию |

|
|
то нуль-гипотеза о не значимости коэффициента принимается; в противном случае она отвергается и коэффициент считается значимым. Чем больше будет значение ta, тем более высокой будет значимость конкретного коэффициента.
Коэффициент детерминации
В качестве меры информативности временного ряда часто
используют его дисперсию. Коэффициент
|
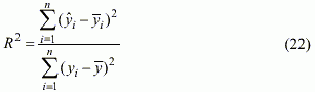
|
|
Очевидно, что для адекватной модели коэффициент детерминации должен
стремиться к единице, то есть:
Критерий Байеса-Шварца (BSC). Данный критерий похож на критерий Акаике (9), однако он учитывает дополнительно длину выборки с помощью члена ln(N): |

|
|
Его используют при длинных выборках измерительных данных. Статистика Дарбина-Уотсона (Durbin-Watson) Статистика Дарбина-Уотсона вычисляется по формуле: |

|
|
где p - коэффициент корреляции между значениями случайной переменной, т.е. p=cov[e(k)]=E[e(k)e(k-1)]. Этот параметр позволяет определить степень коррелированности ошибок модели. При полном отсутствии корреляции между ошибками DW=2, то есть это наиболее приемлемое значение данного параметра. На этом этапе также можно применять более сложные критерии, такие как критерий Уиттла, Хеннана, Бартлетта и тест на сериальную независимость [4]. В последние годы важнейшей дополнительной характеристикой адекватности модели считается ее проверка на дополнительной части выборки, которая не использовалась при составлении модели [2,12]. Необходимость такого разделения выборки данных обусловлена тем, что модель с наибольшим количеством переменных, как правило, не дает лучшее качество прогноза, чем модель с оптимальным количеством переменных, хотя последняя имеет худшие аппроксимирующие свойства. Отметим, что этот критерий (в виде проверки на третьей, экзаменационной части выборки данных) используется в алгоритмах МГУА с момента его зарождения, однако широкое распространение он приобрел лишь в последние годы [2]. |
|
ЗАКЛЮЧЕНИЕ |
|
Рассмотренные в обзоре методы и критерии, использующиеся при моделировании по данным наблюдений, далеко не исчерпывают то множество способов, которое практически используется исследователями. Эта работа содержит общий анализ основных этапов процесса решения задачи моделирования и описание множеств решений на каждом из них. Следующим шагом работы должен стать анализ прикладных задач. Его можно провести как путем анализа литературы и изучения мнений экспертов, так и путем вычислительных экспериментов. Типовые задачи определяются объемом и характером априорной информации об объекте и неопределенностях. Пример такого анализа дан в работе в виде таблицы применения критериев селекции моделей. |
|
ЛИТЕРАТУРА |
|
1. Бокс Дж., Дженкинс Г. Анализ временных рядов (т. 1,2). - М.:1974.-406с. 2. Кашьяп Р.Л., Рао А.Р. Построение динамических стохастических моделей по экспериментальным данным/ Пер. с англ. - М.: Наука, 1983.- 384с. 3. Конева Е.С. Выбор моделей для реальных временных рядов // Автоматика и телемеханика, №6, 1988, стр. 3-18. 4. Enders W. Applied econometric time series. - New York: Wiley $ Sons, 1994. - 433p. 5. Закс Б. Статистическое оценивание. - М.:Статистика, 1976. - 598 с. 6. Бідюк П.І., Половцев О.В. Аналіз та моделювання економічних процесів перехідного періоду. - Київ:ПЛАБ - 75, 1999.- 230с. 7. Вучков И., Бояджиева Л., Солаков Е. Прикладной регрессионный анализ / Пенр. с болг. - М.: Финансы и статистика, 1987. - 239с. 8. Ивахненко А.Г., Степашко В.С. Помехоустойчивость моделирования. - Киев.: Наукова Думка, 1984. - 295 с. 9. Стадник М.П. Модификация критерия Мэллоуза-Акаике для подбора порядка регрессионной модели / Автоматика и телемеханика. - 1988. - №4. - С. 98-108. 10. Степашко В.С. Алгоритмы МГУА как основа автоматизации процесса моделирования по экспериментальным данным. // Автоматика. - 1988. - №4. - С. 44-45. 11. Степашко В.С., Зворыгина Т.Ф. О проектировании диалоговой оболочки СППР для моделирования по данным наблюдений. // Модлелирование и управление состоянием эколого-экономических систем региона. - Киев, 2001. - С. 64-69. 12. Енюков И.С. Методы, алгоритмы программы многомерного статистического анализа и пакет ППСА. - Москва, Финансы и статистика, 1986. - 232 с. |
|
Бидюк П.И., Зворыгина Т.Ф. |
|
СТРУКТУРНЫЙ АНАЛИЗ МЕТОДИК ПОСТРОЕНИЯ РЕГРЕССИОННЫХ МОДЕЛЕЙ ПО ВРЕМЕННЫМ РЯДАМ НАБЛЮДЕНИЙ |
|
Задача построения авторегрессионных моделей по временным рядам наблюдений рассматривается как последовательность этапов анализа данных. Приведено краткое описание множеств возможных процедур на каждом из таких этапов с рекомендациями и ограничениями на их применение. Для одного из этапов - выбора критерия селекции моделей - приведен пример анализа применимости. |
|
Бідюк П.И., Зворигіна Т.Ф. |
|
СТРУКТУРНИЙ АНАЛІЗ МЕТОДИК ПОБУДОВИ РЕГРЕСІЙНИХ МОДЕЛЕЙ ЗА ЧАСОВИМИ РЯДАМИ СПОСТЕРЕЖЕНЬ |
|
Задача побудови авторегресійних моделей за часовими рядами спостережень розглядається як послідовність етапів аналізу даних. Наведено короткий опис множин можливих процедур на кажному з таких етапів з рекомендаціями й обмеженнями на їх застосування. Для одного з этапів - вибору критерію селекції моделей - наведено приклад аналізу застосовності. |
|
Bidiuk P.I., Zvorygina T.F. |
|
STRUCTURAL ANALYSIS OF METHODS OF REGRESSION MODEL CONSTRUCTION AFTER TIME SERIES OF OBSERVATIONS |
|
A problem of construction of auto regression models after the observed time series is investigated as a sequence of stages of data analysis. Short description of sets of possible procedures for each stage is provided with suggestions and restrictions concerning its application. Applicability analysis is given for the stage of definition of a model selection criterion. |
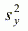 - выборочная дисперсия переменной y(k). Число коэффициентов АКФ,
отличных от нуля в статистическом смысле, указывает на
порядок авторегрессионной части модели.
- выборочная дисперсия переменной y(k). Число коэффициентов АКФ,
отличных от нуля в статистическом смысле, указывает на
порядок авторегрессионной части модели.
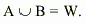 Для стандартизации записи формул примем следующие обозначения:
оценка параметров по МНК на некоторой подвыборке G равна
Для стандартизации записи формул примем следующие обозначения:
оценка параметров по МНК на некоторой подвыборке G равна