| R. Cotcher, F.Chance |
Capacity Planning in the Face of Product-Mix Uncertainty |
|
Èñòî÷íèê:
www.fabtime.com/files/ISSM99.pdf |
|
This paper describes a straightforward method of quantifying the sensitivity of production capacity to product mix. In capacity planning over horizons with unpredictable product mix, this methodology quantifies the risk of underinvestment in capacity. Actions that can be taken to prevent mix-driven capacity shortfalls are described. The implementation of this methodology at Headway Technologies is also presented. |
|
INTRODUCTION |
|
In capacity planning for wafer fabrication facilities, the need for additional production equipment must be identified and the equipment ordered far in advance of its actual use. If product mix is highly predictable, or if all products use each piece of production equipment equally, an overall production forecast is all that is needed to determine equipment requirements. But when a wafer of one product loads a tool to a greater degree than does a wafer of another product, any deviation from the expected product mix could leave the facility with insufficient capacity, even if total production volume is right on forecast. To demonstrate, let's look at a simple case of a single-tool factory, with no downtime or rework. Product A requires 1 hour per wafer on the tool; Product B requires 2 hours per wafer. With a 50/50 mix and a total of 16 wafers per day, total required production time is (8)(1) + (8)(2) = 24 hours-so we have just enough capacity. But if product mix shifts to 25% Product A and 75% Product B, total required production time is (4)(1) + (12)(2) = 28 hours, and we have insufficient capacity, even though total production volume has remained unchanged. Expand this example to include a dozen or more constantly changing products and hundreds of tools, and we have the real world…and a threat to capacity that is immensely complicated to answer. This is a concern for Headway Technologies, a manufacturer of leading-edge read-write heads. A read-write head is a tiny integrated circuit, about the size of a grain of pepper, that magnetically reads and writes data onto and off of a disk in a disk drive. Heads are manufactured in the form of wafers, each consisting of 15,000-20,000 identical heads, each containing many layers of microscopic circuitry. Each wafer makes 300 to 400 visits to different process equipment during its manufacture. At any time, Headway has ten to twenty products in production, each with its own unique process flow. Each product is typically produced for only a few months before being replaced by a new, advanced version. New products typically start out as low-volume R&D projects but sometimes ramp quickly into mass production when they are qualified and approved by a customer. In this environment, although total production volume can be forecast with some degree of accuracy, the mix of individual products is difficult to predict, along with its effect on the company's capital-equipment needs. Headway's longest-lead-time capital equipment must be ordered approximately one year in advance of need. The company therefore uses a one-year planning horizon for capital-equipment purchases. The key tool employed in purchase decisions is a fab capacity and simulation model created using Wright Williams & Kelly's Factory Explorer® software. |
|
METHOD FOR QUANTIFYING THE SENSITIVITY OF PRODUCTION CAPACITY TO PRODUCT MIX |
|
It should be noted that the following technique works only in situations in which the tools do not have setups (a setup is a routine reconfiguration required to enable a tool to perform different classes of operations) or unit-based downtimes. This paper's methodology remains valid in either situation, but setups and unit-based downtimes cause the relationship between wafers processed and tool capacity loading to become non-linear. In such situations, multiple model runs could be used to zero in on the answers. That more complicated technique we leave to another paper, though the groundwork is laid here. Step 1. Determining Tool Sensitivity to Product Mix Headway starts its product-mix sensitivity analysis by putting into its model all the production equipment that it plans to have in place one year in the future. This equipment is optimum for the company's forecast product mix, but Headway needs to see what tools it would require to accommodate other possible product mixes. Headway runs the capacity model with all products that might be in production one year from now. Since few if any of today's products can be expected to be in production at that time in their present forms, accommodation is made, as follows: (1) today's products that are expected to be the most enduring are put in the model as-is as a best representation of what each product will be like one year in the future; (2) variants of today's products are put in the model, each containing experimental design features that may become standard in the future; (3) today's R&D products are put in the model verbatim, as a best guess as to what the production wafer of the future will be like. Headway runs the model at the forecast total production volume for the period in question, consisting of all the above products in equal amounts, for reasons explained below. For example, if the forecast production volume one year from now is 1000 WGR ("weekly going rate"; = good wafers out per week), and the model consists of ten products, then the model is run at 1000 WGR, with a product mix of 100 WGR for each product. After the run, the capacity software is used to generate a worksheet showing the percentage of each tool group's utilized production capacity required for each product (a tool group is a set of interchangeable tools). Since the model is run with equal numbers of all products, tool groups that are loaded equally per product will see identical loading (10% per product in the above example). Figure A shows a portion of this worksheet for a simplified sample case involving three products at 300 WGR total volume. |
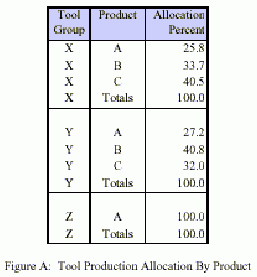
|
|
Any tool group that is loaded greater or less than average (Allocation Percent of 33.3% in the above example) by any product is mix sensitive. In Figure A, all three tool groups shown are mix sensitive. For example, for Tool Group Y, 100 wafers per week of Product A requires less of the tool group's production capacity than does 100 wafers per week of Product B (27.2% versus 40.8%). Tool Group Z is used by only one product. Step 2. Identifying Mix-Sensitive Tool Groups that May Become Capacity Constraints The capacity model is then run once for each product, with each run's production volume consisting 100% of a different product in the model. For each run, the capacity software generates a capacity loading estimate for each tool group. Capacity loading is defined as the actual throughput of the tool group divided by the maximum possible throughput of the tool group (after subtracting downtime). Any tool group loaded more than 85% in any run is noted as a potential capacity constraint. Though a tool loaded less than 100% is technically not a constraint, companies typically plan to buy an additional tool if any tool is projected to be loaded beyond 85%. This is because there is a correlation between capacity loading and cycle time, and loading a tool too close to 100% usually incurs a big cycle-time penalty. Buying sufficient tools to keep capacity loading below 85% is thus an indirect way of limiting cycle time. Defining "capacity" as a plant's output at some fixed loading below 100% is sometimes referred to as "cycle-time- constrained capacity" [1]. Though 85% is a commonly used level for this, Grewal et. al. [3] have developed a method for modifying the 85% rule on a tool-by-tool basis based on cycle time analyses of individual tools. For simplicity, however, 85% is used across the board in this paper. That said, all tool groups that the capacity software shows are never loaded beyond 85% can be ignored for the remainder of this analysis-they have proven themselves not to be capacity constraints even when the fab is dedicated to the product that loads them most heavily. The remaining tool groups are mix-driven capacity constraints- tool groups that could become capacity constraints if product mix shifts certain ways. The question is, to what extent do these tool groups pose a risk of constraining capacity? With multiple products loading each tool group at varying rates, the range of possible product mixes that could overload a tool is overwhelming. This is what makes difficult the question: "How can additional tool purchases be used to reduce the risk of mix-driven capacity shortfall?" This question is answered below. Step 3. Quantifying the Sensitivity of Production Capacity to Product Mix For each tool group that survived the above screening and remains as a mix-driven capacity constraint, capacity loading per wafer is calculated for the tool group's heaviest- and lightest-loading products. This is accomplished as follows:
Step 4. Identifying Tool-Purchase Points The above analysis tells us the rate at which a shift in product mix increases a tool group's capacity loading. But at what point will a shift in mix load the tool group to the point at which it will become a fab capacity constraint, necessitating the purchase of another tool? This question is answered using the following procedure:
Step 5. Quantifying and Prioritizing Mix-Driven Capacity Constraints In order to quantify the risk of under-investment in capacity, Headway puts the results of all of the calculations made thus far into a table as shown in Figure B. This table shows each tool group that is a mix-driven capacity constraint and the shift in volume that must occur between two products before that tool group actually constrains capacity. These volume shifts can be expressed in wafers, % of total production volume, or percent of either of the two products' volumes. Rows in the table can then be sorted by any of these attributes, with the lowest values at the top. The uppermost tool groups, then, are those that, with the smallest shift in product mix, will become capacity constraints. |
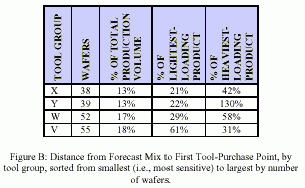
|
|
DISCUSSION |
|
Although Figure B shows product mixes that will cause capacity shortfalls, this list is by no means all-inclusive. This is because, given the number of products in the model, with each product loading each tool group to a different degree per wafer, the combination of product mixes that can cause a capacity shortfall is overwhelming. By making the assumption that, for each tool group, unfavorable product-mix changes only occur through the transfer of wafers from the lightest-loading product to the heaviest loading product, we have simplified this issue to the point where it can be quantified so that risks can be compared. Estimating Probabilities Now that we have identified tool-purchase points-those mixes that prompt the purchase of additional tools-we could divide all possible product mixes into constant-tool-set regions; i.e., regions over which a given tool set would be adequate (no tool loaded more than 85%). If one could then estimate the probability of the product mix ending up in each particular region, one could estimate the probability of having adequate capacity. Then one could trade off risk vs. tool purchase cost. This calculation is not difficult in a two-product case, but when many products are in the mix, the task becomes quite challenging. This paper's technique, with its simplifying assumptions, provides a straightforward method for assisting the largely intuitive decision of how to accommodate product-mix uncertainty. If a similarly simple method could be developed of dividing the universe of possible product mixes into constant-tool-set regions and assigning probabilities to these regions, this method's power would be augmented significantly. |
|
SUMMARY: ACTING ON THE FINDINGS OF THIS METHOD |
|
A major benefit of this method is that it tells one what tools not to worry about in regard to mix-driven capacity constraints. Headway has found that this method weeds out about 95% of its tool groups, leaving a manageable 5% as mix-driven capacity constraints. These tool groups then are the only ones that need be kept in mind when looking at signs of product-mix change and how they will affect fab capacity. Large fabs can expect a larger percentage of their tool groups to qualify as mix-driven capacity constraints. This is because large fabs have more of each type of tool and can therefore purchase capacity in smaller increments and have more tool groups close to 85% loading at any one time [4]. In such cases, analysis can be simplified by limiting consideration to those tool groups nearest the top of the Distance from Forecast Mix to First Tool-Purchase Point table (Figure B). However one comes to a list of possible mix-driven capacity constraints, the final question is, what specifically should be done with this information? Here are some possible courses of action:
In ways such as these, this method allows Headway to take the first step beyond traditional capacity planning. Where capacity planning answers the question "What capital equipment should Headway purchase to meet forecast?," this method answers the question "What capital equipment is likely to constrain the factory if actual product mix varies from forecast?" In the high-technology world of read-write heads, this method helps Headway to maximize, relative to cost, the probability of having adequate capacity for future demand. |
|
REFERENCES |
|
[1] J.W. Fowler and J.K. Robinson, 1995, “Measurement and Improvement of Manufacturing Capacity (MIMAC) Designed Experiment Report,” SEMATECH Technology Transfer #95062860A-TR. [2] F. Chance. Factory Explorer® Version 2.6 User Manual. [3] N. S. Grewal, A. C. Bruska, T. M. Wulf, and J. K. Robinson, 1998. “Integrating Targeted Cycle-Time Reduction Into the Capital Planning Process,” In Proceedings of the 1998 Winter Simulation Conference,ed. D. J. Medeiros, E. F. Watson, J. S. Carson, and M. S. Manivannan, 1005-1010. [4] E. Neacy, S.Brown, M. McDavid, J. Robinson, S. Srodes, T. Stanley, 1993, “Cost Analysis for a Multiple Product/Multiple Process Factory: Application of SEMATECH’s Future Factory Design Methodology,” Proceedings of the Advanced Semiconductor Manufacturing Conference, Boston, MA. |
|
AUTHOR BIOGRAPHIES |
|
Robert C. Kotcher received his B.S. degree in Industrial & Systems Engineering from San Jose State University, San Jose, California, in 1983, and his MBA degree from Santa Clara University, Santa Clara, California, in 1999. He is currently an industrial engineer for Headway Technologies, specializing in capacity planning and fab simulation. Dr. Frank Chance is a recognized expert in the modeling and simulation of complex manufacturing facilities. He is the author of Factory Explorer®, an integrated capacity, cost, and simulation analysis tool. He is a co-founder and principal of FabTime Inc. His clients in the semiconductor industry have included Seagate, Siemens, Headway, and IBM. Dr. Chance holds MS and Ph.D. degrees in Operations Research from Cornell University. He has taught at Cornell University and was a visiting assistant professor at the University of California, Berkeley, prior to founding Chance & Robinson. |
|
ACKNOWLEDGEMENTS |
|
The authors would like to thank Jennifer Robinson of FabTime Inc. and Steven Brown of Infineon for their contributions. |
|
|