КЛАССИЧЕСКАЯ ТЕОРИЯ КОМПИЛЯТОРОВ
ОГЛАВЛЕНИЕ
ЛОГИЧЕСКАЯ СТРУКТУРА КОМПИЛЯТОРА.. 6
ОСНОВНЫЕ ЧАСТИ КОМПИЛЯТОРА.. 8
Синтаксический и семантический анализ. 11
ТЕОРИЯ ФОРМАЛЬНЫХ ЯЗЫКОВ. ГРАММАТИКИ.. 14
ДЕТЕРМИНИРОВАННЫЕ И НЕДЕТЕРМИНИРОВАННЫЕ КОНЕЧНЫЕ АВТОМАТЫ 20
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ. ХЕШ-ФУНКЦИИ.. 29
СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ КОЛЛИЗИИ. РЕХЕШИРОВАНИЕ. 30
КОНТЕКСТНО-СВОБОДНЫЕ ГРАММАТИКИ.. 33
СИНТАКСИЧЕСКИ УПРАВЛЯЕМЫЙ ПЕРЕВОД.. 37
АВТОМАТЫ С МАГАЗИННОЙ ПАМЯТЬЮ... 41
ОПЕРАТОРНЫЕ ГРАММАТИКИ (ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВИЯ) 44
ВНУТРЕННИЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ ПРОГРАММЫ.. 52
ПРИЛОЖЕНИЕ. ВВЕДЕНИЕ В ПРОЛОГ. 67
В настоящем пособии излагаются основы классической теории компиляторов - одной из важнейших составных частей системного программного обеспечения.
Несмотря на более чем полувековую историю вычислительной техники, формально годом рождения теории компиляторов можно считать 1957, когда появился первый компилятор языка Фортран, созданный Бэкусом и дающий достаточно эффективный объектный код. До этого времени создание компиляторов было весьма "творческим" процессом. Лишь появление теории формальных языков и строгих математических моделей позволило перейти от "творчества" к "науке". Именно благодаря этому стало возможным появление сотен новых языков программирования. Более того, формальная теория компиляторов дала новый стимул развитию математической лингвистики и методам искусственного интеллекта, связанных с естественными и искусственными языками.
Основу теории компиляторов составляет теория формальных языков - весьма сложный, насыщенный терминами, определениями, математическими моделями и прочими формализмами раздел математики. Именно "языковой" стороне теории компиляторов прежде всего уделяется внимание в этом пособии. Разумеется, и формирование объектного кода, и машинно-зависимая оптимизация, и компоновка, безусловно, важны. Однако все это - частности, зависящие прежде всего от конкретной архитектуры вычислительной машины, от конкретной операционной системы. Наша же задача - научиться основам построения компиляторов. Архитектура меняется год от года, основы же остаются неизменными (на то они и основы) уже не один десяток лет.
Конечно, построить компилятор или интерпретатор можно и без всякой теории. Возможно, он даже будет работать. Но все дело в том, что, во-первых, этот титанический труд будет малоэффективен, а во-вторых, в лучшем случае мы получим "одноразовый" продукт, не пригодный для дальнейшего развития.
В пособии помимо теоретических сведений приводится ряд конкретных приемов, методов и алгоритмов. Фактически здесь содержится все то, что необходимо знать для построения одной из составляющей части компилятора - интерпретатора. Кроме того, в пособии приведен ряд примеров программ на языке Пролог. Знание Пролога является весьма желательным - уж больно просто и элегантно реализуются на нем важнейшие части компилятора. Несмотря на свой почтенный возраст, Пролог является достаточно экзотическим языком программирования, считаясь прежде всего языком искусственного интеллекта. Для создателя же компилятора Пролог - это очень удобный инструмент. В Приложении приведены некоторые сведения об этом языке, достаточные, по крайней мере, для того, чтобы понять суть приводимых примеров.
Но главное при изучении этого курса - постараться понять "анатомию" составных частей компилятора, представить себе, как можно самому реализовать тот или иной механизм. В этом смысле курс является весьма "практическим". Впрочем, и сама теория компиляторов не есть нечто искусственное, надуманное. Сначала была практика. Теория создавалась как раз для того, чтобы помочь разработчику в его практической деятельности, поэтому в любом, самом "заумном" определении, понятии и т.п. следует искать рациональное зерно.
Начнем с того, что дадим классические определения терминам, которые будут использоваться нами далее.
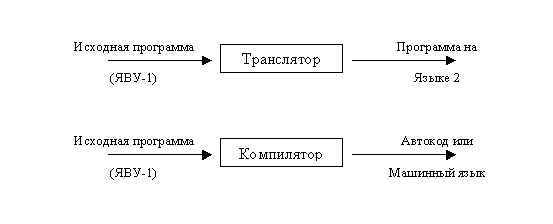
Транслятор - это программа, которая переводит текст исходной программы в эквивалентную объектную программу. Если объектный язык представляет собой автокод или некоторый машинный язык, то транслятор называется компилятором.
Автокод очень близок к машинному языку; большинство команд автокода - точное символическое представление команд машины.
Ассемблер - это программа, которая переводит исходную программу, написанную на автокоде или на языке ассемблера (что, суть, одно и то же), в объектный (исполняемый) код.
Интерпретатор принимает исходную программу как входную информацию и выполняет ее. Интерпретатор не порождает объектный код. Обычно интерпретатор сначала анализирует исходную программу (как компилятор) и транслирует ее в некоторое внутреннее представление. Далее интерпретируется (выполняется) это внутреннее представление.
Условно это можно изобразить следующим образом:

Компиляторы пишутся как на автокоде, так и на языках высокого уровня. Кроме того, существуют и специальные языки конструирования компиляторов - компиляторы компиляторов.
Компилятор компиляторов (КК) - система, позволяющая генерировать компиляторы; на входе системы - множество грамматик, а на выходе, в идеальном случае, - программа. Иногда под КК понимают язык программирования, в котором исходная программа - это описание компилятора некоторого языка, а объектная программа - сам компилятор для этого языка. Исходная программа КК - это просто формализм, служащий для описания компиляторов, содержащий, явно или неявно, описание лексического и синтаксического анализаторов, генератора кодов и других частей создаваемого компилятора. Обычно в КК используется реализация схемы т.н. синтаксически управляемого перевода. Кроме того, некоторые из них представляют собой специальные языки высокого уровня, на которых удобно описывать алгоритмы, используемые при создании компиляторов.
Ниже приведена классическая структура компилятора.
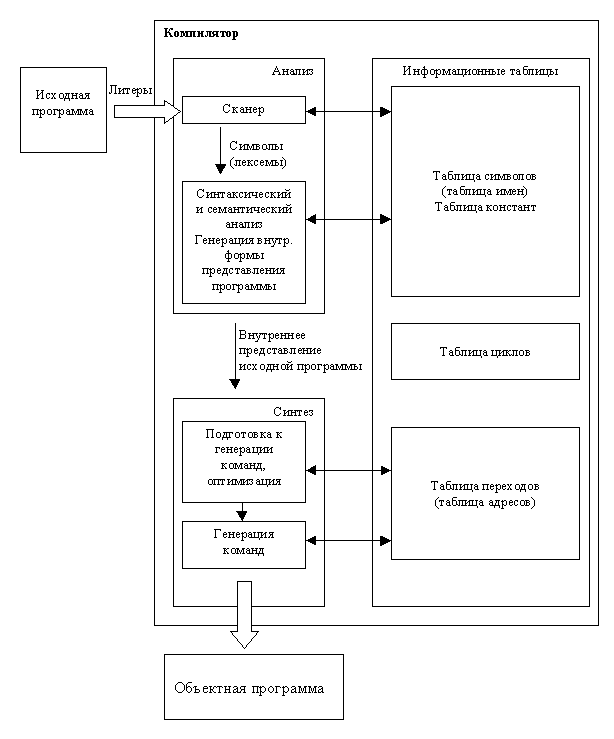
Рассмотрим далее некоторые ее составляющие.
Исходная программа - текст программы на языке высокого уровня, который должен быть переведен в машинный код.
Информационные таблицы - самостоятельные структуры, заполняющиеся в ходе лексического анализа и дополняющиеся во время работы.
Лексический анализатор (или сканер), имеющий на выходе поток лексем, нужен для того, чтобы убрать все лишнее (комментарии, разделители), выделить лексемы, т.е. лексические единицы, из которых строится машинный язык, и преобразовать их к внутренним или промежуточным формам представления. На этом этапе идет активная работа с таблицами, в которые заносится информация о распознанных лексемах, их типах, значениях и т.д. Результатом является поток лексем, эквивалентный исходному тексту.
Синтаксический анализатор необходим для того, чтобы выяснить, удовлетворяют ли предложения, из которых состоит исходная программа, правилам грамматики этого языка. Наряду с проверкой синтаксиса параллельно происходит генерация внутренней формы представления программы.
Итак, можно выделить следующие этапы компиляции:
1) Лексический анализ. Замена лексем их внутренним представлением (например, замена операторов, разделителей и идентификаторов числами).
2) Синтаксический анализ. Иногда на этом этапе также вводятся дополнительные разделители и заменяются существующие для облегчения обработки.
3) Генерация промежуточного кода (трансляция). На этом этапе осуществляется контроль типа и вида всех идентификаторов и других операндов. При этом обычно преобразование исходной программы в промежуточную (например, польскую) форму записи осуществляется одновременно с синтаксическим анализом.
4) Оптимизация кода.
5) Распределение памяти для переменных в готовой программе.
6) Генерация объектного кода и компоновка программных сегментов.
На всех этих этапах происходит работа с различного рода таблицами. В частности, для каждого блока (если таковые существуют в языке) идентификаторы, описанные внутри, запоминаются вместе со своими атрибутами. Условно все эти этапы можно изобразить следующим образом:
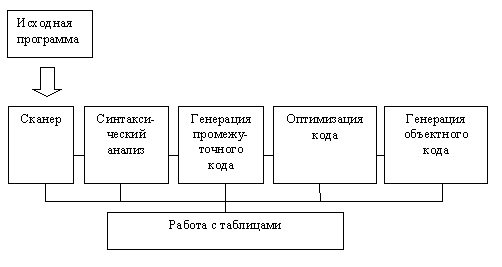
Очевидна зависимость структуры компилятора от структуры ЭВМ, точнее, от имеющейся производительности системы. Например, при малой памяти увеличивается количество проходов компиляции (т.н. многопроходные компиляторы), а при наличии памяти большого объема можно все этапы компиляции произвести за один проход (и тогда мы имеем дело с однопроходным компилятором). Тем не менее, независимо от вычислительных ресурсов, всю вышеперечисленную работу приходится так или иначе делать.
Далее мы рассмотрим вкратце некоторые из этих составных частей процесса компиляции.
На входе сканера - цепочка символов некоторого алфавита (именно так выглядит для сканера наша исходная программа). При этом некоторые комбинации символов рассматриваются сканером как единые объекты. Например:
-
один или более пробелов заменяются одним пробелом;
-
ключевые слова (вроде BEGIN, END, INTEGER и др.);
-
цепочка символов, представляющая константу;
-
цепочка символов, представляющая идентификатор (имя);
Таким образом, лексический анализатор (ЛА) группирует определенные терминальные символы (т.е. входные символы) в единые синтаксические объекты - лексемы. В простейшем случае лексема - это пара вида <тип_лексемы, значение>.
Задача выделения лексем из входного потока зачастую оказывается весьма нетривиальной и зависящей от структуры конкретного языка. Как будет интерпретироваться такая входная последовательность "567АВ"? Это может быть одна лексема (идентификатор), а может - и пара лексем - константа "567" и имя "АВ". Во втором случае либо между лексемами необходимо указание разделителя (например, пробела), либо надо заранее знать, что будет следовать дальше.
Существует два основных типа лексических анализаторов - прямые (ПЛА) и непрямые (НЛА).
Прямой ЛА определяет лексему, расположенную непосредственно справа от текущего указателя, и сдвигает указатель вправо от части текста, образующей лексему (ПЛА определяет тип лексемы, которая образована символами справа от указателя).
Непрямой ЛА определяет, образуют ли знаки, расположенные непосредственно справа от указателя, лексему этого типа. Если да, то указатель передвигается вправо от части текста, образующей лексему. Иными словами, для него заранее задается тип лексемы, и он распознает символы справа от указателя и проверяет, удовлетворяют ли они заданному типу.
У ПЛА более сложная структура - он должен выполнять больше операций, нежели НЛА. Тем не менее в большинстве современных языков программирования используется синтаксис прямых лексических анализаторов (это может быть видно по внешнему виду фраз языка).
Фортран - это классический пример языка, использующего непрямой лексический анализатор. Все дело в том, что в этом языке игнорируются пробелы. Рассмотрим, например, конструкцию
DO5I=1,10 :
Для разбора этого предложения необходим непрямой лексический анализатор, который и определит, что означает цепочка "DO5I" - идентификатор "DO5I", или же ключевое слово "DO", за которым следует метка 5, а далее - имя переменной "I". Впрочем, аналогичные неприятности ожидают и разработчиков компиляторов языков типа C или C++, в которых существуют строковые комментарии "/*:*/" и "//:". При проведении лексического анализа, встретив символ "/", изначально неясно, является ли он оператором или началом строкового комментария. И вообще, многосимвольные лексемы - штука малоприятная для анализа.
Итак, на выходе сканера - внутреннее представление имен, разделителей и т.п. Например:
Вход сканера: AVR := B + CDE; // Комментарии
Выход сканера: 38, -8, 65, -2, 184
(Если мы условимся обозначать оператор присваивания ":=" числом с кодом -8, операцию сложения - числом -2, а имена переменных числами 38, 65 и 184).
Кроме того, сканер занимается формированием различного рода таблиц. И прежде всего - таблицы имен, в которую он будет заносить распознанные имена - идентификаторы, константы, метки и т.п.
Таблица имен представляет собой структуру, подобную следующей:
|
Номер элемента |
Идентификатор |
Дополнительная информация (тип, размер и т.п.) |
|
1 |
A |
идент., тип = "строка" |
|
: |
: |
: |
|
N |
3.1415 |
константа, число |
Механизм работы с таблицами должен обеспечивать:
-
быстрое добавление новых идентификаторов и сведений о них;
-
быстрый поиск информации.
К работе с таблицами мы еще вернемся, когда будем рассматривать хеш-функции.
Синтаксический анализ - это процесс, в котором исследуется цепочка лексем и устанавливается, удовлетворяет ли она структурным условиям, явно сформулированным в определении синтаксиса языка. Это - самая сложная часть компилятора.
Синтаксический анализатор расчленяет исходную программу на составные части, формирует ее внутреннее представление, заносит информацию в таблицу символов и другие таблицы. При этом производится полный синтаксический и, по возможности, семантический контроль программы. Фактически, это - синтаксически управляемая программа. При этом обычно стремятся отделить синтаксис от семантики насколько это возможно - когда синтаксический анализатор распознает конструкцию исходного языка, он вызывает семантическую процедуру, которая контролирует эту конструкцию, заносит информацию куда надо, проверяет на дублирование описания переменных, проверяет соответствие типов и т.п.
Предложения исходной программы обычно записываются в инфиксной форме. Однако эта привычная форма, в которой оператор записывается между операндами, является совершенно не пригодной для автоматического вычисления. Дело в том, что необходимо постоянно помнить о приоритетах операторов, "забегая" при анализе выражения "вперед". К тому же очень усложняют жизнь применяемые скобки, определяющие очередность вычислений. Альтернативой инфиксной форме является польская форма записи (в честь польского математика Лукасевича): постфиксная и префиксная. Обычно под польской формой понимают именно постфиксную форму записи. Кроме того, используются и такие внутренние формы представления исходной программы, как дерево (синтаксическое) и тетрады.
Дерево. Допустим, имеется входная цепочка i=(a+b)*c. Тогда дерево будет выглядеть так:
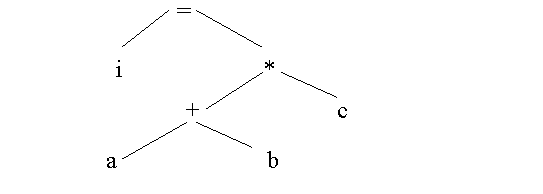
У каждого элемента дерева может быть только один "предок". Дерево "читается" снизу вверх и слева направо. Дерево - это прежде всего удобная математическая абстракция. На практике дерево можно реализовать в виде списковой структуры.
Польская форма записи. Существуют три вида записи выражений:
· инфиксная форма, в которой оператор расположен между операндами (например, "а+b");
· постфиксная форма, в которой оператор расположен после операндов (то же выражение выглядит как "а b + ");
· префиксная форма, в которой оператор расположен перед операндами ("+ а b").
Постфиксная и префиксная формы образуют т.н. польскую форму записи. Польская форма удобна прежде всего тем, что в ней отсутствуют скобки. На практике наиболее часто используется постфиксная форма. Поэтому под польской обычно понимают именно постфиксную форму записи.
В этой форме записи выражение i=(a+b)*c выглядит так: " iab+c*=". Это выражение удобно расписывается по дереву: с нижней строки записываются "a" и "b", далее "+" и "с", выше - "i" и "*" и в вершине дерева "=".
Тетрада- это четверка, состоящая из кода операции, приемника и двух операндов. Если требуется не два, а менее операторов, то в этом случае тетрада называется вырожденной. Например:
|
Исходное выражение |
Код |
Приемник |
Операнд1 |
Операнд2 |
|
a+bRT1 |
+ |
Т1 |
а |
b |
|
T1+cRT2 |
* |
T2 |
T1 |
c |
|
i=T2 |
= |
I |
T2 |
(вырожденная тетрада) |
Польская форма записи и тетрады удобны своей однозначностью. Фактически в обеих этих формах мы раскладываем исходное выражение на элементарные составляющие.
Пусть на вход синтаксического анализатора подаются выражения
"<ид1>=(<ид2>+<ид3>)*<ид4>" и "A = B+C*D"
На выходе будем иметь:
1) Дерево для выражения Дерево для выражения
"<ид1>=(<ид2>+<ид3>)*<ид4>" "A = B+C*D"
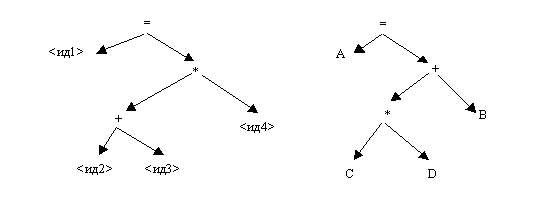
2) Тетрады для "<ид1> = (<ид2>+<ид3>)*<ид4>"
+, <ид2>, <ид3>, T1
*, T1, <ид4>, T2
=, T2, <ид1>
Тетрады для "A = B+C*D"
*, C, D, T1
+, B, T1, T2
=, T2, A
(T1, T2 - временные переменные, созданные компилятором)
3) Польская форма для "<ид1> = (<ид2>+<ид3>)*<ид4>":
<ид1> <ид2> <ид3> + <ид4> * =
Польская форма для "A=B+C*D" будет выглядеть как "ABCD*+=". Обратите внимание на то, что порядок следования операндов в польской форме записи такой же, как и в исходном инфиксном выражении (записи abc*= и bc*a= - это вовсе не одно и то же).
Алгоритм вычисления польской формы записи очень прост:
Просматриваем последовательно символы входной цепочки. Если очередной символ является операндом (идентификатором или константой), то читаем дальше. Если символ является бинарным оператором, то извлекаем из цепочки два предыдущих операнда вместе с оператором, производим операцию и помещаем результат обратно в цепочку символов.
Более подробно этот алгоритм будет рассмотрен ниже. Оставшиеся стадии компиляции, связанные с подготовкой к генерации команд, распределением памяти, оптимизацией программы и собственно с генерацией команд и генерацией объектного кода, безусловно важны, однако сейчас на них останавливаться мы не будем.
Общение на каком-либо языке - искусственном или естественном- заключается в обмене предложениями или, точнее, фразами. Фраза - это конечная последовательность слов языка. Фразы необходимо уметь строить и распознавать.
Если существует механизм построения фраз и механизм признания их корректности и понимания (механизм распознавания), то мы говорим о существовании некоторой теории рассматриваемого языка.
Определение: Язык L - это множество цепочек конечной длины в алфавите S.
Возникает вопрос - каким образом можно задать язык? Во-первых, язык можно задать полным его перечислением. С точки зрения математики это вовсе не является полной бессмысленностью. А во-вторых, можно иметь некоторое конечное описание языка.
Одним из наиболее эффективных способов описания языка является грамматика. Строго говоря, грамматика - это математическая система, определяющая язык. Как мы убедимся далее, грамматика пригодна не только для задания (или генерации) языка, но и для его распознавания.
Далее нам потребуются некоторые термины и обозначения. Начнем с определения замыкания множества.
Если å - множество (алфавит или словарь), то å* - замыкание множества å, или, иначе, свободный моноид, порожденный å, т.е. множество всех конечных последовательностей, составленных из элементов множества å, включая и пустую последовательность.
Например, пусть A = {a, b, c}. Тогда A*={e, a, b, c, aa, ab, ac, bb, bc, cc, :}. Здесь e - это пустая последовательность.
Символом å+ мы будем обозначать положительное замыкание множества å (или, иначе, свободную полугруппу, порожденную множеством å). В отличие от свободного моноида в положительное замыкание не входит пустая последовательность.
Теперь все готово к тому, чтобы дать основное определение.
Определение. Грамматика - это четверка G = (N, S,P,S), где
N - конечное множество нетерминальных символов (синтаксические переменные или синтаксические категории);
S - конечное множество терминальных символов (слов) (SÇN=Æ);
P - конечное подмножество множества
(NÈS)*N(NÈS)* ´ (NÈS)*
Элемент (a,b) множества P называется правилом или продукцией и записывается в виде aRb;
S - выделенный символ из N (SÎN), называемый начальным символом (эта особая переменная называется также "начальной переменной" или "исходным символом").
Пример:
G = ({A,S},{0,1},P,S),
P = (SR0A1, 0AR00A1, ARe)
Определение. Язык, порождаемый грамматикой G (обозначим его через L(G)) - это множество терминальных цепочек, порожденных грамматикой G.
Или, иначе, язык L, порождаемый (распознаваемый) грамматикой, есть множество последовательностей (слов), которые
- состоят лишь из терминальных символов;
- можно породить, начиная с символа S.
И опять нам требуются определения и обозначения:
Определение: Пусть G = (N, S, P, S). Отношение ÞG на множестве (NÈS)* называется непосредственной выводимостью jÞGy (y непосредственно выводима из j), если abg - цепочка из (NÈS)* и bRd - правило из P, то abgÞGadg.
Транзитивное замыкание отношения ÞG обозначим через Þ+G.
Запись jÞ+G y означает: y выводима из j нетривиальным образом.
Рефлексивное и транзитивное замыкание отношения ÞG обозначим через Þ*G. Запись jÞ*G y означает: y выводима из j. (Если Þ* - это рефлексивное и транзитивное замыкание отношения Þ, то последовательность a1Þa2, a2Þa3,.., am-1Þam, где aiÎ(NÈS)*, записывается так: a1Þ*am.)
При этом предполагалось наличие следующих определений:
Определение A. k-я степень отношения R на множестве A (Rk):
(1) aR1b тогда и только тогда, когда aRb (или R1ºR);
(2) aRib для i>1 тогда и только тогда, когда $ cÎA: aRc и cRi-1b.
Определение B. Транзитивное замыкание отношения R на множестве A (R+):
aR+b тогда и только тогда, когда aRib для некоторого i>0.
Определение C. Рефлексивное и транзитивное замыкание отношения R на множестве A (R*):
(1) aR*a для " aÎA;
(2) aR*b, если aR+b
Таким образом, получаем формальное определение языка L:
L(G)={w| wÎå*, SÞ*w}
Нормальная форма Бэкуса-Наура. Нормальная форма Бэкуса-Наура (НФБ или БНФ) служит для описания правил грамматики. Она была впервые применена Науром при описании синтаксиса языка Фортран. По сути БНФ является альтернативной, более упрощенной, менее строгой и потому более распространенной формой записи грамматики. Далее мы будем пользоваться ею наравне с формальными определениями в силу ее большей наглядности.
Пример:
<число> ::= <чс>
<чс> ::= <чс><цифра>|<цифра>
<цифра> ::= 0|1|...|9
Вернемся к определению грамматики как четверки вида G = (N, å, P, S), где нас интересует вид правил P, под которыми понимается конечное подмножество множества
(NÈS)*N(NÈS)* ´ (NÈS)*
В зависимости от конкретики реализаций правил P существует следующая классификация грамматик (в порядке убывания общности вида правил):
Грамматика типа 0: Правила этой грамматики определяются в самом общем виде.
P: xUyRz
Для распознавания языков, порожденных этими грамматиками, используются т.н. машины Тьюринга - очень мощные (на практике практически неприменимые) математические модели.
Грамматика типа 1: Контекстно-зависимые (чувствительные к контексту)
P: xUyRxuy
Грамматика типа 2: Контекстно-свободные. Распознаются стековыми автоматами (автоматами с магазинной памятью)
P: URu
Грамматика типа 3: Регулярные грамматики. Распознаются конечными автоматами
P: URa или URaA
При этом приняты следующие обозначения:
u Î (NÈS)+
x, y, z Î (NÈS)*
A,U Î N
a Î S
Условно иерархию Хомского можно изобразить так:
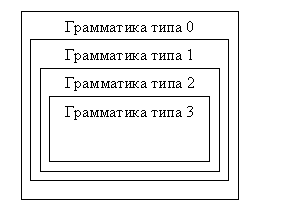
Итак, иерархия Хомского необходима для классификации грамматик по степени их общности. При этом, как видно,
· Грамматика типа 0 - самая сложная, никаких ограничений на вид правил в ней не накладывается.
· Грамматика типа 1 - контекстно-зависимая; в ней возможность замены цепочки символов может определяться ее (т.е. цепочки) контекстом.
· Грамматика типа 2 - контекстно-свободная; в левой части нетерминалы меняются на что угодно.
· Грамматика типа 3 - регулярная грамматика, самая ограниченная, самая простая.
Начнем изучение грамматик с самого простого и самого ограниченного их типа - регулярных грамматик. Вот некоторые примеры:
1. Идентификатор (в форме БНФ)
<идент> ::= <бкв>
<идент> ::= <идент><бкв>
<идент> ::= <идент><цфр>
<бкв> ::= a|b|...|z
<цфр> ::= 0|1|...|9
2. Арифметическое выражение (без скобок)
G = (N, å,P,S)
N={S,E,op,i}
å={<число>, <идент>,+,-,*,/}
P={SRi
SRiE
ERop S
opR+
opR-
opR*
opR/
iR<число>
iR<идент>}
Ту же грамматику бесскобочных выражений можно изобразить в виде БНФ (это не совсем строго, зато весьма наглядно):
<expr> ::= <число>|<идент>
<expr> ::= <expr><op><expr>
<op> ::= +|-|*|/
<число> ::= <цфр>
<число> ::= <число><цфр>
3. Еще один пример:
Z ::= U0 | V1
U ::= Z1 | 1
V ::= Z0 | 0
Порождаемый этой грамматикой язык состоит из последовательностей, образуемых парами 01 или 10, т.е. L(G) = { Bn | n > 0}, где B = { 01, 10}.
Стоит, однако, рассмотреть чуть более сложный объект (например, арифметические выражения со скобками), как регулярные грамматики оказываются слишком ограниченными:
4. Арифметическое выражение (со скобками)
G0=({E,T,F},{a,+,*,(,),#},P,E)
P = { E R E+T|T
T R T*F|F
F R (E)|a}
Это, разумеется, уже не регулярная, а контекстно-свободная грамматика.
Тем не менее регулярные грамматики играют очень важную роль в теории компиляторов. По крайней мере их достаточно для того, чтобы реализовать первую часть компилятора - сканер. Ведь сканер имеет дело именно с такими простыми объектами, как идентификаторы и константы.
Итак, будем считать, что мы как минимум умеем порождать фразы регулярных языков. Однако все-таки нашей основной задачей является не порождение, а распознавание фраз. Поэтому далее рассмотрим один из наиболее эффективных распознающих механизмов - конечный автомат.
Как уже говорилось выше, грамматика - это порождающая система. Автомат - это формальная воспринимающая система (или акцептор). Правила автомата определяют принадлежность входной формы данному языку, т.е. автомат - это система, которая распознает принадлежность фразы к тому или иному языку.
Говорят, что автомат эквивалентен данной грамматике, если он воспринимает весь порождаемый ею язык и только этот язык. Как и грамматики, автоматы определяются конечными алфавитами и правилами переписывания.
Определение. Конечный автомат (КА) - это пятерка КА = (å,Q,q0,T,P), где
· å - входной алфавит (конечное множество, называемое также входным словарем);
· Q - конечное множество состояний;
· q0 - начальное состояние (q0ÎQ);
· T - множество терминальных (заключительных) состояний, TÌQ;
· P - подмножество отображения вида Q´åRQ, называемое функцией переходов. Элементы этого отображения называются правилами и обозначаются как
qiakRqj, где qi и qj - состояния, ak - входной символ: qi, qj Î Q, akÎå.
КА можно рассматривать как машину, которая в каждый момент времени находится в некотором состоянии qÎQ и читает поэлементно последовательность w символов из å, записанную на конечной слева ленте. При этом читающая головка машины двигается в одном направлении (слева направо), либо лента перемещается (справа налево). Если автомат в состоянии qi читает символ ak и правило qiakRqj принадлежит P, то автомат воспринимает этот символ и переходит в состояние qj для обработки следующего символа:
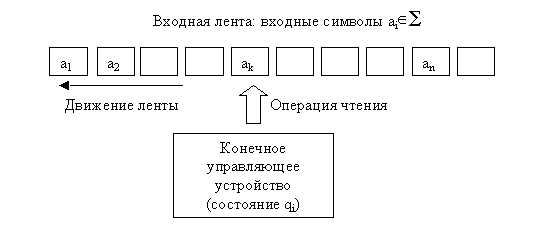
Таким образом, суть работы автомата сводится к тому, чтобы прочитать очередной входной символ и, используя соответствующее правило перехода, перейти в другое состояние.
Связь между конечными автоматами и регулярными грамматиками самая непосредственная, что следует из утверждения:
Каждой грамматике можно поставить в соответствие эквивалентный ей автомат, и каждому автомату соответствует эквивалентная ему грамматика.
Итак, мы установили взаимосвязи между грамматиками, языками и автоматами:
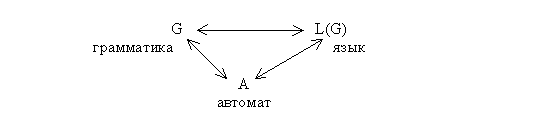
Конфигурация конечного автомата - это элемент множества Q´å*, т.е. последовательность вида qw, где q - состояние из Q, w - элемент из å*.
Если к любой конфигурации qiw применимо не более одного правила, то такой автомат называется детерминированным конечным автоматом (ДКА). В противном случае мы имеем дело с недетерминированным конечным автоматом (НКА).
Итак, недетерминированные конечные автоматы отличаются от ДКА
- неоднозначностью переходов;
- наличием, в общем случае, более чем одного начальных состояний.
КА удобно представлять в виде диаграммы состояний (переходов), представляющей собой ориентированный граф.
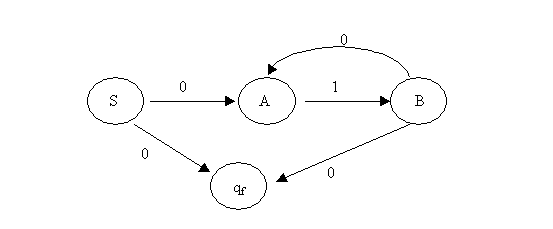
Пример 1. Пусть задан следующий НКА
КА = (å,Q,q0,T,P)
å = {0,1},
Q = {S,A,B,qf},
q0 = S,
T = {qf},
P = {S0Rqf, S0RA, A1RB, B0Rqf, B0RA}
Диаграмма его переходов будет выглядеть так:
Пример 2. Рассмотрим понятие идентификатора, представленное в НФБ и в виде ДКА:
<идент> ::= <бкв>
<идент> ::= <идент><бкв>
<идент> ::= <идент><цфр>
<бкв> ::= a|b|...|z
<цфр> ::= 0|1|...|9
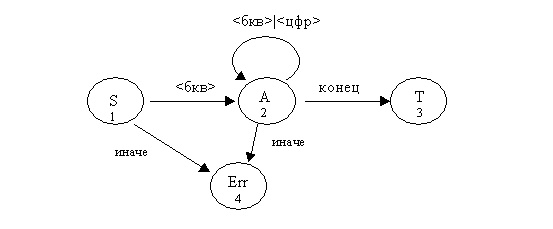
Изобразим множество P в виде матрицы (т.н. матрицы переходов)
P:
|
|
1 |
2 |
3 |
|
<бкв> |
2 |
2 |
- |
|
<цфр> |
4 |
2 |
- |
|
<конец> |
4 |
3 |
- |
|
<иначе> |
4 |
- |
- |
Строки матрицы - входные символы, столбцы - состояния автомата. Некоторые элементы этой матрицы - явно лишние. В частности, 3-й столбец вовсе не нужен. Эти "лишние" состояния могут служить для диагностики ошибок.
Обобщенный алгоритм работы этого автомата может быть реализован на языке С следующим образом:
char c; //текущий исходный символ
int q; //номер состояния
int a; //входной текущий символ для автомата
q=0; //начальное состояние автомата
while(1) //бесконечный цикл
{ c = readchar(); //считывание входного символа
a = gettype(c); //распознавание входного символа -
//отнесение его к одной из известных автомату
//категорий - <бкв>, <цфр>, <конец> или <иначе>
//Выполнение перехода
q = P[a, q];
//Обработка
if (q==3) return 1; //нормальный выход из программы
if (q==4) return 0; //выход по ошибке
}
Обратите внимание на то, что входной алфавит - это то, что автомат умеет воспринимать. При этом он не обязан различать между собой, скажем, буквы и цифры.
Пример 3. Арифметическое выражение (без скобок)
<expr> ::= <число>|<идент>
<expr> ::= <expr><op><expr>
<op> ::= +|-|*|/
<число> ::= <цфр>
<число> ::= <число><цфр>
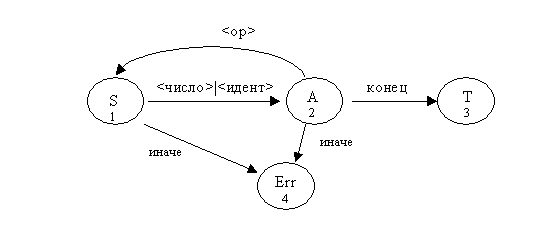
Рассмотрим анализатор языка, распознаваемый КА, структура которого приведена ниже:
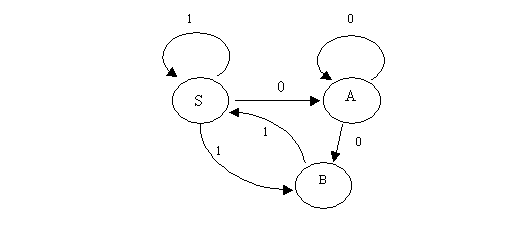
Автомат этот недетерминированный и его реализация с помощью процедурных языков программирования может вызвать определенные сложности. Обратимся поэтому к языку Пролог:
/*
АНАЛИЗАТОР РЕГУЛЯРНОЙ ГРАММАТИКИ - 1
S->1S
S->1B
S->0A
A->0A
A->0B
B->1S
Начальное состояние S
Конечное состояние B
*/
goal
Recognize([1,1,1,1,1,0,0,0,0,0,0,1,1,0,0,0,0]).
clauses
Recognize(L) :- s(L), write("ФРАЗА РАСПОЗНАНА").
Recognize(_) :- write("*** ОШИБКА ! ФРАЗА НЕ РАСПОЗНАНА").
append([],L,L).
append([H|T],B,[H|C]) :- append(T,B,C).
S(L) :- append(L1,L2,L), L1=[1], S(L2).
S(L) :- append(L1,L2,L), L1=[1], B(L2).
S(L) :- append(L1,L2,L), L1=[0], A(L2).
A(L) :- append(L1,L2,L), L1=[0], A(L2).
A(L) :- append(L1,L2,L), L1=[0], B(L2).
B(L) :- append(L1,L2,L), L1=[1], S(L2).
B([]).
Более эффективным и простым будет следующий вариант программы, в которой нет необходимости использовать процедуру деления списка на две части:
/* АНАЛИЗАТОР РЕГУЛЯРНОЙ ГРАММАТИКИ - 2 . Вариант без предиката append */
goal
Recognize([1,1,1,1,1,0,0,0,0,0,0,1,1,0,0,0,0]).
clauses
Recognize(L) :- s(L), write("ФРАЗА РАСПОЗНАНА").
Recognize(_) :- write("*** ОШИБКА ! ФРАЗА НЕ РАСПОЗНАНА").
S([1|L]) :- S(L).
S([1|L]) :- B(L).
S([0|L]) :- A(L).
A([0|L]) :- A(L).
A([0|L]) :- B(L).
B([1|L]) :- S(L).
B([]).
Вернемся к вопросу о конечных состояниях. Смысл конечного состояния заключается в определении условия завершения работы автомата. Работа автомата может быть завершена при попадании его в одно из заключительных состояний (такие состояния назовем поглощающими), и тогда мы имеем дело с ПЛА. Однако условие завершения может быть более сложным: работа автомата заканчивается тогда, когда входная последовательность исчерпана и при этом автомат находится в одном из терминальных состояний. Эта ситуация характерна для НЛА.
Реализовать недетерминированный автомат на Прологе достаточно просто. А сделать то же самое на процедурном языке - задача весьма нетривиальная. На практике поэтому предпочтительнее работать с "нормальным", детерминированным автоматом, не допускающим неоднозначностей.
Обычно при описании тех или иных объектов наличие дополнительных ограничений снижает общность. Однако большая общность НКА по сравнению с ДКА является кажущейся. Дело в том, что справедливо следующее утверждение:
Для любого НКА можно построить эквивалентный ему конечный детерминированный автомат.
Для построения детерминированного автомата можно воспользоваться следующей теоремой:
Теорема. Пусть НКА F= (å,Q,q0,T,P) допускает множество цепочек L. Определим ДКА F'= (å',Q',q0',T',P') следующим образом:
1) Множество состояний Q' состоит из всех подмножеств множества Q. Обозначим элемент множества Q' через [S1,S2,..,Sl], где S1,S2,..,SlÎQ.
2) å' = å.
3) Отображение P' определяется как
P'([S1,S2,..,Sm],x) = [R1,R2,..,Rm],
где P({S1,S2,..,Sm },x) = { R1,R2,..,Rm }, Si,RiÎQ, xÎå.
4) Пусть q0={S1,S2,..,Sk}.
Тогда q0'=[S1,S2,..,Sk].
5) Пусть множество заключительных состояний T={Sj, Sk,.., Sn}.
Тогда T'=[Sj, Sk,.., Sn].
Или, иначе,
T'={t=[Sa,Sb,..,Sc] | $ Sb: SbÎT}.
Построенный таким образом детерминированный конечный автомат будет эквивалентен в смысле "вход-выход" исходному НКА.
Приведем пример построения ДКА по НКА. Пусть дан недетерминированный автомат
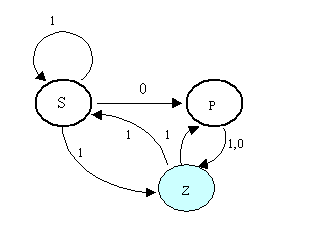
Правила переходов: {S1RS, S1RZ, S0RP, P1RZ, P0RZ, Z1RP, Z1RS}.
Начальные состояния: {S, P}.
Заключительные состояния: {Z}.
Множество состояний ДКА будет таким: {S, P, Z, PS, SZ, PSZ, PZ}. Их будет ровно 2n-1, где n - количество состояний исходного автомата.
Его правила переходов:
{S1RSZ, S0RP, P1RZ, P0RZ, Z1RPS, PS1RSZ, PS0RPZ, SZ1RPSZ, PSZ1RPSZ, PZ1RPSZ}.
Начальное состояние: SP.
Заключительные состояния: {Z, PZ, SZ, PSZ}.
Тогда детерминированный автомат будет выглядеть так:
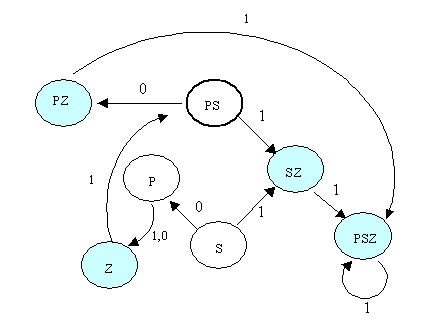
После упрощения автомата, т.е. удаления вершин, не достижимых из начальной, получим такой автомат:
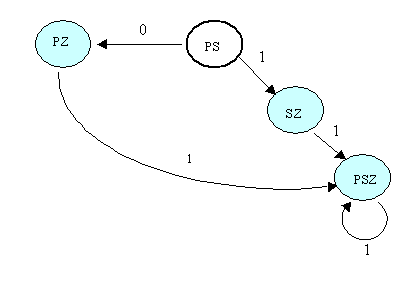
Завершая рассуждения о недетерминированных автоматах, следует отметить еще один момент, связанный с множеством начальных состояний (н.с.) в НКА. Дело в том, что когда имеется несколько н.с., работа автомата заключается в том, что переход по входному символу осуществляется одновременно из всех начальных состояний. Именно в этом заключается суть процедуры объединения всех н.с. в одно. Это особенно важно при моделировании НКА, скажем, средствами Пролога.
Итак, теперь все готово к тому, чтобы приступить к построению сканера. Напомним, что нам необходимо построить лексический анализатор для выделения из входного потока исходных составляющих языка - лексем или символов. Символами являются:
- разделители или операторы (+,-,*,/,(,) и т.п.);
- служебные слова (что-то вроде begin, end,... и т.п.);
- идентификаторы;
- числа.
Кроме того, необходимо исключать комментарии (как строчные, типа '//', так и многострочные, вида '/*...*/').
Строить сканер мы будем, используя конечный автомат. К автомату предъявляются следующие минимальные требования:
1. Автомат должен формировать поток лексем;
2. Автомат должен заносить полученные лексемы в таблицу символов или имен.
Наш распознающий автомат упрощенно может выглядеть следующим образом:
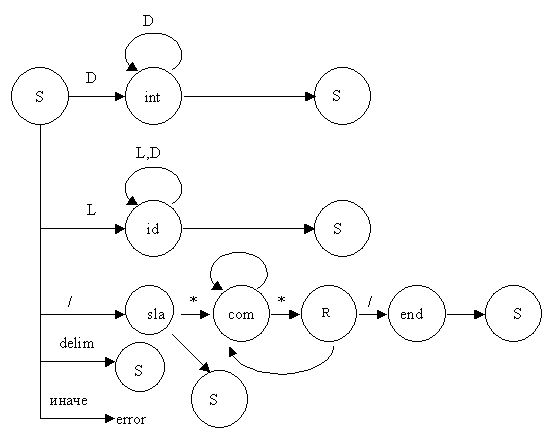
Здесь под символом D понимается цифра, L означает букву, а delim - разделитель (пробел, табуляцию и т.п.). Состояние int отвечает за распознавание числа, id - за распознавание имени, а sla, com, end и R - за распознавание комментариев. Чтобы не загромождать схему дугами, переходы в основное состояние S обозначены дублированием этой вершины.
При этом следует отметить, что
1. При переходе в начальное состояние S иногда требуется возвращать обратно считываемый символ входной последовательности, т.е. необходимо сместить указатель на одну позицию назад. Иначе мы просто будем терять часть лексем, т.к. автомат --это устройство, последовательно считывающее очередной входной символ на каждом такте работы.
2. Автомат в таком виде бесполезен, он не выполняет никаких полезных процедур.
Следовательно, автомат необходимо дополнить процедурной частью. Именно процедурная часть отвечает за формирование имен, которые далее будут заноситься в таблицу символов, за возврат считанного символа обратно во входной поток, за инициализацию и т.д. Дополнение автомата этой процедурной частью автомата заключается в том, что когда автомат совершает очередной переход, должна выполняться связанная с этим переходом одна или несколько процедур (или подпрограмм). Это, разумеется, несколько усложняет структуру автомата, однако эту работу выполнять необходимо, т.к. мы занимаемся не только проверкой входной последовательности, но и ее преобразованием в поток лексем.
При трансляции программы для каждого нового идентификатора в таблицу символов добавляется элемент. Однако поиск элементов ведется всякий раз, когда встречается этот идентификатор. Так как на этот процесс уходит много времени, необходимо выбрать такую организацию таблиц, которая допускала бы прежде всего эффективный поиск.
Простейший способ организации - использовать неупорядоченную таблицу. Новый элемент добавляется в таблицу в порядке поступления. Среднее время поиска пропорционально n/2 (в среднем приходится делать n/2 сравнений).
Элементы таблицы можно отсортировать. Тогда можно использовать процедуру бинарного поиска, при котором максимальное число сравнений будет равно 1+log2n. Однако сортировка - это слишком трудоемкая процедура для того, чтобы ее использовать при организации таблиц.
Идеальный вариант - уметь по имени сразу определить адрес элемента. В этом смысле "хорошей" процедурой поиска является та, которая сможет определить хотя бы приблизительный адрес элемента. Одним из наиболее эффективных и распространенных методов реализации такой процедуры является хеш-адресация.
Хеш-адресация - это метод преобразования имени в индекс элемента в таблице. Если таблица состоит из N элементов, то им присваиваются номера 0,1,..,N-1. Тогда назовем хеш-функцией некоторое преобразование имени в адрес. Простейший вариант хеш-функции - это использование внутреннего представления первой литеры имени.
Пока для двух различных символов результаты хеширования различны, время поиска совпадает с временем, затраченным на хеширование. Однако, все проблемы начинаются тогда, когда результаты хеширования совпадают для двух и более различных имен. Эта ситуация называется коллизией.
Хорошая хеш-функция распределяет адреса равномерно, так что коллизии возникают не слишком часто. Но прежде, чем говорить о реализации хеш-функций, обратимся к вопросу о том, каким образом разрешаются коллизии.
Пусть хешируется имя S и при этом обнаруживается коллизия. Обозначим через h значение хеш-функции. Тогда сравниваем S с элементом по адресу (h+p1)mod N, где N - длина таблицы (максимальное число элементов в таблице). Если опять возникает коллизия, то выбираем для сравнения элемент с адресом (h+p2)mod N и т.д. Это будет продолжаться до тех пор, пока не встретится элемент (h+pi)mod N, который либо пуст, либо содержит S, либо снова является элементом h (pi=0, и тогда считается, что таблица полна).
Способы рехеширования заключаются в выборе чисел p1,p2,..,pn. Рассмотрим наиболее распространенные из них.
Для начала введем параметр, называемый коэффициентом загрузки таблицы lf:
lf = n/N, где
n - текущее количество элементов в таблице, N - максимально возможное число элементов.
Линейное рехеширование
pi = i (т.е. p1=1, p2=2,..,pn=n).
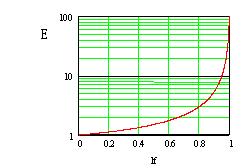
Среднее число сравнений E при коэффициенте загрузки lf определяется как
E(lf) = (1-lf/2)/(1-lf).
Это - очень неплохой показатель. В частности, при 10-ти процентной загрузке имеем E, равное 1.06, при 50-ти процентном заполнении E равно всего 1.5, а при 90 процентах загрузки требуется сделать в среднем всего 5.5 сравнений.
Ниже приведен график этой функции:
Случайное рехеширование
Пусть максимальное число элементов в таблице кратно степени двойки, т.е. N=2k. Вычисление pi осуществляется по следующему алгоритму:
1) R := 1
2) Вычисляем pi:
a) R := R*5
b) выделяем младшие k+2 разрядов R и помещаем их в R
c) pi := R>>1 (сдвигаем R вправо на 1 разряд)
3) Перейти к П.2
Среднее число сравнений E при коэффициенте загрузки lf
E = -(1/lf)log2(1-lf)
Рехеширование сложением
pi = i(h+1), где h - исходный хеш-индекс.
Этот метод хорош для N, являющихся простыми числами.
Как уже говорилось, хеш-адресация - это преобразование имени в индекс. Имя представляет множество литер (символов), и для вычисления индекса поступают обычно следующим способом:
1) Берется S', являющееся результатом суммирования литер из исходного символа S (либо простое суммирование, либо поразрядное исключающее ИЛИ):
![]()
2) Вычисляется окончательный индекс. При этом возможны самые различные варианты. В частности:
a) Умножить S' на себя и использовать n средних битов в качестве значения h (для N=2n);
b) Использовать какую-либо логическую операцию (например, исключающее ИЛИ) над некоторыми частями S';
c) Если N=2n, то разбить S' на n частей и просуммировать их. Использовать n крайних правых битов результата;
d) Разделить S' на длину таблицы, и остаток использовать в качестве хеш-индекса.
Итак, хорошая хеш-функция - это та, которая дает как можно более равномерное и случайное распределение индексов по именам, т.е. для "похожих" или "близких" имен хеш-функция должна выдавать сильно разнящиеся индексы, т.е. не допускает группировки имен в таблице символов.
Приведем пример фрагмента программы, реализующей хеш-адресацию:
struct name //элемент таблицы символов
{ char *string; //имя
name *next; //ссылка на следующий элемент
double value; //значение
};
const TBLSIZE = 23; // Количество "ящиков", по которым раскладываем символы
name *table[TBLSIZE];
name *findname(char *str, int ins)
// Функция поиска в таблице имени name
// Если ins!=0, то происходит добавление элемента в таблицу
{ int hi = 0; //Это, фактически, наш хеш-индекс
char *pp = str;
// Суммируем по исключающему ИЛИ каждый символ строки.
// Далее сдвигаем для того, чтобы индекс был лучше
// (исключаем использование только одного байта)
while (*pp)
{ hi<<=1;
hi^= *pp++;
}
if (hi<0) hi = -hi;
//Берем остаток
hi %= TBLSIZE;
//Поиск. Мы нашли список, теперь используем
// метод линейного рехеширования
for(name *n=table[hi];n;n=n->next)
if(strcmp(str,n->string)==0) return n; //Нашли. Возвращаем адрес
//Ничего не нашли
if(ins==0) return NULL; // error("Имя не найдено")
//Добавляем имя
name *nn = new name;
nn->string = new char[strlen(str)+1];
strcpy(nn->string, str);
nn->value = 0;
nn->next = table[hi];
table[hi] = nn;
return nn;
}
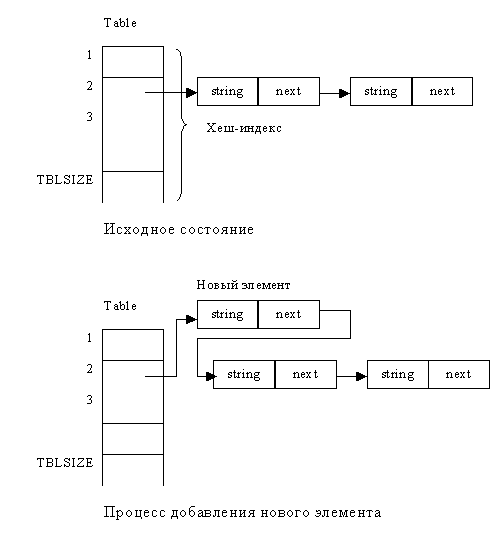
В данном примере таблица символов представляет собой не линейный список, а множество списков, адреса начала которых содержатся в некотором массиве. (Представьте себе аналогию с множеством ящиков, в которых и осуществляется поиск. Тогда хеш-индекс будет представлять собой номер некоторого ящика.)
Условно механизм работы с подобной организацией таблицы символов можно изобразить так:
Следующей по сложности за регулярной грамматикой следует контекстно-свободная (context-free) грамматика (КСГ)
Естественно, определение КСГ внешне выглядит как и обычное определение грамматики: Gксг = (N, S, P, S), однако при этом характерным для КСГ является форма ее правил (продукций)
P: ARa,
где AÎN, aÎ (NÈS)+.
В качестве примера рассмотрим, как мог бы выглядеть некий командный, внешне приближенный к естественному язык:
N = {группа_существ, глагол, прилагательное, существительное, предлог, фраза}
S = {печатать, стереть, зеленый, первый, последний, символ, строка, страница, в}
S = фраза
P = { ФрR Г, Гс
ГсR Прил, С
ГсR Прил, С, Предлог, Гс
ГRпечатать
ГRстереть
ПрилRзеленый
ПрилRпервый
ПрилRпоследний
СRсимвол
СRстрока
СRстраница
ПредлогRв}
Эта грамматика может порождать фразы вроде "Печатать зеленый строка", "Стереть первый символ в последний строка в первый страница" и т.п. Синтаксическая проверка подобных предложений может быть осуществлена путем простого перебора возможных подстановок правил грамматики. Например, анализатор предложений такого языка на Прологе может выглядеть так:
/*
АНАЛИЗАТОР КС-ГРАММАТИКИ
Фраза -> Глагол, Группа_сущ
Группа_сущ -> Прилагат, Существ
Группа_сущ -> Прилагат, Существ, Предлог, Группа_сущ
Глагол -> ...
Прилагат -> ...
Существ -> ...
Предлог -> ...
*/
goal
FRAZA = ["печатать","первый","символ","в","последний","строка"],
write("\nРАЗБОР ПРЕДЛОЖЕНИЯ\n"), print_list(FRAZA),
s(FRAZA).
clauses
s(A) :- sentence(A), write("\nФРАЗА РАСПОЗНАНА\n").
s(_) :- write("\nОШИБКА: ФРАЗА НЕ РАСПОЗНАНА\n").
% СЛУЖЕБНЫЕ И СЕРВИСНЫЕ ПРЕДИКАТЫ
append([],L,L).
append([H|A],B,[H|C]) :- append(A,B,C).
print_list([]).
print_list([Head|Tail]) :- write(Head,"."), print_list(Tail).
% СИНТАКСИС
sentence(S) :-
append(S1,S2,S),
glagol(S1),
GS(S2),
write("\nГлагол:"), writel(S1),
write("\nГс: "), writel(S2).
GS(S) :-
append(S1,S2,S),
prilagat(S1),
noun(S2),
write("\n*** Разбор ГС-1:"),
write("\nПрилагательное: "),writel(S1),
write("\nСуществительное:"),writel(S2).
GS(S) :-
append(S1,Stmp1,S),
append(S2,Stmp2,Stmp1),
append(S3,S4,Stmp2),
prilagat(S1),
noun(S2),
predlog(S3),
GS(S4),
write("\n*** Разбор ГС-2:"),
write("\nПрилагательное: "), print_list(S1),
write("\nСуществительное:"), print_list(S2),
write("\nПредлог: "), print_list(S2),
write("\nГс: "), print_list(S2).
% СЛОВАРЬ
noun([символ]). noun([строка]). noun([страница]).
glagol([печатать]). glagol([стереть]).
prilagat([первый]). prilagat([второй]). prilagat([последний]).
predlog([в]).
Но это все - "экзотика". Теперь рассмотрим более осмысленный пример - грамматику арифметических выражений. Эта грамматика в различных вариантах нам будет встречаться и далее. Пока же рассмотрим наиболее простой случай, содержащий лишь две бинарные операции с разными приоритетами.
G0=({E,T,F},{a,+,*,(,)},P,E)
P = { E R E+T|T
T R T*F|F
F R (E)|a}
Анализатор на Прологе будет выглядеть так:
E(L) :- T(L).
E(L) :- a3(L1,["+"],L3,L),
E(L1),
T(L3).
T(L) :- F(L).
T(L) :- a3(L1,["*"],L3,L),
T(L1), F(L3).
F(L) :- L=["a"].
F(L) :- a3(["("],L2,[")"],L),
E(L2).
Здесь предикат a3() разбивает список на три части. Как видно, Пролог-программа повторяет нашу грамматику с точностью до формы записи.
Несмотря на кажущуюся общность КСГ, при описании естественно-подобных языков существуют ограничения, связанные с различного рода бесконтекстными согласованиями (рода, падежа, числа и т.п.).
Для решения проблемы подобных согласований можно ввести еще одну разновидность грамматик - грамматики определенных клауз. Их особенностью является наличие контекстуальных аргументов.
Рассмотрим, каким образом может осуществляться согласование родов. Допустим, у нас есть группа существительных (ГС), состоящая из местоимения (Мест), прилагательного (Прил) и существительного (Сущ). Тогда определение ГС, учитывающее согласование родов, может выглядеть так:
Гс R Мест(k), Прил(k), Сущ(k), ГС
При этом k является контекстуальным аргументом, отвечающим за согласование родов. Этот аргумент является логической переменной:
Мест(муж) R этот
Мест(жен) R эта
Прил(муж) R второй
Прил(жен) R вторая
Сущ(жен) R строка
Сущ(муж) R пароль
и т.д.
На Прологе введение контекстуального аргумента выглядит так:
mest("муж","этот").
pril ("жен", "вторая").
и т.п.
До сих пор мы занимались лишь проблемами анализа - лексического и синтаксического. Настало время решать и основную нашу задачу - задачу синтеза. Выше уже упоминалось о том, что обычно эти две задачи решаются одновременно. Посмотрим, как это происходит.
Рассмотрим еще раз грамматику арифметического выражения.
SRE
ERT
ERE+T
TRF
TRT*F
FRa
FR(E)
где E-выражение,
T-терм,
F-формула,
a-идентификатор.
Наша первая задача состоит в том, чтобы проанализировать входную фразу и понять, является ли она синтаксически правильной. Для этого можно заняться простым перебором возможных вариантов применения наших правил грамматики, начиная с самого верхнего (начального) символа S. И перебирать варианты мы будем до тех пор, пока не получится фраза, состоящая только из терминальных символов. Это - так называемый левый вывод цепочки.
Например, пусть дана фраза: a+a*a. Воспользовавшись данной грамматикой, получим следующую цепочку вывода:
SRERE+TRE+T*FRT+T*FRF+F*FRa+a*a
Следовательно, эта фраза принадлежит нашему языку. Но кроме того, нам хотелось бы, помимо анализа, сделать еще что-нибудь полезное. Например, сформировать попутно какую-нибудь внутреннюю форму представления этой фразы (коли она является корректной).
Для этого можно использовать следующий прием: применение каждого правила грамматики будет вызывать выполнение той или иной семантической процедуры. Именно в этом заключается основная идея синтаксически управляемого перевода.
Рассмотрим схему перевода, отображающего арифметические выражения из языка L(G0) в соответствующие постфиксные польские записи.
Судя по определению постфиксной формы записи, правилу ERE+T соответствует элемент перевода E=ET+ (Выражению E+T в польской форме соответствует запись ET+). Строго говоря, элемент перевода E=ET+ означает, что перевод, порождаемый символом E, стоящим в левой части правила, получается из перевода, порождаемого символом E, стоящим в правой части правила, за которым идут перевод, порожденный символом T, и знак +. Рассуждая подобным образом, получим в результате следующую схему перевода:
|
Правило |
Элемент перевода |
|
ERE+T |
E = ET+ |
|
ERT |
E = T |
|
TRT*F |
T = TF* |
|
TRF |
T = F |
|
FR(E) |
F = E |
|
FRa |
F = a |
Определим выход, соответствующий входу a+a*a. Для этого сначала по правилам схемы перевода найдем левый вывод цепочки a+a*a из S. Затем вычислим соответствующую последовательность выводимых пар цепочек. При этом будем дописывать справа от полученной последовательности результат применения соответствующего элемента перевода:
(E,E) Þ (E+T, ET+)
Þ (T+T, TF+)
Þ (F+T, FT+)
Þ (a+T, aT+)
Þ (a+T*F, aTF*+)
Þ (a+F*F, aFF*+)
Þ (a+a*F, aaF*+)
Þ (a+a*a, aaa*+).
Каждая выходная цепочка этой последовательности получается из предыдущей выходной цепочки заменой подходящего нетерминала правой частью элемента перевода, присоединенного к правилу, примененному при выводе соответствующей входной цепочки.
Перевод инфиксной формы записи в польскую
Схема перевода, рассмотренная выше, является сугубо "прологовской" и с практической точки зрения она малопригодна в силу крайне малой эффективности - основная проблема заключается в необходимости перебора возможных вариантов применения правил.
Для практических нужд более эффективным является следующий метод. Основная идея остается прежней - применение каждого правила грамматики влечет выполнение некоторых действий. Эти действия мы будем называть семантическими программами или процедурами.
Пусть задана следующая грамматика арифметического выражения (обратите внимание на то, что она является более расширенной по сравнению с предыдущими вариантами. Здесь появился даже унарный минус !)
Z ::= E
E ::= T | E+T | E-T | -T
T ::= F | T*F | T/F
F ::= a | (E)
Запишем схему перевода в следующем виде:
|
№ |
Правило |
Семантическая программа |
|
1 |
Z ::= E |
нет (*) |
|
2 |
E ::= T |
нет (**) |
|
3 |
E ::= E+T |
Push('+') (**) |
|
4 |
E ::= E-T |
Push('-') (**) |
|
5 |
E ::= -T |
Push('@') |
|
6 |
T ::= F |
Нет |
|
7 |
T ::= T*F |
Push('*') |
|
8 |
T ::= T/F |
Push('/') |
|
9 |
F ::= a |
Push(a) |
|
10 |
F ::= (E) |
Нет |
Это - явно более приближенный к практическому воплощению вариант. Здесь семантическая процедура Push(X) добавляет в конец выходной цепочки символ X. При этом надо сделать следующие замечания:
Правило (1) применимо, если R=# (символ # означает конец анализируемой последовательности); правила (2), (3), (4) применимы, если в R содержится '+', '-', '#' или ')'.
Итак, для того, чтобы реализовать алгоритм разбора без полного перебора возможных вариантов применимости правил, нам потребуется стек S и переменная R, которая будет хранить очередной считываемый символ.
Алгоритм СУ-перевода выглядит так: сначала в стек S заносится символ #. Далее к содержимому стека мы пробуем применить какое-либо правило из списка. Если ни одно из правил не срабатывает, то в стек заносится очередной символ анализируемой входной последовательности.
Проще всего изобразить процедуру разбора на конкретном примере, а сам процесс изобразить в виде некоторой таблицы (в столбце wk... мы будем записывать остаток входной цепочки символов). Рассмотрим разбор выражения "a*(b+c)#":
|
Стек S |
R |
wk... |
Номер правила |
Польская цепочка |
|
# |
a |
*(b+c)# |
|
|
|
#a |
* |
(b+c)# |
9 |
a |
|
#F |
* |
(b+c)# |
6 |
a |
|
#T |
* |
(b+c)# |
|
a |
|
#T* |
( |
b+c)# |
|
a |
|
#T*( |
b |
+c)# |
|
a |
|
#T*(b |
+ |
c)# |
9 |
ab |
|
#T*(F |
+ |
c)# |
6 |
ab |
|
#T*(T |
+ |
c)# |
2 |
ab |
|
#T*(E |
+ |
c)# |
|
ab |
|
#T*(E+ |
c |
)# |
|
ab |
|
#T*(E+c |
) |
# |
9 |
abc |
|
#T*(E+F |
) |
# |
6 |
abc |
|
#T*(E+T |
) |
# |
3 |
abc+ |
|
#T*(E |
) |
# |
|
abc+ |
|
#T*(E) |
# |
|
10 |
abc+ |
|
#T*F |
# |
|
7 |
abc+* |
|
#T |
# |
|
2 |
abc+* |
|
#E |
# |
|
1 |
abc+* |
|
#Z |
# |
|
STOP |
abc+* |
Признак нормального окончания работы алгоритма: когда в стеке остался единственный символ Z, а текущим символом является '#'- символ конца входной последовательности, то мы считаем, что процедура синтаксического анализа завершена успешно. В противном случае (если в стеке есть другие символы) фраза построена неверно.
Основной недостаток синтаксически-управляемого перевода (как, впрочем, и всех механизмов, основанных на применении грамматик в явном виде) заключается в том, что фактически мы имеем дело с полным перебором всех возможных вариантов применений правил грамматики. Избежать этого перебора позволяют лишь введенные весьма искусственные соглашения относительно условий применимости тех или иных правил в различных ситуациях (см. те же правила (1), (2), (3) и (4)). Более того, поиск как таковой и в схеме СУ-перевода, и в МП-автоматах, о которых мы будем говорить ниже, категорически недопустим. Вот если бы мы работали с Прологом, то тогда нам не пришлось бы вводить эти правила-ограничители поиска - внутренний механизм Пролога сам перебрал бы все возможные варианты применения правил. Здесь же нам нужно "стопроцентное" попадание в нужное правило.
Мы уже говорили о том, что теория конечных автоматов пригодна только для регулярных грамматик. Для контекстно-свободной грамматики вида
G = { {a , +, * , /, - , . , ) , ( } , {E, T, F,}P, E }
P = { ERT, ERE + T, ERE - T,
TRF, TRT*F, TRT/ F,
FRa, FR (E) }
создать конечный распознающий автомат уже невозможно.
Для этого существуют более сложные по своей структуре автоматы - автоматы с магазинной памятью, которые применяются для распознавания фраз контекстно-свободных грамматик.
Определение. Автомат с магазинной памятью (МП-автомат или стековый автомат) - это семерка
МП = (å, Q, Г, q0, z0, T, P), где
· å - конечный входной алфавит (входной словарь);
· Q - конечное множество состояний;
· Г - конечный алфавит магазинных символов;
· q0 - начальное состояние управляющего устройства (q0ÎQ);
· z0 - символ, находящийся в магазине в начальный момент времени (начальный символ), z 0ÎГ;
· T - множество терминальных (заключительных) состояний, TÌQ;
· P - отображение множества Q´(åÈ{e})´Г в множество конечных подмножеств множества Q´Г*.
P: Q´(åÈ{e})´Г R Q´Г*
Условно МП-автомат можно изобразить так:
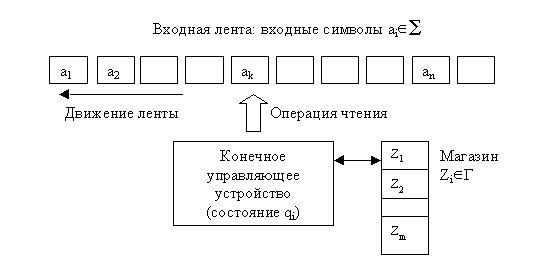
Конфигурацией МП-автомата называется тройка (q,w,a)ÎQ´å*´Г*, где
· q - текущее состояние устройства;
· w - неиспользованная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;
· a - содержимое магазина; самый левый символ цепочки a считается верхним символом магазина; если a=e, то магазин считается пустым.
Такт работы МП-автомата
(q,aw,Za)R (q', w,ga)
Если a=e, то этот такт называется e-тактом. В e-такте входной символ не принимается во внимание и входная головка не сдвигается. Если g=e, то верхний символ удаляется из магазина (магазинный список сокращается).
Начальная конфигурация МП-автомата - это тройка
(q0, w, Z0), wÎå*
Говорят, что цепочка w допускается МП-автоматом, если
(q0, w, Z0) R*(q, e, a) для некоторых qÎT и aÎГ*
На практике более полезным и универсальным является т.н. расширенный МП-автомат
МПr = (å, Q, Г, q0, Z0, T, Pr), где
Pr - отображение множества Q´(åÈ{e})´Г* в множество конечных подмножеств множества Q´Г*, а все остальные символы имеют тот же смысл, что и в определении МП-автомата.
В отличие от МП-автомата расширенный МП-автомат обладает способностью продолжать работу и тогда, когда магазин пуст.
Теорема. Пусть G = (N,å,P,S) - КС-грамматика. По грамматике G можно построить такой МП-автомат R, что Le(R)=L(G).
В качестве примера рассмотрим расширенный МП-автомат R, распознающий грамматику G0
G0=({E,T,F},{a,+,*,(,),#},P,E)
P = { E R E+T|T
T R T*F|F
F R (E)|a}
Здесь # - символ конца входной последовательности.
Определим автомат следующим образом:
R = (å,Q,Г,q0,Z0,T,P), где
Q = {q,r},
Г={E, T, F, $} È å
q0 = q,
Z0 = $,
T = {r},
P:
(1) (q,e,E+T) R (q,E) (*)
(2) (q,e,T) R (q,E) (*)
(3) (q,e,T*F) R (q,T)
(4) (q,e,F) R (q,T)
(5) (q,e,(E)) R (q,F)
(6) (q,e,a) R (q,F)
(7) (q,#,$E) R (r,e)
(8) (q,b,e) R (q,b) для всех bÎ{a,+,*,(,)};
Замечание 1. Правила, отмеченные (*), применимы, если следующим символом входной цепочки является '+', или '-', ')' или входная цепочка пуста.
Замечание 2. Приоритет выполнения правил определяется содержимым стека.
Пусть на входе распознавателя цепочка "a+a*a". Тогда процесс ее распознавания будет выглядеть так:
(q,a+a*a#,$) R (q, +a*a#, $a)
R (q, +a*a#, $F)
R (q, +a*a#, $T)
R (q, +a*a#, $E)
R (q, a*a#, $E+)
R (q, *a#, $E+a)
R (q, *a#, $E+F)
R (q, *a#, $E+T)
R (q, a#, $E+T*)
R (q, e, $E+T*a)
R (q, e, $E+T*F)
R (q, e, $E+T)
R (q, #, $E)
R (r, #, e)
Следует четко осознавать, что схема СУ-перевода и разбор КС-грамматики с помощью МП-автомата являются эквивалентными. В частности, если мы дополним МП-автомат набором семантических процедур, то МП-автомат, помимо синтаксического разбора, будет уметь формировать и польскую форму записи анализируемой фразы.
Более того, МП-автомат можно считать просто более формальным изложением алгоритма СУ-перевода. Например, алгоритм в СУ-перевода гласит: если ни одно из правил не применимо к содержимому стека, то следует поместить в стек очередной символ входной последовательности. В МП-автомате вместо этого используется правило (8). А условие завершения СУ-перевода формулируется правилом (7). Более того, если говорить о конкретной программной реализации обоих методов, то и в том, и в другом случае нам придется пользоваться практически эквивалентными структурами.
По-прежнему наша цель - решить задачу анализа входной последовательности и обойтись при этом как можно меньшими затратами на поиск. Метод, о котором пойдет речь далее, основан на понятии приоритета символов анализируемой последовательности.
Пусть дана входная цепочка символов ":.RS:". Попробуем сразу определить, какое правило нам будет удобнее выполнить (точнее, над какой частью цепочки сначала производить операции, т.е. с какого символа начинать). Для этого можно использовать понятие приоритета, основываясь на введенной системе отношений между символами, а именно:
для любой цепочки ":.RS:" возможны следующие варианты:
1) Если есть правило, заканчивающееся на R,
UR:R ,
тогда можно сказать, что R > S.
2) Если есть правило, включающее в себя RS,
UR:RS: ,
тогда можно сказать, что R = S.
3) Если же есть правило, начинающееся на S,
URS: ,
тогда можно сказать, что R < S.
Итак, существуют три варианта отношений между символами:
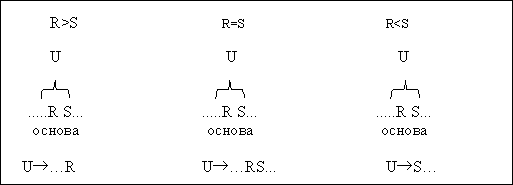
Здесь предполагается, что S - терминал
Алгоритм разбора
Нам потребуются два стека: стек операторов OP и стек аргументов ARG. Обозначим через S верхний символ в стеке операторов OP, а через R - входной символ.
Далее циклически выполняем следующие действия:
(1) Если R - идентификатор, то поместить его в ARG и пропустить шаги 2,3.
(2) Если f(S)<g(R), то поместить R в OP и взять следующий символ.
(3) Если f(S)³g(R), то вызвать семантическую процедуру, определяемую символом S. Эта процедура выполняет семантическую обработку, например, исключает из ARG связанные с S аргументы и заносит в ARG результат операции. Это - т.н. редукция сентенциальной формы.
Построим матрицу, строки которой будут соответствовать f(S), а столбцы - g(R). Для грамматики
ERE+T | T
TRT*F | F
FR(E) | i
эта матрица будет выглядеть следующим образом:
g(R)
|
|
|
+ |
* |
( |
) |
# |
|
|
+ |
> |
< |
< |
> |
< |
|
Стек |
* |
> |
> |
< |
> |
< |
|
F(S) |
( |
< |
< |
< |
= |
< |
|
|
) |
> |
> |
X |
> |
< |
|
|
# |
< |
< |
< |
< |
> |
Строки и столбцы # отвечают за ситуацию, когда входная последовательность пуста (и мы должны выполнить то, что осталось в стеке OP), и за начало работы, когда стек пуст и мы должны занести в очередной OP символ.
Элементы матрицы 'X' обозначают ошибочную (запрещенную) ситуацию.
Условием нормального окончания работы алгоритма является ситуация, когда в стеке находится единственный символ # (S=#), а значение R есть также #. Во всех остальных случаях считается, что разбираемое выражение построено некорректно.
Рассмотрим пример разбора выражения (a*b/c+d)*e#
|
S |
R |
w |
Arg |
f(S)?g(R) |
|
# |
|
(a*b/c+d)*e# |
|
|
|
# |
( |
a*b/c+d)*e# |
|
< |
|
#( |
a |
*b/c+d)*e# |
A |
< |
|
#( |
* |
b/c+d)*e# |
A |
< |
|
#(* |
b |
/c+d)*e# |
a, b |
< |
|
#(* |
/ |
c+d)*e# |
a, b |
> |
|
#( |
/ |
c+d)*e# |
(a*b) |
< |
|
#(/ |
c |
+d)*e# |
(a*b), c |
< |
|
#(/ |
+ |
d)*e# |
(a*b), c |
> |
|
#( |
+ |
d)*e# |
((a*b)/c) |
< |
|
#(+ |
d |
)*e# |
((a*b)/c), d |
< |
|
#(+ |
) |
*e# |
((a*b)/c), d |
> |
|
#( |
) |
*e# |
(((a*b)/c)+d) |
= |
|
# |
* |
e# |
(((a*b)/c)+d) |
< |
|
#* |
e |
# |
(((a*b/)c)+d), e |
< |
|
#* |
# |
|
(((a*b)/c)+d), e |
> |
|
# |
# |
|
((((a*b/)c)+d)*e) |
> |
Достоинством данного метода является его несомненная простота, а также высокая скорость выполнения (не тратится время на поиск правила редукции). Более того, этот метод может быть применен не только для разбора арифметических выражений, но и для анализа фраз контекстно-свободных языков вообще.
Однако все эти достоинства напрочь меркнут перед главным недостатком данного метода. Дело в том, что здесь практически отсутствует какая бы то ни была диагностика (и тем более - локализация) ошибок (кроме случая обращения к элементу матрицы X). Во вторых, некоторые ошибки в исходном выражении не диагностируются вовсе. Например, выражения, в которых встречаются идущие подряд скобки <(> и <)>.
И последнее замечание. Основная наша цель заключалась в формировании некоторой промежуточной формы представления исходной программы. Здесь же происходит непосредственное вычисление выражения. Тем не менее, этот метод пригоден и для формирования как польской формы записи, так и тетрад. Формирование необходимых выходных последовательностей происходит в момент редукции, т.е. в момент вызова процедуры семантической обработки. Например, с стек ARG можно просто помещать последовательно не только операнды, но и операторы, взятые из стека S. Тогда в ARG мы получим польскую форму записи разбираемого выражения.
Перейдем теперь от анализа арифметических выражений к более сложным объектам - программам. Пусть у нас есть язык, включающий в себя оператор присваивания, а также условный и циклический операторы. Грамматика такого языка в самом упрощенном виде может выглядеть так:
прогр ::= инстр
инстр ::= инстр; инстр
инстр ::= перем := выр
инстр ::= if выр then инстр else инстр end
инстр ::= while выр do инстр end
выр ::= выр +перем | перем
перем ::= i
Тогда мы сможем писать программы наподобие следующей:
d := 10;
a := b+c-d;
if a then d := 1 else
while d do
e := e-1
end
end
Как видно, язык этот, несмотря на свою простоту, позволяет создавать весьма нетривиальные условные и циклические конструкции.
Описанные выше способы анализа предложений КС-языков имеют существенный недостаток, связанный с необходимостью реализации процедуры поиска правил или просмотра таблицы для выбора нужной редукции.
Далее мы рассмотрим еще один метод анализа подобного рода языков. Это - весьма старый метод, разработанный еще на заре становления теории компиляторов, однако он хорошо зарекомендовал себя и используется в практически неизменном виде и поныне. Этот метод основан на использовании т.н. таблицы решений или матрицы переходов.
Для наглядности рассмотрим еще более упрощенный вариант грамматики нашего языка:
<прог> ::= <инстр>
<инстр> ::= IF <выр> THEN <инстр>
<инстр> ::= <перем> := <выр>
<выр> ::= <выр> + <перем> | <перем>
<перем> ::= i
Для реализации матрицы переходов нам, как всегда, понадобится стек, переменная, хранящая текущий считываемый символ, и переменная, в которой будет храниться значение последней приведенной формы.
Стек необходим нам для хранения правых частей грамматики, заканчивающихся терминалом. Эта часть называется головой правила.
Строки матрицы переходов соответствуют тем головам правых частей правил, которые могут появиться в стеке, а столбцы соотносятся с терминальными символами, включая и ограничитель предложений #. Элементами матрицы будут номера или адреса подпрограмм.
|
|
# |
IF |
THEN |
:= |
+ |
i |
|
# |
5 |
1 |
0 |
6 |
0 |
1 |
|
IF |
0 |
0 |
9 |
0 |
3 |
1 |
|
IF <выр> THEN |
7 |
1 |
0 |
6 |
0 |
1 |
|
<перем> := |
8 |
0 |
0 |
0 |
3 |
1 |
|
<выр> + |
4 |
0 |
4 |
0 |
4 |
1 |
|
i |
2 |
0 |
2 |
2 |
2 |
0 |
Итак, распознаватель использует стек S, переменную R, принимающую значение текущего считываемого символа, а также переменную U, которая либо пуста, либо содержит тот символ, к которому была приведена последняя первичная фраза (иными словами, значением переменной является последняя разобранная синтаксическая категория).
Структура стека несколько отличается от предыдущих: элементами стека являются не отдельные символы, а цепочки символов - головы правых частей правил. Например, последовательность
# IF <выр> THEN IF <выр> THEN <перем> :=
в стеке будет представлена следующим образом:
|
|
|
<перем> := |
|
IF <выр> THEN |
|
IF <выр> THEN |
|
# |
Итак, в стеке хранятся те последовательности символов, которые должны редуцироваться одновременно.
Распознаватель работает следующим образом. На каждом шаге работы верхний элемент стека соответствует некоторой строке матрицы. По входному терминальному символу (это - столбец) определяется элемент матрицы, являющийся номером подпрограммы, которую нужно выполнить. Эта подпрограмма произведет необходимую редукцию или занесет R в стек и будет сканировать следующий исходный символ. При написании подпрограмм будем считать, что функция PUSH(R) помещает в стек символ R, функция SCAN() помещает очередной символ из входной цепочки в R, а функция POP() просто извлекает из стека верхний символ (предполагается, что он нам уже не нужен).
Схема рассуждений при формировании подпрограмм выглядит так (рассмотрим, для примера, подпрограмму 9): сначала мы выписываем содержимое верхнего элемента стека (для нашей подпрограммы это будет IF). Далее записываем значение считанного терминала (это THEN) и смотрим, что может находиться между ними (т.е. какая синтаксическая категория U):
:IF U THEN:
Судя по всему, U должно быть равно <выр>. Значит, первая процедура нашей подпрограммы - это проверка вида
if U¹<выр> then error()
Затем смотрим, не получилось ли у нас разобранной синтаксической категории. Ничего путного пока у нас не вышло, поэтому присвоим переменной U пустое значение (U := ''), а в стек занесем полученную голову правила (PUSH('IF <выр> THEN')). Далее надо будет считать следующий входной символ. Итак, подпрограмма номер 9 будет выглядеть так:
9: IF U¹'<выр>' AND U¹'<перем>' THEN ERROR();
PUSH('IF <выр> THEN')
U := '';
SCAN().
Еще пример. В самом начале в стеке находится символ # и U пусто. В соответствии с нашей грамматикой входным символом должен быть либо IF, либо i. Поскольку с них начинаются правые части, необходимо занести их в стек и продолжить работу. Тогда первой подпрограммой будет такая:
1: IF U¹ '' THEN ERROR(); PUSH(R); SCAN().
Предположим, что i - верхний элемент стека. Определим теперь, какие символы из тех, которые могут оказаться в R, считаются допустимыми. За i могут следовать символы: #, THEN, := или +. В любом из этих случаев необходимо заменить i на <перем>, т.е. выполнить редукцию
...<перем>... => ...i...
В подпрограмме 2 именно это и делается:
2: IF U¹'' THEN ERROR(); POP(); U := '<перем>'
Итак, каждый элемент матрицы является номером подпрограммы, которая либо заносит входной символ в стек, либо выполняет редукцию.
Приведем все подпрограммы, соответствующие нашей матрице переходов:
(1) IF U¹'' THEN ERROR(1);
PUSH(R);
SCAN().
(2) IF U¹'' THEN ERROR(2);
POP();
U := '<перем>'.
(3) IF U¹'<выр>' AND U¹'<перем>' THEN ERROR(3);
PUSH('<выр>+')
U := '';
SCAN().
(4) IF U¹'<перем>' THEN ERROR(4);
POP();
U := '<выр>'.
(5) IF U¹'<прог>' AND U¹'<инстр>' THEN ERROR(5);
STOP().
(6) IF U¹'<перем>' THEN ERROR(6);
PUSH('<перем>:=')
U := '';
SCAN().
(7) IF U¹'<инстр>' THEN ERROR(7);
POP();
U := '<инстр>'.
(8) IF U¹'<выр>' AND U¹'<перем>' THEN ERROR(8);
POP();
U := '<инстр>'.
(9) IF U¹'<выр>' AND U¹'<перем>' THEN ERROR(9);
PUSH('IF <выр> THEN')
U := '';
SCAN().
(0) ERROR(10);
STOP().
На самом деле мы поступили не совсем корректно, определяя подпрограммы с одинаковыми номерами. Все подпрограммы должны быть уникальными. Дело в том, что каждая подпрограмма выдает свою собственную диагностику ошибок. А это очень важный фактор.
То, чем мы занимались до сих пор, касалось лишь задачи анализа. А как же быть с синтезом (например, польской формы)? Процедура синтеза осуществляется тогда, когда происходит редукция формы, т.е. тогда, когда срабатывает какое-либо правило грамматики и переменная U получает значение. К этому моменту нам известно, какие инструкции подлежат редукции и обработке.
Способ матриц переходов - это очень быстрый метод обработки, т.к. в нем полностью исключается поиск. Во-вторых, очень эффективна нейтрализация ошибок: каждый нуль в матрице соответствует определенной синтаксической ошибке. Так как нулей, соответствующих частным случаям ошибок, в матрице обычно много, то диагностика получается достаточно полной. По меньшей мере, метод матриц переходов - это наиболее эффективный с точки зрения нейтрализации ошибок способ обработки. Кроме того, матрица переходов достаточно легко может быть отредактирована и/или дополнена новыми элементами по ходу развития представлений разработчика об устройстве создаваемого языка. Вдобавок ко всему, по имеющейся грамматике языка матрица переходов может быть сформирована автоматически.
Недостаток метода матрицы переходов заключается в том, что для более сложной грамматики получается матрица очень большого размера, что влечет массу проблем особенно в том случае, если мы пытаемся сформировать ее вручную.
На этом мы закончим рассмотрение методов синтаксического анализа. Разберемся теперь с тем, как могут быть представлены результаты этого анализа.
Мы уже говорили о том, что внутренняя форма - это промежуточная форма представления исходной программы, пригодная (1) для простой машинной обработки (операторы располагаются в том же порядке, в котором они и будут исполняться); (2) для интерпретации. Рассмотрим, как представимы во внутренней форме некоторые наиболее употребительные операторы. Начнем с польской формы.
Вернемся к вопросу вычисления польской формы записи. При этом модифицируем первоначальный алгоритм так, чтобы операнды выбирались не из входного потока непосредственно, а из специально отведенного для этого стека. Как и раньше, будем хранить в R текущий считываемый символ.
(1) Если R является идентификатором или константой, то его значение заносится в стек и осуществляется считывание следующего символа (правило "<операнд>::=идентификатор").
(2) Если R - бинарный оператор, то он применяется к двум верхним операндам в стеке, и затем они меняются на полученный результат (правило "<операнд>::=<операнд><операнд><оператор>").
(3) Если R - унарный оператор, то он применяется к верхнему символу в стеке, который затем заменяется на полученный результат (правило "<операнд>::=<операнд><оператор>").
Упрощенно алгоритм вычисления польской формы (ПФ) выглядит так:
R := getchar
while R != # do
case R of
'идентификатор': push(R)
'бин.оператор': pop(B), pop(A), Tmp := R(A,B), push(Tmp)
'унарн.оператор': pop(A), Tmp := R(A), push(Tmp)
endcase
R := getchar
endwhile
Обычно, при выполнении оператора присваивания в стек мы ничего не заносим (это справедливо для "алголоподобных" языков, к которым, в частности, относится и Паскаль).
Польскую форму легко расширять. Рассмотрим включение в ПФ других, отличных от арифметических, операторов и конструкций. Символом $ мы будем предварять имена операторов, чтобы не спутать их с аргументами.
Безусловные переходы
Безусловный переход на метку (аналог GOTO L)
L $BRL (Branch to label)
L - имя в таблице символов. Значение его - адрес перехода. Основная проблема при реализации этого оператора - определение адреса перехода. Возможным решением является введение фиктивного оператора, соответствующего метке, на которую будет осуществлен переход с последующим поиском его в массиве польской формы.
Безусловный переход на символ
C $BR
Под символом здесь понимается номер позиции (индекс) в массиве, содержащем польскую форму.
Условные переходы
<операнд1> <операнд2> $BRxZ|$BRM|$BRP|$BRMZ|$BRPZ|
<операнд1> - значение арифметического выражения,
<операнд2> - номер или место символа в польской цепочке (адрес).
$BRx - код оператора. При этом можно ввести самые разнообразные условия перехода. Например:
$BRZ - переход по значению 0,
$BRM - переход по значению <0,
$BRP - переход по значению >0,
$BRMZ - переход по значению <=0,
$BRPZ - переход по значению >=0,
и т.п.
При выполнении условия перехода в качестве следующего символа берется тот символ, адрес которого определяется вторым операндом. В противном случае работа продолжается как обычно.
Условные конструкции
IF <выражение> THEN <инстр1> ELSE <инстр2>
В ПФ мы имеем:
<выражение> <c1> $BRZ <инстр1> <c2> $BR <инстр2>
Предполагается, что для любого выражения 0 означает "ложь", а неравенство нулю - "истина". Здесь
<c1> - номер символа, с которого начинается <инстр2>,
<c2> - номер символа, следующего за <инстр2>,
$BR - оператор безусловного перехода на символ,
$BRZ - оператор перехода на символ c1, если значение <выражение> равно нулю).

Обратите внимание на то, что при выполнении операторов перехода из стека лишь извлекается необходимое количество символов, а обратно ничего не возвращается.
Понятно, что применение ПФ для условной конструкции в виде
<выр> <инстр1> <инстр2> $IF
неприемлемо, ибо к моменту выполнения оператора $IF все три операнда должны быть уже вычислены или выполнены, что, разумеется, неверно.
Описание массивов
Пусть дано описание массива
ARRAY A[L1..U1,...,Lk..Uk]
в ПФ оно представляется в виде
L1 U1 ... Lk Uk A $ADEC,
где $ADEC - оператор объявления массива. Оператор $ADEC имеет переменное количество аргументов, зависящее от числа индексов. Операнд A - адрес в таблице символов. При вычислении $ADEC из этого элемента таблицы извлекается информация о размерности массива A и, следовательно, о количестве операндов $ADEC. Отсюда понятно, почему операнд A должен располагаться непосредственно перед оператором $ADEC.
Обращение к элементу массива и вызовы подпрограмм
Конструкция A[<выр>,..,<выр>] записывается в виде
<выр> .. <выр> A $SUBS
Оператор $SUBS, используя элемент A таблицы символов и индексные выражения, вычисляет адрес элемента массива. Затем операнды исключаются из стека и на их место заносится новый операнд, специфицирующий тип элемента массива и его адрес.
Методика обращения к элементу массива представляется очень важной для понимания того, как происходит вызов функций и процедур. Дело в том, что при обращении к функции нам также необходимо извлекать откуда-то необходимое количество аргументов. А количество их мы можем определить по содержимому таблицы имен. Поэтому вызов функции вида f(x1,x2) в польской форме записи будет выглядеть как
x1 x2 f $CALL,
где x1 и x1 - аргументы, f - имя функции, $CALL - команда передачи управления по адресу, определяемому именем функции. При этом предполагается, что мы заранее занесли в таблицу имен информацию о том, сколько и каких аргументов у функции f, а также ее адрес - индекс начала кода подпрограммы в массиве польской формы.
Не случайно поэтому, что в подавляющем количестве языков программирования имена функций ассоциируются с их адресами.
Циклы
Реализация циклов также не вызывает сложностей. Во-первых, имея оператор безусловного перехода и условный оператор, можно всегда сконструировать цикл "вручную". Например, цикл вида
FOR I=N1 TO N2 DO Operator
может быть сконструирован на исходном языке:
I := N1;
L1: IF I>N2 THEN GOTO L2;
Operator;
I:=I+1;
GOTO L1;
L2:
Тем не менее, если необходимо реализовать этот цикл как оператор языка, то в польской форме записи он будет выглядеть так:
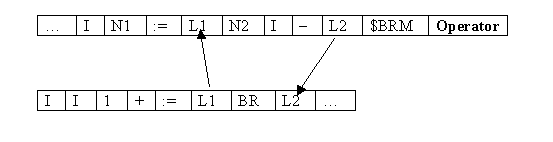
Рассмотрим фрагмент программы:
BEGIN
INTEGER K;
ARRAY A[1..I-J];
K := 0;
L: IF I>J THEN
K := K+A[I-J]*6
ELSE
BEGIN
I := I+1;
I := I+1;
GOTO L;
END
END.
Добавим еще два оператора без операндов - $BLOCK ("начало блока") и $BLOCKEND ("конец блока"). Эти операторы иногда очень важны - в некоторых языках программирования с их помощью можно вводить локальные, "внутриблоковые" переменные, вызывать автоматически деструкторы и т.п. Кроме того, нам понадобится оператор присваивания ":=", который ничего не заносит обратно в стек. Польская форма нашего фрагмента будет выглядеть так:

В заключение хотелось бы добавить одно замечание. Хранение оператора, ключевого слова и т.п. в массиве польской формы трудностей не вызывает - мы содержим там лишь числовой код (например, в виде отрицательного числа). Операнды тоже представлены числами - индексами таблицы имен, где хранятся и переменные, и константы.
Сложнее обстоит дело со стеком аргументов, необходимым для вычисления польской формы, и в котором хранятся значения рабочих, промежуточных переменных. Это могут быть и целые, и действительные числа, строки, символы, адреса и т.п. Следовательно, необходимо предусмотреть хранение, помимо собственно значения, и тип аргумента, и размер и, возможно, многое другое. На это следует обращать особое внимание при разработке компиляторов.
Одним из возможных вариантов организации рабочего стека является использование т.н. тегового стека. В теговом стеке каждый хранимый элемент предваряется неким описателем его типа, называемым тегом. Тег может содержать самую разнообразную информацию, описывающую данные - тип, размер, права доступа и т.д.
Для простейшего интерпретатора можно различать такие типы данных, как числовые, строковые и адресные. В качестве адреса в простейшем случае может использоваться целое число - номер записи в таблице имен.
Добавление тетрад с другими операторами также не вызывает трудностей и происходит аналогично. Тот же фрагмент программы, представленный в форме тетрад, выглядит так:
(1) $BLOCK (10) + K, T4, T5
(2) - I, J, T1 (11) := T5,, K
(3) $BOUNDS 1, T1 (12) $BR 18
(4) $ADEC A (13) + I, 1, T6
(5) := 0,, K (14) := T6,, I
(6) - I, J, T2 (15) + I, 1, T7
(7) $BMZ 13, T2 (16) := T7,, I
(8) - I, J, T3 (17) $BRL L
(9) * A[T3], 6, T4 (18) $BLOCKEND
Здесь используются следующие операторы:
|
Оператор |
Операнды |
Описание |
|
$BR |
i |
переход на i-ю тетраду |
|
$BZ (BP,BM) |
i, P |
переход на i-ю тетраду, если P=0 (P>0,P<0) |
|
$BG (BL,BE) |
i, P1, P2 |
переход на i-ю тетраду, если P1>P2 (P1<P2,P1=P2) |
|
$BRL |
P |
переход на тетраду, номер которой задан в P-м элементе таблицы символов |
|
$BOUNDS |
P1, P2 |
P1 и P2 описывают граничную пару массива |
|
$ADEC |
P |
Массив описан в P. Если размерность массива равна n, то этой тетраде должны предшествовать n операторов $BOUNDS, задающих n граничных пар |
С тетрадой номер 9 могут возникнуть определенные проблемы. Трудности связаны с использованием аргумента в виде переменной с индексом. Решение может заключаться в использовании той же методики, что и в случае описания массивов.
Введем пару операторов типа
$AINDX I
$AGET A, R
$AINDX заносит аргумент I (индекс массива) в специальный стек - стек индексов. Это необходимо для того, чтобы команда $AGET смогла вычислить адрес элемента массива A, используя содержимое стека индексов, и занести значение этого элемента в R. В этот же момент может происходить и очистка стека (по мере извлечения необходимого количества аргументов)
Например, выражение "A[1,2]+B[J]" будет представлено в виде
$AINDX 1
$AINDX 2
$AGET A, T1
$AINDX J
$AGET B, T2
+ T1, T2, T3
По такому же принципу может быть организован и вызов подпрограмм. Кстати, здесь особенно явно проявляется роль стека при обращении к подпрограммам. Иллюстрацией этому могут служить наверняка знакомые большинству программистов неприятности со стеком, когда неверно указывается количество или тип аргументов при вызове подпрограмм (особенно в языке С).
Оптимизация программ - это очень объемная тема, на которую написаны (и пишутся до сих пор) многочисленные труды. Здесь мы лишь вкратце затронем этот вопрос.
Различают два основных вида оптимизации - машинно-зависимую (МЗО) и машинно-независимую (МНЗО):
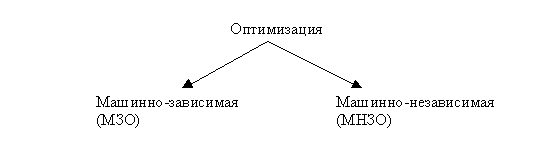
МЗО связана с типом генерируемых команд и включается в фазу генерации кода (т.е. оптимизации подлежат машинные коды). МЗО напрямую зависит от архитектуры вычислительной машины и потому рассматриваться нами не будет.
В отличие от МЗО, МНЗО - отдельная фаза компилятора, предшествующая генерации кода. Она включается на этапе генерации промежуточного кода - внутренней формы представления программы.
Оптимизации подлежат:
- время выполнения;
- емкостные ресурсы (память).
Существуют 4 основных типа машинно-независимой оптимизации МНЗО.
I. Исключение общих подвыражений (оптимизация линейных участков)
Оптимизация линейных участков - это процедура, позволяющая не рассчитывать одно и то же выражение несколько раз, исключая общие подвыражения. Эта процедура разделяется на следующие шаги:
- представить выражение в форме, пригодной для обнаружения общих подвыражений;
- определить эквивалентность двух и более подвыражений;
- исключить повторяющиеся;
- изменить команды так, чтобы учесть это исключение.
Например, пусть выражение A = c*d*(d*c+b) записано в виде тетрад:
(1) * c d T1
(2) * d c T2
(3) + T2 b T3
(4) * T1 T3 T4
(5) = A T4
Упорядочим операнды в алфавитном порядке (там, где это возможно):
(1) * c d T1
(2) * c d T2
(3) + T2 b T3
(4) * T1 T3 T4
(5) = A T4
Далее определим границы операторов и найдем общие подвыражения (это (1) и (2)) и затем исключим подвыражение (2). После чего заменим далее везде T2 на T1:
(1) * c d T1
(2) + T1 b T3
(3) * T1 T3 T4
(4) = A T4
Этот прием неудобен тем, что возможны варианты, когда либо не представляется возможным отыскать сразу общие выражения, либо в тех случаях, когда b, c, d - функции, имеющие побочный эффект; в этом случае мы можем поломать всю логику вычислений.
II. Вычисления на этапе компиляции
Если в программе есть участки, в которых присутствуют подвыражения, состоящие из констант, то эти подвыражения можно просчитать на этапе компиляции. Например, вполне возможно заранее вычислить правую часть выражения вида
A:= 1,5 * 2/3
III. Оптимизация булевых выражений
Метод основан на использовании свойств булевых выражений. Например, вместо
if (a and b and c) then <операторы> endif
надо сгенерировать команды таким образом, чтобы исключались лишние проверки. Суть метода состоит в том, что мы строим разветвление условия оператора if. Таким образом, вместо "if (a and b and c) then <операторы> endif" получим:
if not a then goto Label
if not b then goto Label
if not c then goto Label
<операторы>
Label: //метка перехода
Проблемы, связанные с использованием этого метода, заключаются в том, что, во-первых, могут проявиться побочные эффекты в тех случаях, когда аргументами являются функции, а во-вторых, "оптимизированный" код может получиться более громоздким по сравнению с оригиналом.
IV. Вынесение инвариантных вычислений за пределы цикла
Это - один из наиболее эффективных методов оптимизации, дающий весьма ощутимые результаты.

Для реализации метода необходимо:
- распознать инвариант;
- определить место переноса;
- перенести инвариант.
Неудобства метода:
- отследить инвариант нелегко, т.к. аргументы могут косвенно зависеть от переменной цикла;
- не учитываются побочные эффекты, если аргументы инварианта являются функциями (или зависимыми от них).
Проблемы, связанные с оптимизацией
Итак, очевидно, что необходимо сопоставлять ожидаемый выигрыш от повышения эффективности объектной программы с дополнительными накладными расходами, связанными с увеличением времени компиляции, надежности и сложности самого компилятора. Во-вторых, с оптимизаций зачастую связаны такие "неприятности", как даже ухудшение кода, сложность трассировки оптимизированных программ. Кроме того, бывает очень сложно выявить и/или устранить возникающие "побочные" эффекты.
Например, пусть мы работаем со стеком, используя функции push() для записи числа в стек и pop() для извлечения числа. Если нам надо извлечь пару чисел из стека и поместить обратно в стек их логическую сумму, то мы можем написать что-то вроде
A := pop();
B := pop();
C := A || B;
Push(C);
Причем этот вариант является обычно более предпочтительным перед компактным вида
Push(pop() || pop()),
ибо скорее всего оптимизирующий компилятор превратит это выражение в Push(pop()), сочтя второй pop() лишним (он честно будет использовать логическую парадигму A || A º A). Это типичный пример побочных эффектов оптимизации.
Выводы
1. Необходимо сопоставлять затраты на оптимизацию с ожидаемым эффектом.
2. Оптимизация не всегда приводит к улучшению кода - могут появиться побочные эффекты. Либо после оптимизации получается более громоздкий код.
3. Чем больше вычислительной работы перекладывается на этап компиляции, тем эффективнее будет выполняться программа.
4. Более предпочтительной для МНЗО является внутренняя форма представления программы в виде тетрад.
5. Лучший прием оптимизации - писать хорошие программы.
По большому счету все то, что изучалось выше, предназначалось для того, чтобы дать необходимый теоретический базис и практические навыки и приемы, необходимые для построения интерпретатора - простейшего в ряду транслятор-компилятор-интерпретатор. Итак, мы уже знаем, что интерпретатор - это программа, которая
- транслирует исходную программу на языке высокого уровня во внутреннее представление;
- выполняет (интерпретирует) программу, представленную на этом внутреннем языке.
Интерпретатор прост. Его логическая структура напоминает урезанный компилятор. Интерпретаторы хороши для обучения (когда большая часть времени уходит на отладку) и для тех языков, в которых много времени уходит на работу системных программ (работа с матрицами, базами данных и т.п.).
Достоинства интерпретаторов
- простота (не надо реализовывать генерацию объектного кода);
- удобство и простота отладки программ - все внутренние структуры нам доступны (прежде всего - это доступ к таблице символов в любой момент времени), легки трассировка, отслеживание обращений к меткам и переменным (например, при установке флага проверки обращения в той же таблице символов) и т.п.;
- возможность включения интерпретируемых выражений в процессе выполнения программы (самомодификация программы).
Именно поэтому интерпретаторы наиболее часто применяются при разработке новых (не случайно сначала был создан именно интерпретатор языка С) и сложных языков - скажем, Пролог и Смолток в классическом варианте являются интерпретируемыми языками.
Недостатки интерпретаторов
Основным недостатком интерпретатора является малая, "по определению", скорость выполнения программы, т.к. при запуске нам необходимо выполнить все фазы анализа. Для устранения этого недостатка приходится платить упрощением синтаксиса языка, т.е. его грамматики. (Львиная доля времени работы интерпретатора приходится на анализ - лексический и синтаксический). В связи с этим наиболее простыми для реализации являются языки командного типа. В таких языках каждое предложение - это команда (императив) вида "<команда> [<аргументы>]".
Наиболее эффективной формой внутреннего представления программы для интерпретатора является польская форма записи. Тогда основной частью интерпретатора является переключатель CASE:
while TRUE do
begin
case gettype(P[n]) of
operand: Push(S,P[n]);
operator: arg1 := Pop(); arg2 := Pop(); Push(arg1 @ arg2);
else: error();
endcase
n := n+1
end
Выше уже говорилось о том, что при реализации интерпретатора возникает проблема представления в стеке аргументов различных типов данных. На практике существуют 4 типа аргументов:
- константы,
- имена,
- адреса переменных (адрес значения, номер элемента таблицы),
- указатели (поле "Значение" содержит номер (адрес) элемента в таблице символов).
Зачастую между этими понятиями существует некоторая путаница. Обычно это касается понятий адреса и указателя. Для наглядности их можно изобразить на следующем рисунке:
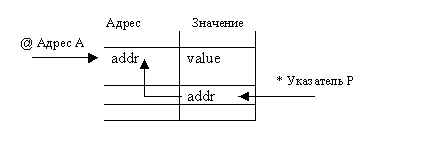
Существуют два основных способа хранения типа операнда (напомним, что в массиве польской формы записи операнды представляют собой положительные числа - адреса элементов в таблице имен). Во-первых, различать типы данных можно, используя аналогию с байт-кодом. Либо можно хранить аргумент, предваряя его элементом, указывающим тип (о теговом стеке говорилось выше). Во-вторых, тип элемента можно держать в таблице имен, и тогда в польской форме мы будем хранить лишь адреса. Если первый метод обеспечивает максимальное быстродействие (можно сразу определить тип аргумента, не обращаясь к таблице имен), то второй способ хранения более компактен. Как всегда, за все надо платить. Тем не менее, второй способ является более предпочтительным - он "красивее" и естественней.
Кроме того, очевидна необходимость наличия механизма проверки типов и соответствующих функций конвертирования. Вроде следующих:
cvPV (pointer to value) - конвертация указателя в значение;
cvPA (pointer to address) - конвертация указателя в адрес;
cvAV (address to value) - конвертация адреса в значение.
Для увеличения эффективности выполнения программы можно заранее вставлять в польскую форму записи процедуры конверсии типов (напомним основной принцип - не оставлять на время выполнения программы то, что можно сделать на этапе компиляции).
И последние замечания по поводу возможной реализации интерпретатора.
Трассировка. Можно легко и просто включить режим трассировки значений переменных. Например, установить флаг в таблице переменных и в соответствии с ним выводить значение переменной при обращении к ней по чтению и/или записи. Аналогично можно поступать и с метками, и с подпрограммами.
Для диагностики ошибок можно вставлять в польскую форму записи нумерацию строк исходной программы - некоторые фиктивные операторы, нужные только для отладки.
При реализации языка, в котором существуют подпрограммы, необходимо четко представлять себе механизм их вызова. Хороший сканер поместит в таблицу имен не только имя самой подпрограммы, но и ее тип, и количество и типы аргументов. Эта информация нужна будет для того, чтобы, выполняя оператор передачи управления $CALL, система взяла бы из стека необходимое количество операндов и могла бы поместить обратно значение, возвращаемое функцией. Кроме того, следует помнить и о локальных переменных, определенных внутри подпрограммы. Наиболее приемлемым способом избавиться от "засорения" таблицы имен локальными переменными является помещение их в стек. Тогда естественным образом будет решена и проблема их видимости.
Обычно интерпретатор - это самостоятельная программа, что зачастую создает некоторые проблемы, связанные с мобильностью программного обеспечения (в том смысле, что один исполняемый файл удобнее пары - исходный текст программы плюс интерпретатор). Однако существуют т.н. "скрытые" или "неявные" интерпретаторы. Реализация неявного интерпретатора заключается в том, что формируется исполняемый файл, содержащий в себе как непосредственно интерпретатор, так и исходный текст программы (почти в явном виде). Это приводит к тому, что внешне мы имеем исполняемый модуль, который, однако, занимается не чем иным, как интерпретацией со всеми вытекающими отсюда последствиями - достоинствами и недостатками. Типичным примером подобных систем является старая система программирования Clipper.
Пишутся интерпретаторы обычно на языках высокого уровня. И особенно полезными являются здесь принципы объектно-ориентированного программирования. Однако зачастую эффективнее бывает технология, при которой сначала создается макетный интерпретатор, реализованный, скажем, на Прологе. Макетный интерпретатор является полигоном для отладки структуры языка, он, естественно, прост, но малоэффективен с точки зрения скорости интерпретации. Однако для отладки структуры языка Пролог - незаменимое средство. Интерпретатор языка, среднего между Бейсиком и Паскалем, можно написать за 2-3 дня, и занимать он будет 400-500 строк (личный рекорд автора - это интерпретатор языка, в котором есть циклы, условные операторы, операторные скобки и полная арифметика с набором математических функций, который был написан за два вечера и занимал чуть более 400 строк). После отладки структуры языка можно браться за реализацию интерпретатора и на более эффективных с вычислительной точки зрения языках.
Выше мы уже упоминали о компиляторах компиляторов (КК) - системах, позволяющих создавать компиляторы. На самом деле КК - это некий инструментарий программиста, помогающий создавать компиляторы (или интерпретаторы). Создавая множество компиляторов или постоянно модифицируя грамматику разрабатываемого языка (к сожалению, далеко не всегда можно заранее ясно определить структуру и синтаксис), разработчик, естественно, желает некоторым образом автоматизировать некие рутинные процедуры. Не случайно все рассмотренные нами методы анализа по возможности представлялись в формальном виде. Все они могли быть автоматизированы. Имея регулярную грамматику лексической структуры можно, автоматически сгенерировать сканер в виде конечного автомата. Имея грамматику синтаксической структуры, можно написать универсальную процедуру синтаксически управляемого перевода (или создать универсальный МП-автомат).
Следовательно, по крайней мере эти две наименее творческие и наиболее сложные и рутинные составляющие компилятора можно сгенерировать автоматически.
Для этого потребуется некоторое описание двух наших грамматик - грамматики для сканера и грамматики для реализации синтаксического анализатора. Это описание вполне можно хранить в некотором файле. И тогда мы получим своего рода специальный входной язык - язык описания компилятора.
Разумеется, получить на выходе готовый компилятор мы не сможем. В лучшем случае на выходе будут некоторые фрагменты компилятора:
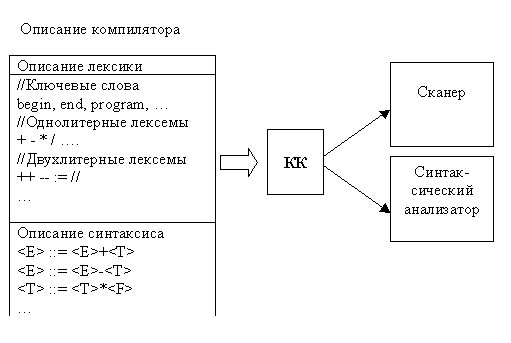
А дальше разработчику все равно необходимо будет самостоятельно добавлять семантические процедуры. С семантикой без него все равно ни один КК не справится. И еще пара замечаний.
Во-первых, при описании синтаксиса желательно правила грамматики записывать как можно в более естественной форме, при этом отделяя синтаксические категории от терминальных символов (скажем, заключая синтаксические категории в угловые скобки). С одной стороны, это сделает описание более удобочитаемым, а с другой - позволит КК легко разделять символы обоих словарей (терминального и нетерминального).
Во-вторых, нельзя забывать про наличие в схеме СУ-перевода (если КК реализует именно этот метод) еще двух составляющих - условия применимости правила грамматики и семантической процедуры. Все это тоже должно быть описано. Если описать семантическую процедуру достаточно просто, то с условием применения все гораздо сложнее. Ведь условие, в общем случае, может быть представлено произвольным логическим выражением. Дабы не заниматься его анализом с последующим вычислением, можно посоветовать сразу записывать это выражение в польской форме. Получится хоть не совсем красиво, зато удобно и очень просто.
И последнее. Познакомиться с описанием одного из наиболее почтенных КК можно в замечательной книге Кернигана и Пайка (см.библиографию). Описанный там КК YACC (Yet Another C compiler - еще один компилятор С или Yet Another compiler compiler - еще один компилятор компиляторов) представляет весьма мощный инструмент, хотя использование его - занятие весьма утомительное. На самом же деле пользоваться надо своим собственным инструментарием. КК - это один из немногих продуктов, ценность которого определяется его "эксклюзивностью".
Перед нами стоит одна из наиболее сложных задач изучаемого курса - познакомиться с совершенно новым и необычным языком программирования - языком Пролог. Этот язык интересует нас с точки зрения его применимости для построения важнейшей части любого компилятора - синтаксического анализатора. Как мы убедимся далее, Пролог для этой цели подходит более всех других языков.
Пролог - это достаточно "древний" язык. Он был создан в 1973 Алэном Колмеро во Франции, в Марсельском университете. Особенно популярен Пролог в Европе и в Японии. В 1981 г., анонсируя проект создания ЭВМ пятого поколения, японцы выбрали именно Пролог в качестве базового языка программирования. Пролог считается одним из языков искусственного интеллекта. Его название происходит от аббревиатуры PROgramming in LOGic (ПРОграммирование ЛОГики) - ПРОЛОГ. Действительно, основа языка Пролог - математическая логика. Пролог знаменует собой важный этап в эволюции языков программирования: движение от языков низкого уровня, пользуясь которыми программисты описывают, как что-либо следует делать (традиционные процедурно-ориентированные), к языкам высокого уровня, в которых указывается, что необходимо делать (декларативные языки).
Пролог - язык программирования, предназначенный для обработки символьной (нечисловой) информации. Особенно хорошо он приспособлен для решения задач, в которых фигурируют объекты и отношения между ними. Язык этот весьма прост. Его реализация содержит ограниченный набор механизмов: сопоставление образцов, древовидное представление структур данных и автоматический поиск с возвратом.
Классический Пролог относится к интерпретируемым языкам. Первый интерпретатор Пролога был написан на Фортране. Впоследствии было создано множество версий языка для разнообразнейших программно-аппаратных платформ, были даже созданы компиляторы Пролога, однако, несмотря даже на отсутствие стандартов Пролога (де факто таковым считается "марсельская" версия), его идеология, внутренние механизмы остаются неизменными.
ОПИСАНИЕ ВЗАИМООТНОШЕНИЙ МЕЖДУ ОБЪЕКТАМИ
Как уже говорилось, Пролог создан для того, чтобы описывать взаимоотношения между объектами. В этом смысле Пролог можно назвать реляционным языком. "Реляционность" Пролога является значительно более мощной и развитой по сравнению с реляционными языками, используемыми для работы с базами данных. Именно поэтому зачастую Пролог используется для создания СУБД, в которых применяются сверхсложные запросы и процедуры поиска.
Пусть у нас есть несколько объектов. Обозначим их именами a, b, c, d, e и f. Рассмотрим отношение типа "родитель" между этими объектами:
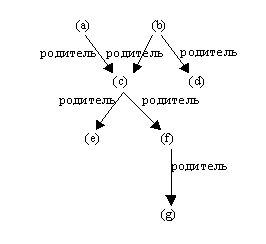
Отношения в Прологе определяются в общем случае заданием имени отношения и n-ки объектов, для которых это отношение выполняется.
На Прологе эта схема будет представлена следующей программой из 6 предложений (фактов):
родитель(a, c).
родитель(b, c).
родитель(b, d).
родитель(c, e).
родитель(c, f).
родитель(f, g).
Аргументы отношения могут быть атомами (конкретными объектами или константами) или переменными - абстрактными объектами.
Здесь объекты a, b, c, d, e, f - это атомы (константы). Обратите внимание на то, что они записываются строчными буквами. Константы на Прологе бывают символьного типа, строкового типа, а также константы - числа. В данном случае мы имеем дело именно с символьными константами. Как обычно, константа - это то, что имеет неизменное значение.
родитель - это бинарное отношение (отношение второго порядка). С тем же успехом можно было бы дополнить нашу схему, добавив отношения первого порядка. Например:
женщина (a).
мужчина (b).
мужчина (c).
и т.д.
Классический Пролог является интерактивной средой - он позволяет пользователю задавать системе вопросы и, естественно, получать на них ответы.
После ввода рассмотренной выше программы Пролог-системе можно будет задавать различные вопросы.
Синтаксис постановки вопроса на языке Пролог выглядит так:
? утверждение
Для ответа на тот или иной вопрос система ищет в базе данных имеющиеся факты и правила, подтверждающие утверждение и при нахождении таковых отвечает утвердительно, в противном случае - отрицательно. С этой точки зрения можно считать, что Пролог пытается доказать введенное в качестве вопроса утверждение.
Например:
? - родитель (a, c)
Да
? - родитель (a,e)
Нет
и т.п.
Можно задавать и вопросы вида:
?- родитель(a, X)
X = c
Да
?- родитель(X, c)
X = a
X = b
Да
?- родитель(X, Y)
X=a Y=c
X=b Y=c
X=b Y=d
X=c Y=e
X=c Y=f
X=f Y=g
Да
Таким образом, система отыщет всевозможные варианты значений переменной X. О переменных мы поговорим несколько позже, а здесь отметим лишь, что переменная - это то, что может принимать некоторые значения и обозначается именем, начинающимся с заглавной буквы.
Пролог умеет отвечать не только на такие примитивные вопросы, какие были приведены выше. Вопросы могут быть сложными, образующими логические выражения. Примером составного вопроса является вопрос вида "кто является родителем родителя?". Для того чтобы задать такой вопрос, определим понятие "родитель родителя" следующим образом.
Некто X является родителем родителя Z, если этот X - родитель некоторого Y, а этот Y является родителем для Z. Это утверждение может быть записано в виде логического выражения, представляющего коньюнкцию. В Прологе операция И обозначается ключевым словом and либо запятой:
родитель(X,Y) and родитель (Y,Z)
Найдем родителя и "деда" объекта g:
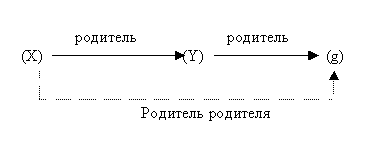
Тогда наш вопрос может выглядеть так:
?- родитель(X,Y), родитель(Y, g)
Реакция системы на этот вопрос будет заключаться в выдаче значений переменных X и Y:
X = c
Y = f
Обратите внимание на то, что наш вопрос мог быть записан и в таком виде:
?- родитель(Y, g), родитель(X,Y)
Результат будет тем же самым, однако, как это будет видно далее, эффективность поиска в этом случае будет выше.
Введем отношение "отпрыск". Можно изобразить аналогичную вышеприведенной схему отношений и ввести еще 6 предложений-фактов. Однако значительно элегантнее определить отношение "отпрыск" (отношение, противоположное отношению "родитель") следующим образом:
С точки зрения формальной логики понятие "отпрыск" можно определить так:
Для любых X и Y Y является отпрыском X, если X - родитель Y.
На Прологе это будет записано в виде следующего предложения:
отпрыск(Y,X) :- родитель(X,Y).
Подобные предложения называются правилами. Правило имеет условную часть (посылку - антецедент) и часть вывода (заключение - консеквент). Если в привычном виде правило записывается как
Если (антецедент) То (консеквент),
то в Прологе правило выглядит иначе - сначала записывается заключение, а затем посылка:
Заключение if Посылка
Посылка в Прологе называется телом правила, а заключение - головой правила.
(Голова) if (Тело)
Например, отношение родитель_родителя может быть представлено в виде правила
родитель_родителя(X,Z) :- родитель(X,Y), родитель(Y,Z).
А отношение "сестра" может быть определено так:
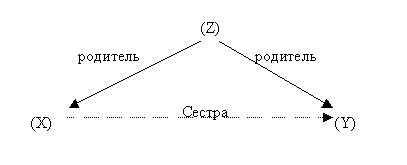
сестра(X,Y) :-
родитель(Z,X),
родитель(Z,Y),
женщина(X).
ПРОЛОГ С МАТЕМАТИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
Пролог рассматривает факты и правила в качестве множества аксиом, а вопрос пользователя - как теорему. Пролог пытается доказать эту теорему, т.е. показать, что ее можно логически вывести из аксиом.
Для примера рассмотрим известный силлогизм Аристотеля:
Все люди смертны. Сократ-человек. Следовательно, Сократ - смертен
Более формально:
(Все люди смертны = Для любого X: X - человек => X смертен)
"Х: Х - человекÞХ - смертен
Сократ - человек
Сократ смертен
На Прологе это будет выглядеть так:
смертен(X) :- человек(X).
человек(сократ).
?- смертен(сократ)
Да
ФОРМАЛИЗМ ЯЗЫКА ПРОЛОГ
Итак, подытожим вышеизложенное. С формальной точки зрения Пролог-программа состоит из предложений. Каждое предложение заканчивается точкой. Предложения Пролога состоят из головы и тела. Тело - список целей, разделенных запятыми. Запятые обозначают операцию конъюнкции.
Предложения Пролога бывают трех типов: факты, правила и вопросы.
- Факты содержат утверждения, которые всегда истинны. Факт - это предложение, у которого тело пустое.
- Правила содержат утверждения, истинность которых зависит от некоторых условий. Имеют голову и непустое тело.
- С помощью вопросов пользователь спрашивает систему о том, какие утверждения являются истинными. Вопрос - это предложение, состоящее только из тела. Вопросы к системе состоят из одного или более целевых утверждений (целей).
Переменные обозначаются идентификаторами, начинающимися с заглавной буквы.
В Прологе переменная представляет собой объект, способный принимать различные значения. Однако на этом сходство прологовской переменной с переменными в процедурных языках программирования заканчивается. Переменная в Прологе может быть либо свободной (или неконкретизированной), либо несвободной (конкретизированной).
Конкретизация переменной происходит тогда, когда по ходу вычислений вместо переменной подставляется другой объект (переменная получает конкретное значение и становится несвободной). С этого момента переменная не может принять другое значение. Переменная определяется только внутри предиката (никаких "глобальных" переменных в Прологе не существует). Строго говоря, предполагается, что на переменные действует квантор всеобщности ("для всех"). И именно в этом состоит смысл понятия переменной.
Каким же образом работает система? Когда задается вопрос, интерпретатор Пролога начинает последовательно проверять (доказывать) истинность всех составляющих его коньюнктов. Проверяя очередной коньюнкт, система начинает просмотр имеющейся базы данных и правил. С каждым из выбираемых фактов и правил Пролог сначала пытается сопоставить доказываемое утверждение.
Сопоставление термов. Все объекты данных в Прологе синтаксически представляют собой термы. Термы сопоставимы, если:
- они идентичны;
- можно конкретизировать переменные терма таким образом, чтобы они стали идентичными.
Если термы сопоставимы, то система продолжает доказывать истинность входящих в сопоставленный терм утверждений и т.д. При этом, однако, в системном стеке запоминается точка возврата - местоположение этого сопоставленного терма. Иными словами, система Пролог реализует некоторое дерево поиска, причем поиск этот осуществляется в глубину, вплоть до исчерпывания всего пути поиска. Если на очередном шаге поиска могут быть сопоставлены несколько термов, то система запоминает в стеке номера этих термов с тем, чтобы можно было в дальнейшем попытаться использовать и эти альтернативы. Именно так и осуществляется механизм поиска с возвратом.
РЕКУРСИВНЫЕ ПРАВИЛА
В Прологе нет циклов. Все итерационные процедуры осуществляются с помощью рекурсии. Кроме того, рекурсия играет, естественно, и самостоятельную роль. Например, можно определить отношение "предок" (предок в самом общем смысле) следующим образом:
предок(X,Z) :- родитель(X,Z).
предок(X,Z) :- родитель(X,Y), предок(Y,Z).
Повторение. Организовать циклические вычисления можно с помощью простого предиката repeat:
repeat.
repeat :- repeat.
Первое правило всегда истинно. Оно необходимо для создания точки возврата, когда сработает рекурсивный repeat. Следовательно, нам достаточно заставить систему перейти к альтернативному варианту, и мы тогда получим бесконечный цикл. Например, предикат echo будет запрашивать пользователя ввод строки, выводить ее на экран. И продолжаться это будет до тех пор, пока пользователь не введет строку "quit":
echo:- repeat,
write("Введите строку (quit-выход)"),
readln(S),
S="quit".
Дело в том, что в последней строке происходит сравнение введенной строки со строкой "quit". Если строки не совпадают, то система вернется к предыдущей альтернативной точке. Таковой является предикат repeat (недаром их у нас два варианта). Система пробует очередной вариант его выполнения и тем самым попадает в бесконечную рекурсию - в бесконечный цикл. А вот если строки совпадут, то тогда выполнение предиката echo будет считаться успешным.
Приведем еще один пример применения рекурсивного правила. Следующий предикат вычисляет сумму ряда:
sum(1,1).
sum(N,Sum) :-
N>0,
Next = N-1,
sum(Next,Sum2),
sum = N+Sum2.
СПИСКИ
Очень важной структурой в Прологе является список - некий аналог массива. Все списки однородные, т.е. состоят из элементов одного типа - только чисел, только строк и т.п.
Очень характерно, как определяет списки сам Пролог. В Прологе список - это структура, состоящая из головы и хвоста. Голова - это один элемент. Хвост - это список. Список может и не содержать элементов. Тогда он называется пустым списком. Правила определения списка могут выглядеть так:
Список R []
Список R Голова, Хвост
Голова R элемент
Хвост R Список
Список задается перечислением его элементов, заключенным в квадратные скобки. Разделение списка на голову и хвост происходит указанием специального разделителя - символа '|'.
Примеры списков:
[1,3,8,1,6], [a, b, ec ], ["абв", "где", "жз"]
При этом в списке [1,3,8,1,6] голова - это элемент 1, а хвост - это список [3,8,1,6]:
[ 1 | 3 , 8 , 1 , 6 ]
голова хвост
Знание того, как определяется список в Прологе, позволяет понять, как пишутся предикаты для работы с ними. Например, предикат, распечатывающий список, может выглядеть так:
print_list([]) :- !.
print_list([H|Tail]) :-
write(H),
print_list (Tail).
Другим примером может служить замечательный предикат append. Это - удивительный предикат. Он столь же прост, сколько и универсален. Если разобраться, как он работает, то можно считать, что вы как минимум наполовину знаете устройство Пролога. Выглядит он весьма просто:
append([],L,L).
append([H|A],B,[H|C]) :- append(A,B,C).
Этот предикат может конкатенировать (сцеплять) два списка, он может проверять, составляет ли конкатенация пары списков третий, он может даже разделять список на все возможные пары его составляющих. Именно это и делается в приведенной ниже программе, которая выводит на экран все возможные разбиения списка:
goal
s([1,2,3,4]).
clauses
append([],L,L).
append([H|A],B,[H|C]) :- append(A,B,C).
print_list([]) :- !.
print_list([H|Tail]) :- write(H), print_list (Tail).
s(S) :- append(L1,L2,S), print_list(L1), print_list(L2), fail.
s(_) :- !.
О том, что такое ! и fail, будет сказано ниже.
Откат после неудачи. Предикат fail всегда заканчивается неудачей. Вместо него можно было бы использовать какое-нибудь априорно ложное утверждение (например, 1=2), однако с ним программа выглядит элегантнее. Следующий предикат выводит на экран все имеющиеся имена.
show_all :-
name(X),
fail.
name("Петров").
name("Иванов").
name("Сидоров").
Если бы не fail, то выполнение предиката закончилось бы выводом одного-единственного имени. Правило выдачи на экран "эха", использующее уже знакомый repeat, но уже в бесконечном цикле, выглядит так:
echo:-
repeat,
readln(S),
write(S),
fail.
Здесь fail служит для того, чтобы реализовать откат после неудачи. Еще раз отметим, что откат происходит к repeat, т.к. в нем существует как минимум две возможности реализации repeat. Это правило порождает бесконечное число точек возврата.
Отсечение. Иногда бывает необходимо ограничить круг поиска, т.е. заставить систему "забыть" о существовании альтернативных вариантов - точек возврата. Фактически речь идет о задаче отсечения ненужных результатов. Этой цели служит предикат cut или '!' (в Прологе вообще любят все сокращать - вместо and - запятая, вместо cut - восклицательный знак, вместо or - точка с запятой ';'). Пользоваться этим предикатом нужно очень осторожно. А лучше стараться не пользоваться вовсе (во всяком случае без крайней необходимости). Этот предикат всегда истинен. Он отсекает все точки возврата, находящиеся до него (иными словами, этот предикат очищает стек точек возвратов).
Примеры использования предиката cut:
show_somebody :-
name(X), make_cut(X), !.
make_cut(X) :- X="anonymous".
echo :-
repeat,
readln(S),
write(S),
check(X), !.
check(S) :- S="stop".
check(_) :- fail.
1) Донован Дж. Системное программирование /Пер.с англ. -М.:Мир, 1975. -540с.
2) Грис Д. Конструирование компиляторов для цифровых вычислительных машин /Пер.с англ. -М.:Мир, 1975.
3) Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. В 2-х томах. Том 1. М.:Мир, 1978. -616с.
4) Керниган Б.В., Пайк Р. UNIX - универсальная среда программирования /Пер.с англ. Березко, Иващенко. Под ред. М.И.Белякова -М.:"Финансы и статистика", 1992. -304 с.
5) Р.Хантер. Проектирование и конструирование компиляторов. -М.:Финансы и статистика, 1984.