УДК 681.3.06

АНАЛИЗ БЕЗОПАСНОСТИ РЕЖИМОВ БЛОЧНОГО СИММЕТРИЧНОГО ШИФРОВАНИЯ

Сергей Головашич, Олег Лебедев

Харьковский государственный технический университет радиоэлектроники

 

Аннотация: Виконано аналіз основних режимів застосування блокових симетричних шифрів. Визначено переваги та недоліки кожного з режимів, запропоновано засоби усунення виявлених недоліків. Наведено дві схеми режимів потокового шифрування, що задовольняють запропонованим вимогам.

Summary: The symmetric block ciphers standard modes of operations analysis is carried out. The advantages and disadvantages of each mode is analysed, the improvement methods are suggested. The schemes of two new modes for stream encryption are proposed. These schemes completely satisfy suggested requirements.

Ключевые слова: Блочные симметричные шифры, режимы блочного шифрования, период гаммы шифрующей.

Введение

Неотъемлемым компонентом современных систем криптографической защиты информации являются симметричные шифры, используемые для высокоскоростного скрытия смыслового содержания больших объёмов конфиденциальной информации. Симметричные шифры принято разделять на два класса: поточные и блочные.

В открытых компьютерных системах большее распространение получили блочные шифры, в то время как классические поточные шифры обычно ориентированы на аппаратную реализацию, являются секретными и используются преимущественно в специализированных системах связи. С целью устранения недостатков, свойственных шифрам подстановки, для блочных шифров был разработан ряд режимов, предназначенных для обработки больших объёмов информации. Эти режимы фактически определяют поточные схемы шифрования, построенные на базе блочного шифра. Далее, применительно к подобным схемам, преобразование, определённое алгоритмом блочного шифрования, будем называть (базовой) функцией шифрования, а всю схему – шифратором.

Целью данного сообщения является анализ степени защищённости шифраторов, определённых стандартными режимами, от атак, используемых для нападения на блочные шифры, а также определение способов повышения безопасности этих режимов.

В общем случае основной задачей криптоаналитика, атакующего систему шифрования, является определение секретного ключа либо синтез схемы, выполняющей преобразование данных, эквивалентное расшифрованию (зашифрованию) на неизвестном ключе. Наиболее эффективные атаки криптоанализа блочных симметричных шифров строятся на основе знания криптоаналитиком как шифрованного, так и соответствующего ему открытого текста, т. е. известных пар «открытый – шифрованный текст». Эффективность многих из этих криптоатак повышается, если криптоаналитик может выбирать открытые тексты, поступающие на вход функции шифрования, т. е. атаки на основе «подобранных открытых текстов». Считается, что если функция шифрования устойчива к атакам на основе известных (подобранных) текстов, то она устойчива и к другим видам атак (атаки на основе связанных ключей учитывать не будем, т. к. они используют слабости процесса генерации ключей и для их реализации требуются «специфические» условия).

I Стандартные режимы применения блочных шифров

В 1980 г. американским стандартом FIPS Pub 81 «DES Modes of Operation» [2] и затем в 1983 г. стандартом ANSI X3.106 [3] специально для алгоритма DES было определено четыре режима применения функции шифрования DEA. В общем виде для произвольных 64–битных и n–битных блочных шифров аналогичные режимы были определены стандартами ISO 8732 [4] и ISO/IEC 10116 [5] соответственно. Стандарт ГОСТ 28147–89 [6] также определяет четыре режима криптографического преобразования данных. По назначению и структуре эти режимы аналогичны режимам, определённым в указанных выше стандартах. Исключение составляет второй режим ГОСТа (режим гаммирования). По назначению он соответствует режиму OFB, но вместо обратной связи по гамме шифрующей, использует принцип «счётчика состояний». Подобная схема ранее была предложена Диффи и Хеллманом [7]. Рассмотрим все режимы, определённые указанными стандартами:

·   Electronic Codebook (ECB) ¾ режим электронной кодовой книги (ГОСТ: режим простой замены);

·   Output Feedback (OFB) ¾ режим обратной связи по выходу;

·   Cipher Feedback (CFB) ¾ режим обратной связи по шифртексту (ГОСТ: режим гаммирования с обратной связью);

·   Cipher Block Chaining (CBC) ¾ режим связки шифроблоков (ГОСТ: режим выработки имитовставки);

·   «Counter» mode ¾ режим «счётчика» (ГОСТ: режим гаммирования).

Большинство перечисленных режимов определяют поточные шифраторы. Они делятся на два класса: синхронные и самосинхронизирующиеся. В синхронных шифрах гамма шифрующая формируется независимо от обрабатываемого текста и определяется только ключом шифрования и внутренним состоянием шифратора. В самосинхронизирующихся шифрах гамма формируется как функция от ключа шифрования и некоторого фиксированного количества ранее сформированных символов криптограммы [1]. Для рассматриваемых схем отдельному символу будет соответствовать блок текста, обрабатываемый за одну итерацию шифрования.

II Режим ECB

В режиме электронной кодовой книги (ECB) базовая функция шифрования применяется без дополнительных преобразований, т. е. отдельные блоки открытого текста независимо зашифровываются в блоки криптограммы.

Для этого режима свойственны все недостатки шифров подстановки: одинаковые блоки открытого текста отображаются на одинаковые блоки криптограммы; перестановка блоков криптограммы приводит к соответствующей перестановке блоков открытого текста и наоборот; модификация любого блока открытого текста после зашифрования сказывается только на соответствующем блоке криптограммы и наоборот. Независимость обработки отдельных блоков часто приводит к невозможности скрытия структуры защищаемой информации. При определённых обстоятельствах это позволяет криптоаналитику получить интересующую информацию о зашифрованном сообщении только на основе криптограммы, без поиска ключа шифрования. Поэтому применение данного режима для обработки сообщений, превышающих один блок, не рекомендуется.

В этом режиме возможен криптоанализ базовой функции шифрования на основе «известных» и «отобранных» открытых текстов, т. к. значения входа I_i и выхода O_i функции шифрования соответствуют блокам открытого текста и криптограммы.

III Режим OFB

Шифратор, определяемый режимом обратной связи по выходу (OFB), фактически соответствует поточному синхронному шифру. При этом размерность пространства состояний определяется длиной блока (входа) функции шифрования, а размерность выходного алфавита определяется длиной блока гаммы. В этом режиме блоки гаммы шифрующей Г_i и блоки обратной связи B_i формируются на основе выхода базовой функции шифрования. В общем случае блоки Г_i и B_i могут иметь некоторые длины r и t, меньшие, чем длина блока n базовой функции шифрования и формироваться как произвольные подмножества выходных битов функции E_K. Стандарт FIPS Pub 81 [2] предполагает возможность реализации OFB режима с идентичными блоками гаммы и обратной связи произвольной длины, т. е. r = t, 1 Ј r Ј n, B_i = Г_i.

Рассмотрим принципы выбора параметров r и t. Учитывая, что функция шифрования E_K определяет перестановку на множестве n–битных блоков, и предполагая, что для случайного ключа K перестановка E_K выбирается действительно случайно из пространства всех возможных (2ⁿ)! перестановок, можно показать, что для случайно выбранных ключа и начального состояния ожидаемая длина цикла, до повторения состояния, будет равна приблизительно 2^n–1. С другой стороны, если r < n, то выходная последовательность формируется в соответствии с некоторой итеративной функцией, не являющейся перестановкой, и при допущении, что она ведёт себя как случайная функция, ожидаемая длина цикла будет порядка 2^n/2 [1]. В связи с этим при реализации OFB режима рекомендуется использовать полную обратную связь (n бит). Такое требование предъявляется стандартом ISO/IEC 10116 [5]. Однако следует отметить, что для большинства блочных шифров задача доказательства (определения) минимально-возможного цикла, а следовательно, и минимального периода гаммы в этом режиме на полном пространстве допустимых ключей и начальных состояний является трудно разрешимой. В связи с этим возможна ситуация когда для некоторых значений ключа шифрования и начальных состояний длины циклов будут очень короткими, что может привести к повторению последовательности гаммы шифрующей при обработке больших потоков информации. С другой стороны, использование блоков гаммы длиной меньше n бит ограничивает возможности атакующего изучать свойства функции шифрования на основе известных пар «открытый–шифрованный» текст и, следовательно, усложняет задачу поиска ключа шифрования.

Данный режим обеспечивает большую надёжность, чем ECB и предлагается в качестве одного из основных режимов шифрования больших потоков данных. Но этот режим также не «скрывает» функцию шифрования от атак на основе известных пар текстов. Так если криптоаналитику известен открытый текст для некоторой цепочки последовательных блоков криптограммы, тогда первый блок цепочки пропускается, т. к. для этого блока состояние шифратора полностью не определено, а начиная со второго блока цепочки входное значение может быть вычислено как XOR (сложение по модулю 2) предыдущего блока криптограммы C_i–1 с соответствующим ему блоком открытого текста M_i–1. При этом следует учитывать, что значение синхромаркера, используемое для инициализации шифратора на первом цикле, является открытой величиной и подаётся на вход функции шифрования в исходном виде. Поэтому, если известная криптоаналитику цепочка начинается с первого блока, то для построения атаки могут использоваться все известные блоки, начиная с первого. Для случая «полной» (n–битной) обратной связи имеем:

I_i = C_i–1 Е M_i–1, O_i = C_i Е M_i.

IV Режим CFB

Шифратор, определяемый режимом обратной связи по шифртексту (CFB), фактически соответствует поточному самосинхронизирующемуся шифру. При этом, как и для OFB режима, размерность пространства состояний шифратора определяется длиной блока (входа) функции шифрования, а размерность выходного алфавита определяется длиной блока гаммы. Символы гаммы шифрующей формируются как некоторое подмножество выходных битов функции шифрования, т. е. длина блока гаммы r может быть меньше длины блока n базовой функции шифрования. В качестве обратной связи используется блок криптограммы, поэтому её разрядность также равна r. Стандарт ГОСТ 28147‑89 (режим гаммирования с обратной связью) предусматривает использование только полной n-битной обратной связи.

Режим CFB, как и OFB, позволяет атаковать базовую функцию шифрования на основе известного открытого текста: входное значение функции шифрования соответствует ранее полученному шифртексту либо синхромаркеру для первого блока криптограммы, а выход функции шифрования может быть получен как XOR блоков криптограммы и соответствующего известного открытого текста. Для случая «полной» (n–битной) обратной связи имеем:

I_i = C_i–1, O_i = C_i Е M_i.

Кроме того, если полученная криптограмма содержит две одинаковые последовательности блоков длиной йn / rщ, значит открытый блок, следующий за каждой из этих последовательностей, будет зашифрован идентичным значением гаммы, однако при ограниченной длине текста L (такой, что L²<<2ⁿ) вероятность такого совпадения, в соответствии с парадоксом «дня рождения», является довольно низкой.

V Режим CBC

Режим связки шифроблоков (CBC) по своим возможностям подобен режиму с обратной связью по шифртексту (CFB). Однако в отличие от CFB‑режима, в режиме CBC операция блочного шифрования выполняется после «связывания» текущего блока с предшествующим, а при расшифровании используется обратная схема. Вследствие использования для обратного преобразования базовой функции блочного расшифрования, режим может манипулировать только блоками текста полной длины n.

Основное достоинство данного режима перед CFB заключается в том, что последний блок криптограммы является ключезависимой нелинейной функцией от всех блоков криптограммы (в CFB‑режиме последняя пара блоков открытого и шифрованного текстов связана функцией XOR). Это свойство позволяет использовать последний блок криптограммы (или его часть) в качестве кода аутентификации сообщения, т. е. получать код аутентификации L–блочного текста за L шагов. В соответствии с американскими и международными стандартами [2–5] этот режим может применяться как для шифрования, так и для аутентификации сообщений, в то время как аналогичный режим стандарта ГОСТ 28147–89 (режим выработки имитовставки) применяет функцию шифрования с сокращённым вдвое числом циклов и предписывает использование этого режима только для целей аутентификации, т. е. промежуточные блоки криптограммы не сохраняются.

Режим CBC, как и предыдущие режимы, позволяет атаковать непосредственно базовую функцию шифрования на основе пар известного (подобранного) открытого текста: входное значение функции шифрования может быть вычислено как XOR предыдущего блока шифртекста и текущего блока открытого текста, а выход функции шифрования соответствует текущему блоку криптограммы:

I_i = M_i Е C_i–1, O_i = C_i.

Кроме того, если два соседних блока шифртекста появляются в криптограмме более одного раза, то значит второй блок в этой паре соответствует одинаковым блокам открытого текста, хотя, при ограниченной длине текста (L²<<2²ⁿ), вероятность такого совпадения пренебрежительно мала.

VI Режим «счётчика»

Режим гаммирования в соответствии с ГОСТ 28147–89, как и режим OFB (в соответствии с FIPS), определяет шифратор, соответствующий поточному синхронному шифру, однако использует принцип «счётчика». В отличие от OFB, данный режим ГОСТа предполагает использование блоков гаммы полной длины n.

Данный режим ГОСТа использует значение зашифрованного базовой функцией синхромаркера (открытый параметр) S₀ = E_K(SYN) в качестве начального состояния n – разрядного линейного конгруэнтного генератора с известным большим периодом (близким к 2ⁿ). Блоки гаммы получаются путём шифрования базовой функцией «задающей» последовательности, формируемой указанным генератором. Использование подобной схемы позволяет обеспечить доказуемый фиксированный период выходной гаммы при любом ключе шифрования и любом начальном состоянии (синхромаркере). Кроме того, при такой схеме невозможен криптоанализ функции шифрования на основе известных пар текстов, т. к. вход функции шифрования не может быть получен из открытого и зашифрованного текста путём применения тривиальных (не зависящих от ключа) преобразований.

Данная схема также обладает рядом недостатков. Так использование в качестве генератора «счётчика» с известным коэффициентом приращения приводит к тому, что атакующему известна дифференциальная разность любой пары элементов «задающей» последовательности. При «слабой» функции шифрования это свойство может быть использовано для построения атаки дифференциального криптоанализа. Кроме того, формируемая последовательность блоков гаммы шифрующей является периодичной, т. е. появление идентичных значений гаммы невозможно для соседних ±T блоков, где T – период гаммы, обеспечиваемый генератором. Это даёт криптоаналитику дополнительную информацию, особенно при наличии большого объёма известного открытого текста.

Рассматриваемый режим, в отличии от OFB, обладает свойством «произвольного доступа», т. е. возможностью выполнять зашифрование/расшифрование фрагментов потока с произвольным смещением. При этом, в отличие от CFB‑режима, не требуется знания дополнительных блоков криптограммы. Потребность в указанном свойстве возникает при реализации функций «прозрачного» шифрования в устройствах хранения информации с произвольным доступом. Данное свойство обусловлено наличием вычислительно простого не итеративного соотношения:

S_i = G ^*(S₀, i ).

Наиболее простым генератором, удовлетворяющим указанному свойству, является «счётчик» – накапливающий сумматор с фиксированной величиной приращения.

VII «Счётчик» с фиксированным периодом

Рассмотрим способы построения генераторов «задающей» последовательности типа «счётчик» и их свойства.

Наиболее простым (классическим) «счётчиком» является схема, удовлетворяющая соотношению G₁(X) = (X + 1) mod M. Очевидным является факт, что период рекуррентной последовательности вида X_i+1 = G₁(X_i ) будет равен M при любом начальном значении X_0. Однако существенным недостатком данной схемы является то, что при L << M элементы последовательности (X_i, ... , X_i+L) будут отличаться друг от друга только в младших разрядах. Поэтому использование подобной «задающей» последовательности приводит к ограниченной «активизации» входов функции шифрования, что может быть использовано для повышения эффективности криптоанализа базовой функции.

В связи с этим более предпочтительной является следующая обобщённая схема:

                                                          G_C (X) = (X + C) mod M.                                                        (1)

Утверждение 1. Если конгруэнтный генератор вида:

                                                                   X_i+1 = G_C (X_i)                                                                  (2)

удовлетворяет требованию (C, M) = 1, то формируемая этим генератором последовательность {X_i} для любой начальной точки X₀ будет пробегать все значения в диапазоне 0, ... , M–1 и соответственно иметь максимальный период повторения, равный M.

Указанное свойство следует из теории вычетов [8], если учесть, что любой элемент последовательности (2) может быть записан в следующем виде:

                                                          X_i = (X₀ + C ґ i) mod M.                                                         (3)

Использованный в соотношении (1) коэффициент C определяет величину приращения (шаг) генератора вида (2). Его выбор определяет свойства формируемой последовательности, поэтому для обеспечения максимального периода необходимо проверять условие (C, M) = 1, а для улучшения статистических свойств формируемых последовательностей – накладывать ограничение на длины 1- и 0-вых битовых серий.

Основным недостатком генераторов вида (3), как было отмечено выше, является фиксированная дифференциальная разность для любой пары элементов последовательности:

DX_ij = C ´ (j – i) mod M.

При этом указанная зависимость между элементами «задающей» последовательности, даже в случае секретного (зависящего от ключа и синхромаркера) коэффициента C, может быть использована для криптоанализа функции шифрования.

Отметим, что режим гаммирования ГОСТа использует генератор, построенный на двух «параллельных» 32-битных счётчиках и обеспечивает период T = 2⁶⁴ – 2³². Этому генератору присущи все выше рассмотренные свойства.

VIII Пути повышения безопасности стандартных режимов

Как было показано выше, все рассмотренные режимы обладают определёнными недостатками. Определим принципы построения поточных схем шифрования на базе блочных криптоалгоритмов, устраняющие обнаруженные слабости:

1.   Период гаммы, формируемой шифратором, должен удовлетворять некоторой нижней границе T_min при любом ключе шифрования и векторе инициализации.

2.   Функция смены состояний (формирования «задающей» последовательности) должна быть нелинейной и ключезависимой.

3.   Шифратор должен скрывать своё текущее состояние, а его выход (блок гаммы Г_i) должен оставлять неопределённость относительно текущего состояния шифратора S_i, т. е. пространство состояний должно превышать пространство выходов.

Применение приведенных выше принципов построения поточных режимов шифрования позволяет минимизировать, по сравнению со стандартными режимами, количество дополнительной информации, которую может извлечь криптоаналитик из известных пар текстов.

Для реализации первого принципа при построении шифратора в качестве основы может использоваться схема на базе «счётчика», гарантирующая необходимый период.

Для реализации второго принципа критичный параметр генератора (величина приращения «счётчика») может быть сделан динамически изменяемой величиной и вычисляться как функция от ключа шифрования и текущего состояния, т. е. указанный параметр может формироваться по принципу OFB‑ (CFB‑) режима. Однако такое решение вступает в конфликт с реализацией первого принципа. Для решения этого противоречия можно предложить использовать схему на базе «счётчика» с «плавающим» периодом, рассмотренную далее.

Для реализации третьего принципа необходимо, чтобы каждый блок гаммы формировался путём криптографического «сжатия» текущего внутреннего состояния шифратора. Наиболее простым решением этой задачи при идентичной разрядности генератора и базовой функции шифрования является формирование блоков гаммы как некоторого подмножества выходных битов функции шифрования. Тогда, если используется m–разрядный генератор и число его состояний M » 2^m, а выход шифратора составляет n разрядов (m > n), то при условии равновероятного распределения выходных значений шифратора по состояниям генератора вероятность «угадывания» состояния шифратора по известному блоку гаммы (при фиксированном ключе) составит 2ⁿ / M » 2 ^n – m.

В случае выполнения последнего требования становится возможным повторение отдельных блоков гаммы в пределах периода, что позволяет сократить информацию о состоянии криптосистемы и открытом тексте, которые атакующий может извлечь из перехваченной криптограммы.

Для дальнейшего изложения воспользуемся следующими обозначениями для определения операций над n ‑ разрядными целыми числами x и y:

·     x [+]_n y = (x + y) mod 2ⁿ;

·     x {+}_n y = ( (x + y) + (x + y) / 2ⁿ ) mod 2ⁿ;

·     {++} _n x = x {+}_n 1.

Первая операция соответствует обычному n–разрядному суммированию. Вторая и третья операции, соответственно, определяют функции сложения и инкрементирования по модулю 2ⁿ‑1, при этом в области значений результата выполняется замена 0 ® 2ⁿ – 1, т. е. «запрещённым» является значение 0. Преимуществом второй операции перед обычным сложением является влияние каждого разряда аргумента на все разряды результата. Аппаратно эти функции реализуются на основе обычного сумматора путём дополнительного прибавления бита внешнего переноса (переполнения) к младшему разряду результата.

IX «Счётчик» с «плавающим» периодом

Рассмотрим принципы построения и свойства криптографически стойких генераторов типа «счётчик» с динамически изменяемым коэффициентом приращения.

Определение 1. Под генератором псевдослучайных чисел с «плавающим» периодом (либо «плавающим» ГПСЧ) будем понимать ГПСЧ, формирующий последовательность чисел с переменным периодом T, зависящим от начального состояния S₀ и управляющего параметра K генератора, фактическое значение которого всегда находится в диапазоне предельных значений: T_min < T = l(S₀, K) < T_max.

Определение 2. Счетчиком с «плавающим» периодом будем называть «плавающий» ГПСЧ, удовлетворяющий следующим рекуррентным соотношениям:

S_i+1 = S_i [+]_m (C ґ N_i ), N_i = {++}_n H_K (S_i ),

где   m – разрядность «счётчика»;

n – разрядность нелинейной обратной связи;

С – «коэффициент подъёма» (нечётная константа, т. к. (C, 2^m) = 1 );

S_i – состояние генератора на шаге i (разрядность m бит);

N_i – «шаг подъёма» на шаге i (разрядность n бит);

K – управляющий параметр генератора (ключ шифрования);

H_K – криптографическая функция нелинейного «сжатия» S_i ® N_i (m > n), параметризованная ключом K.

«Шаг подъёма» N_i в последнем соотношении отражает количество «шагов» базового «счётчика» с фиксированным периодом отделяющих состояния S_i и S_i+1. При этом необходимым требованием является условие N_i і 1, для его обеспечения используется операция {++}_n. Величину C ґ N_i назовём динамически изменяемым приращением счётчика.

Отметим, что «счётчик» с фиксированным периодом может рассматриваться как частный случай «счётчика» с «плавающим» периодом, когда "i выполняется N_i = 1. Кроме того, вместо операции [+]_m возможно применение операции {+}_m, тогда (C, 2^m – 1) = 1.

Утверждение 2. Период m–разрядного «плавающего» счётчика с n–разрядным «шагом подъема» при любых начальном состоянии S₀ и управляющем ключе K будет находиться в интервале: 2^m–n < T Ј 2^m.

Указанное свойство является следствием двух предельных случаев: учитывая, что нелинейная функция H_K является «сжимающей» (m > n), можно предположить, что при некоторых значениях K и S₀ для всех элементов последовательности S_i выполняется одно из следующих условий:

1)         если N = H_K (S_i ) = 1, "i, то T = T_max = M / N = 2^m;

2)         если N = H_K (S_i ) = 2ⁿ – 1, "i, то T = T_min = M / N = 2^m / (2ⁿ – 1) » 2^m‑n.

Величина неопределенности криптоаналитика относительно «расстояния» (дифференциальной разности) между любыми двумя соседними состояниями S_i и S_i+1 определяется ключезависимой нелинейной обратной связью – «шагом подъёма» N_i. Увеличение разрядности этой обратной связи n будет повышать неопределённость указанного «расстояния», но в то же время снижать нижнюю границу возможного периода генератора T_min. Поэтому компромиссным решением является выбор разрядности обратной связи n = m / 2.

Следует отметить, что для «счётчиков» большой разрядности (m > 2r, где r – разрядность регистров базового процессора) операция C ґ X в общем случае является сравнительно трудоёмкой. Однако учитывая, что величина приращения состояния DS_i, i+1 зависит от трудно предсказуемого «шага подъёма» N_i, использование открытого значения C в шифраторах на базе «плавающего счётчика» не приводит к существенному снижению общей стойкости. Поэтому в таких схемах значение C может быть постоянным и выбираться с учётом оптимизации производительности (например, умножение на константу C = 2^m‑r + ... + 2^r + 1 может быть реализовано только командами сложения определённых регистров, содержащих X).

X «Усиленные» режимы поточного шифрования

В качестве примера рассмотрим несколько схем поточных синхронных шифров на базе «плавающего счётчика» и функции блочного шифрования с длиной блока n, равной разрядности «счётчика». В предлагаемых схемах выход функции шифрования разделён на две равные составляющие (по n/2 бит):

1)   блок гаммы текста Г^T_i используется для зашифрования/расшифрования i–го блока текста;

2)   блок гаммы обратной связи Г^FB_i формирует обратную связь, определяющую величину «шага подъёма» N_i.

При условии применения стойкой функции блочного шифрования каждая из указанных половинок может рассматриваться как результат однонаправленного криптографического «сжатия» текущего состояния шифратора S_i двумя различными функциями. Так как размер выходного слова шифратора (гаммы текста) и соответственно единицы обработки текста равен n/2, то под блоком далее будем понимать вектор длиной n/2 бит.

На рис. 1 приведена структурная схема усиленного режима поточного шифрования «с последовательным доступом». Период гаммы шифрующей для этой схемы будет «плавающим» в диапазоне 2^n/2 < T Ј 2ⁿ, а его фактическое значение будет зависеть от ключа шифрования K и вектора инициализации (синхропосылки SYN).

Процедуры зашифрования и расшифрования для этого режима могут быть описаны следующими соотношениями:

S₀ = E_K (SYN), N₀ = 1, i = 1 ... L,

S_i = G(S_i–1 , N_i–1 ) = S_i–1 [+]_m (C ґ N_i–1 ), N_i = {++}_n/2 Г^FB_i,

{Г ^FB_i , Г ^T_i} = E_K (S_i ),

Г ^T_i = E_K (S_i ) (mod 2^n/2), Г ^FB_i = E_K (S_i ) / 2^n/2,

C_i = M_i Е Г ^T_i, M_i = C_i Е Г ^T_i,

где Г ^FB_i – значение гаммы обратной связи для i-го шага (блока), Г ^T_i – значение гаммы текста для i-го шага (блока).

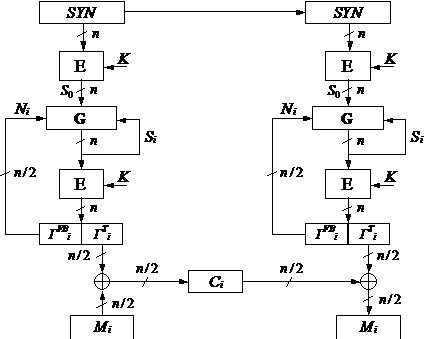
Рисунок 1 – Схема усиленного режима поточного шифрования

Данная схема объединяет достоинства OFB‑режима (нелинейная ключезависимая обратная связь) и режима «счётчика» (гарантированный период). Однако в отличие от OFB‑режима, входные значения функции шифрования недоступны криптоаналитику, а, в отличие от режима гаммирования ГОСТа, разность между элементами «задающей» последовательности неизвестна и изменяется на каждом шаге. Также возможно появление идентичных блоков гаммы текста в пределах одного периода.

Рассмотренная выше схема может быть адаптирована для выполнения одновременно с процессом шифрования функций аутентификации исходного сообщения, т. е. вычисления имитовставки. Такая модификация исходной схемы не приводит к снижению безопасности криптосистемы. Соответствующая структурная схема режима поточного шифрования с аутентификацией приведена на рис. 2.

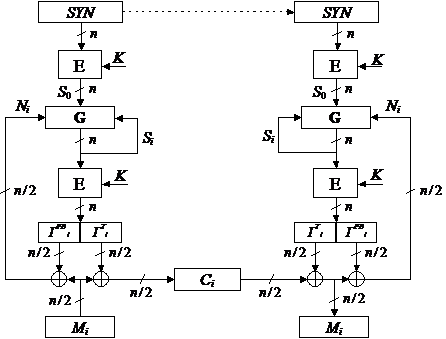
Рисунок 2 – Схема усиленного режима поточного шифрования с аутентификацией

Соотношения, описывающие процесс прямого и обратного преобразования для этой схемы, аналогичны соотношениям базовой схемы. Исключение составляет выражение для «шага подъёма»:

N_i = {++}_n/2 (M_i Е Г ^FB_i).

В соответствии с последним соотношением «шаг подъёма» N_i является функцией от блока открытого текста M_i и криптографически «сжатого» образа текущего состояния Г ^FB_i, т. е. можно сказать, что обратная связь, аналогично CFB‑режиму, представляет собой блок «внутренней» криптограммы, значение которой не выходит за пределы шифратора. Благодаря использованию не пересекающихся векторов в качестве гаммы обратной связи и гаммы текста наличие известной пары «открытый–шифрованный» текст не позволяет определить значение обратной связи N_i. На основе указанной пары криптоаналитик может определить только поток гаммы текста (Г ^T₁, ... , Г ^T_L , Г ^T_L+1), каждый из блоков которой при фиксированном (неизвестном) ключе K и «хорошей» функции E_K с вероятностью 2^–n/2 мог быть получен в одном из 2^n/2 состояний (при L << T_min). Кроме того, в отличие от CFB‑режима, данная схема свободна от недостатка «выявления коллизий», т. е. обнаружение в потоке криптограммы совпадающих блоков не увеличивает информацию криптоаналитика о неизвестных блоках гаммы шифрующей и открытого текста.

Предлагаемая схема объединяет достоинства CFB‑режима и схем на базе «счетчиков». В этой схеме состояние шифратора перед обработкой очередного блока текста зависит от предыдущего состояния и обработанного на прошлом шаге блока сообщения. Иначе говоря, текущее состояние шифратора зависит от исходного вектора инициализации (синхропосылки), всех обработанных блоков сообщения и ключа шифрования. При этом влияние последнего блока текста на вектор очередного состояния носит линейный предсказуемый характер. Поэтому для получения кода аутентификации сообщения после обработки всех блоков сообщения необходимо выполнить ещё один дополнительный шаг «шифрования», после чего выход функции шифрования {Г^FB_L+1, Г^T_L+1} либо его часть может использоваться в качестве криптографической контрольной суммы – имитовставки.

Для последней схемы понятие периода отсутствует, так как очередное состояние шифратора определяется не только текущим состоянием, но и значением обрабатываемого блока данных. Однако использование n‑разрядного «плавающего счётчика» с n/2‑разрядным «шагом подъема» позволяет гарантировать, что шифратор может оказаться в состоянии, равном данному, не ранее, чем через 2^n/2 шагов (блоков текста).

Безопасность обеих «усиленных» схем поточного шифрования зависит от длины блока базовой функции шифрования, определяющего минимальный период шифратора. Для современных коммерческих приложений, предъявляющих повышенные требования к уровню безопасности, можно рекомендовать использование в качестве базового алгоритма блочные шифры с длиной блока не менее 256 бит, т. е. длины блоков гаммы текста и обратной связи составляют по 128 бит, а минимальный период – T_min = 2¹²⁸.

Выводы

Проведенный анализ стандартных режимов применения блочных шифров показал существование у криптоаналитика потенциальной возможности атаковать непосредственно базовую функцию блочного шифрования на основе известных пар «открытый–шифрованный текст» в любом из режимов, предусмотренных международным стандартом ISO/IEC 10116 и соответствующих режимах ГОСТ 28147‑89. Кроме того, в режиме ECB возможно построение атак на основе «подобранных» открытых текстов. Режим CBC также позволяет выполнять атаки такого типа, но для этого атакующему необходима возможность динамически формировать очередной блок открытого текста по значению последнего блока криптограммы. Реализация подобной атаки для CFB‑режима теоретически возможна, но требует от криптоаналитика наличия «специального» доступа к аппаратуре шифрования, позволяющего определить значение блока гаммы до момента формирования обратной связи. Другим недостатком режимов ECB, CFB и CBC является возможность обнаружения коллизий (повторение блоков открытого текста либо гаммы) по шифрованному тексту, хотя вероятность возникновения таких коллизий в режимах CFB и CBC при длине блока 128 и более бит является сравнительно низкой. Основным недостатком режима OFB, кроме отмеченных выше, является зависимость периода гаммы шифрующей от свойств базовой функции шифрования и сложность доказательства его нижней границы. Режим «счётчика» (режим гаммирования ГОСТа) также обладает рядом недостатков: использование на входе функции шифрования «задающей» последовательности с известными дифференциальными свойствами, а также однозначное соответствие блока гаммы текущему состоянию шифратора и, как следствие, невозможность появления идентичных блоков гаммы в пределах одного периода.

Для устранения обнаруженных слабостей стандартных режимов при построении перспективных схем поточного шифрования на базе блочных симметричных криптоалгоритмов можно рекомендовать придерживаться приведенных выше принципов. Учитывая требование второго принципа (использовать криптографически   стойкую     функцию     смены    состояний),     можно    заключить,   что  в  приложениях, предъявляющих повышенные требования к безопасности конфиденциальной информации, не следует использовать шифраторы «с произвольным доступом», т. к. принцип их построения противоречит этому требованию.

Обе приведенные в статье схемы шифраторов «с последовательным доступом» удовлетворяют указанным выше требованиям и могут рекомендоваться в качестве альтернативных режимов применения блочных шифров. Стойкость приведенных схем может быть повышена путём сокращения длины блока гаммы текста, однако «ценой» за такое «усиление» будет снижение общей производительности шифратора, что для ряда приложений может быть вполне приемлемо.

 

Литература: 1. A. Menezes, P. van Oorschot, and S. Vanstone, Handbook of Applied Cryptography, CRC Press, 1996. 2. FIPS 81, «DES modes of operation», Federal Information Processing Standards Publication 81, U. S. Department of Commerce / National Bureau of Standards, National Technical Information Service, Springfield, Virginia, 1980. 3. ANSI X3.106, «American National Standard for Information Systems – Data Encryption Algorithm – Modes of Operation», American National Standards Institute, 1983. 4. ISO 8732, «Banking – Key management (wholesale)», International Organization for Standardization, Geneva, Switzerland, 1988 (first edition). 5. ISO/IEC 10116, «Information processing – Modes of operation for an n–bit block cipher algorithm», International Organization for Standardization, Geneva, Switzerland, 1991 (first edition). 6. ГОСТ 28147‑89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования. М.: Госстандарт СССР. 7. W. Diffie and M. E. Hellman, «Privacy and authentication: An introduction to cryptography», Proceedings of the IEEE, 67 (1979), pp. 397–427. 8. Ш. Х. Михелович. Теория чисел. М.: «Высшая школа», 1962. 259 с.