УДК 681.3.06: 519.248.681
и.В. Лисицкая, канд. техн. наук, В.И. Руженцев
Цепи ФЕстеля и дифференциальный Криптоанализ
На сегодняшний день не вызывает
сомнения тот факт, что будущее информационных технологий неразрывно связано с
совершенствованием методов и способов обеспечения конфиденциальности
информации. Неоспорима также огромная роль симметричных блочных шифров в
решении этого вопроса, так как данный класс шифров обладает наибольшей
скоростью выполнения операций шифрования-дешифрования, чем и обусловлено
широкое применение этих шифров. Однако, хороший симметричный блочный шифр
должен отвечать ряду требований, среди которых одними из основных являются
условия обеспечения стойкости шифра к различным видам криптоаналитических атак.
В числе наиболее мощных криптоаналитических атак – дифференциальный
криптоанализ (ДК). В этой связи актуальной представляется задача исследования
вопроса о том, как модель шифра влияет на его стойкость к атакам
дифференциального криптоанализа.
Сегодня существует несколько моделей шифров. В разных
источниках приводятся различные классификации, но чаще всего выделяют шифры,
построенные с использованием цепей Фестеля (DES, DEAL, E2,
LOKI97, RC6, Twofish, MARS), и шифры, которые построены на основе чередования
процедур перестановок и подстановок (SPN – substitution-permutation network) (Square,
Rijndael, SAFER+, Serpent, CRYPTON).
Цепь
Фестеля или конструкция Фестеля предполагает разбиение исходного
информационного блока, в общем случае, на n подблоков. На каждом цикле
одна из частей подвергается преобразованию при помощи криптографического
преобразования F. Результат операции суммируется по модулю 2 (операция XOR) с
другой частью, и подблоки меняются местами. Классической схемой Фестеля
считается вариант для n = 2, который представлен на рис. 1,а. Существуют
также расширенные цепи Фестеля для n > 2 (см. пример для n = 4
на рис. 1,б).
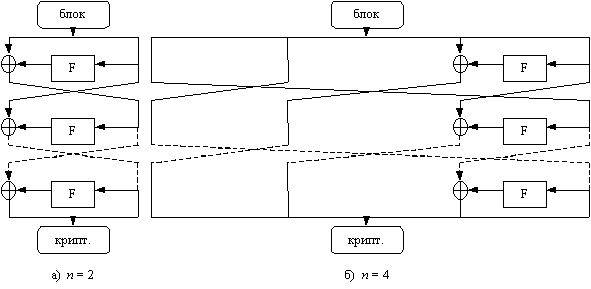
Рис. 1
Преимущество конструкции Фестеля заключается, в первую очередь, в том,
что прямое и обратное криптографические преобразования для блочного шифра имеют
идентичную структуру, вследствие чего аппаратная реализация будет более
компактной в сравнении с шифрами, для которых прямое и обратное преобразования
отличаются. Кроме этого, конструкция Фестеля по сравнению с SPN-конструкцией
позволяет использовать в шифрующей функции более широкий набор преобразований,
так как к ним не предъявляется требование обратимости. Наиболее известным
примером фестелеобразного шифра, построенного на необратимой цикловой функции,
является DES [1].
SPN-конструкция предполагает последовательное применение
шифрующей функции, которая работает не с частями информационного блока, а сразу
со всем блоком. Все преобразования в SPN-шифрах должны
быть обратимыми, так как расшифрование производится путем выполнения обратных
преобразований в обратном порядке.
При
сравнении двух классов шифров будем привязываться к скорости выполнения
криптографических преобразований. Поскольку при полном распараллеливании
скорости выполнения одного цикла преобразований для SPN-структуры
и структуры Фестеля примерно равны (хотя SPN-структура
в этом случае требует большего распараллеливания), то будем сравнивать представителей
этих классов с равным числом циклов.
В
соответствии с классической работой Шеннона шифрующие функции состоят из
операций перемешивания (нелинейные S-подстановки),
рассеивания (битовые Р-перестановки), введения секретности (сложение с ключом).
На рис. 2 представлены шифрующие функции для шифров с 16-битными
информационными блоками, построенных с использованием классической цепи Фестеля
(рис. 2,а – биективная шифрующая функция, рис. 2,б - с использованием сжимающе-расширяющих преобразований)
и по схеме SPN (рис. 2,в).
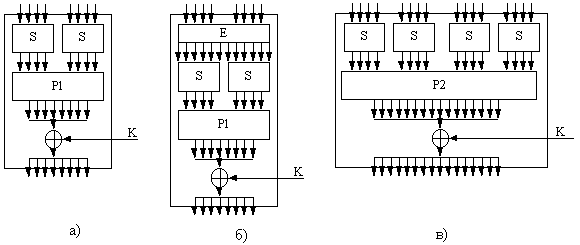
Рис. 2
Следует отметить, что сжимающие подстановки позволяют достигнуть более
хороших дифференциальных показателей, чем, видимо, и обусловлено их применение.
Но, вместе с тем, они менее удобны в реализации, так как требуют больше памяти
для хранения.
Расширяющая
перестановка Е на рис. 2,б преобразует 8-битное значение в 12-битное путем
дублирования определенных битов подобно аналогичной перестановке алгоритма DES [1].
Битовые
перестановки обычно строятся, исходя из принципа, чтобы входное значение
каждого S-блока зависело от максимального числа S-блоков предыдущего цикла. В соответствии с этим принципом
перестановки Р1 и Р2 выходные биты каждого S-блока
поровну распределяют между всеми S-блоками следующего
цикла.
Теперь
напомним основные принципы проведения дифференциального криптоанализа.
Дифференциальная атака на SPN-шифр проводится
аналогично дифференциальному криптоанализу фестелеобразного шифра,
предложенного и детально описанного в работах [2, 3]. Целью дифференциального
криптоанализа является определение битов подключа, используемого в последнем
цикле. При выполнении дифференциального криптоанализа DES-подобного
шифра для определения битов подключа используются известные входные в последний
цикл значения (непосредственные значения правых половин шифртекстов) вместе с
вероятностным значением разности на выходе шифрующей функции последнего цикла.
Аналогично, дифференциальный анализ SPN-шифра
использует известные выходные значения (шифртексты) и вероятностное значение
входной разности. Таким образом, основой построения и реализации
дифференциальных атак является использование дифференциальных характеристик
(ДХ), описывающих прохождение через циклы шифрования специфических пар открытых
текстов. Если удается найти ДХ с высокой вероятностью, то можно ставить и
решать задачи криптоанализа со сложностью меньшей, чем прямой перебор ключей
(атака грубой силой).
Очевидно,
что для 16-битового SPN-шифра, шифрующая функция которого представлена на рис.
2, в, граничное (максимальное) значение вероятности r-цикловой ДХ, при условии,
что можно оставаться в рамках одного активного S-блока на каждом цикле,
составляет
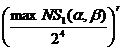 ,
a, b Î
{0,1}4 (a ¹ 0), (1)
,
a, b Î
{0,1}4 (a ¹ 0), (1)
где max NS(a, b)
обозначает максимальное значение в таблице дифференциальной разности.
Существенным
моментом при построении атак ДК на фестелеобразный шифр является возможность
использования при построении ДХ тривиальных циклов. Тривиальные циклы хороши
тем, что они не уменьшают общую вероятность ДХ (нулевая разность на входе цикла
переходит в нулевую разность на выходе с вероятностью 1). Если обозначить
разность на входе отдельно взятого цикла через D,
то речь идет о характеристиках, которые используют в отдельных циклах переход
входной разности D = 0 с вероятностью р
= 1 в выходную разность F(D) = 0.
Примеры таких характеристик для классической цепи Фестеля представлены на рис.
3. Более полный набор ДХ для фестелеобразных шифров приведен в работе [4].

Рис. 3
Важным
моментом следует считать также обнуляющие циклы, использующиеся в
характеристиках 1, 2 на рис. 3. Обнуление разности возможно, когда используются
сжимающие S-блоки. Примером может служить шифр DES, S-блоки которого определяют
закон отображения 6-битных значений в 4-битные. В этом случае нескольким
входным значениям может соответствовать одно выходное, т.е., имея на входе S-блока ненулевую разность, можно получить нулевую разность
на его выходе. Если обнулить таким образом все активные S-блоки
то будет получен обнуляющий цикл. В результате чередования тривиального и
обнуляющего циклов будет получена 2-цикловая итеративная дифференциальная
характеристика (ИДХ) обнуляющего типа (рис. 3,1), которая может быть повторена
нужное число раз для покрытия требуемого числа циклов.
Если в фестелеобразном шифре с разбиением на n
подблоков при прохождении через шифрующую функцию возможно обнуление разности,
то ДХ, в общем случае, может содержать n-1 тривиальных
циклов, прежде чем встретится обнуляющий цикл. На рис. 4 приведены ИДХ
обнуляющего типа, представляющие, по мнению многих ученых, наибольшую опасность
для шифров, построенных по схемам Фестеля.
Рис.
4
Для рассматриваемого фестелеобразного шифра с
шифрующей функцией, изображенной на рис. 2,б, граничное значение вероятности
r-цикловой ДХ, собранной из 2-цикловых характеристик обнуляющего типа, составит
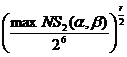 , a Î {0,1}6 (a ¹ 0), b Î {0,1}4. (2)
, a Î {0,1}6 (a ¹ 0), b Î {0,1}4. (2)
Дифференциальные
характеристики обнуляющего типа опасны еще и потому, что число активных S-блоков в циклах не зависит от рассеивающих качеств линейных
преобразований, так как на линейные преобразования всегда приходят нулевые
значения разности. Поэтому возможность реализации атак на основе
дифференциальных характеристик обнуляющего типа полностью определяется
свойствами нелинейных подстановок и, как показано в работах [4,5], опасность со
стороны таких ДХ может быть устранена путем предъявления дополнительных
требований
к этим подстановкам. В случае предъявления дополнительных требований к
подстановкам лучшей вероятностью будут обладать ДХ, общий вид которых приведен
на рис. 3,3. Граничное значение вероятности r-цикловой ДХ, собранной из
6-цикловых итеративных характеристик, составит
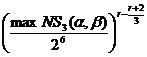 ,
a Î
{0,1}6 (a ¹ 0), b Î
{0,1}4. (3)
,
a Î
{0,1}6 (a ¹ 0), b Î
{0,1}4. (3)
Для фестелеобразного шифра, шифрующая функция
которого не содержит расширяюще-сжимающих преобразований (рис. 2,а), ДХ
обнуляющего типа нереализуемы. В этом случае лучшей вероятностью опять будут
обладать ДХ, общий вид которых приведен на рис. 3,3. Граничное значение
вероятности r-цикловой ДХ, собранной из 6-цикловых итеративных характеристик,
составит
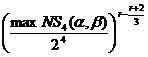 , a, b Î {0,1}4 (a ¹ 0). (4)
, a, b Î {0,1}4 (a ¹ 0). (4)
Из формул (1)-(4) видно, что для получения
окончательных значений необходимо учитывать дифференциальные свойства
используемых S-блоков. Будем ориентироваться на использование
подстановок с наименьшими максимальными значениями в дифференциальных таблицах.
Для биективных подстановок (в нашем случае для подстановок 4 в 4 бита) наиболее
удачными в этом смысле считаются преобразования с предельной нелинейностью (Almost Perfect Nonlinearity - APN),
которые рассматриваются в [7,8]. Максимальное значение в таблице
дифференциальной разности таких преобразований°– 4. Поэтому
принимаем max NS1(a,b) = max NS4(a,b) = 4. В шифрующей функции на рис. 2,б используется
небиективная подстановка 6 в 4 бита. Работы, в которых производилась бы оценка
дифференциальных свойств таких подстановок, нам не встретились. В результате
вычислительного эксперимента удалось построить подстановки, лучшая из которых
имеет максимальное значение в дифференциальной таблице, равное 10. Поэтому
предположим, что этот показатель может достичь значения 8 (max NS2(a,b) = 8).
Дополнительные требования, направленные на защиту от дифференциальных
характеристик обнуляющего типа, как показывает эксперимент, не оказывают
существенного влияния на минимаксное значение таблицы разностей. В ходе
вычислительного эксперимента нам удалось построить подстановку, которая, как и
в предыдущем случае, имеет максимальное значение в дифференциальной таблице,
равное 10. Опять, предположим, что этот показатель может быть улучшен до
значения 8 (max NS3(a,b) = 8).
Зависимости граничных вероятностей ДХ от
числа циклов r для рассматриваемых шифров представлены на рис. 5.
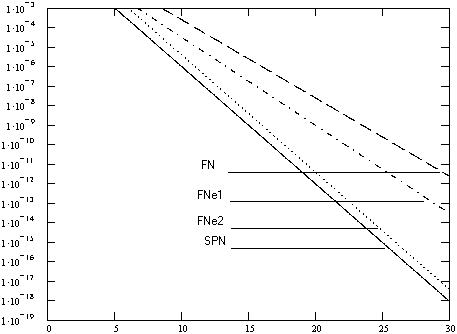
Рис.
5
Из графиков зависимостей видно, что если в качестве
операции рассеивания используются битовые перестановки, то при использовании
схемы Фестеля за равное число циклов может быть достигнут уровень стойкости,
обеспечиваемый SPN-схемой. Для этого необходимо использовать
расширяюще-сжимающую схему и накладывать на S-подстановки
ограничения на обнуление разности (FNe2). В противном случае (FNe1
– подстановки без ограничений на обнуление разности, FN – биективная
структура шифрующей функции) схема Фестеля уступает SPN-схеме по
стойкости на одинаковом числе циклов.
В современных шифрах в качестве операций рассеивания
вместо битовых перестановок используются линейные преобразования, преимущества
которых обсуждаются, например, в работе [9]. Среди линейных преобразований
широкое применение получили преобразования на основе МДР-кодов (коды с
максимально-допустимым расстоянием). Впервые такие преобразования были
использованы при построении блочного шифра Shark. Подобные
преобразования также используются в шифрах Square, Rijndael,
Khazad, Anubis. Главное
преимущество линейных преобразований этого класса заключается в том, что сумма
активных S-блоков в контексте дифференциального или линейного
криптоанализа до и после такого линейного преобразования будет максимально
возможным, т.е. равным M+1, где М – число S-блоков
покрываемых МДР-преобразованием.
Линейное преобразование на основе МДР-кодов обычно
задается в виде таблицы (матрицы), а реализуется путем умножения
информационного блока, представленного в виде вектора, на эту матрицу, причем
умножение отдельных элементов в целях более высокой скорости обычно
представляются в виде заранее просчитанных таблиц. Из этого следует, что
основной недостаток линейных МДР-преобразований заключается в том, что по мере
роста длины преобразуемого подблока растет время выполнения такого
преобразования, растет число таблиц умножения, а размер матрицы увеличивается
вдвое быстрее (2-кратное увеличение размера преобразуемого подблока влечет
4-кратное увеличение размера матрицы).
Рассмотрим, как в условиях использования в качестве
линейного уровня МДР-преобразований будут зависеть верхние границы вероятностей
дифференциальных характеристик от числа циклов для фестелеобразного и SPN-шифров
с размерами информационных блоков 2М слов (одно слово соответствует одному S-блоку).
В этом случае цикл фестель-подобного шифра будет содержать М S-блоков
и умножение подблока размером М слов на матрицу размером М´М слов. Для фестель-подобного шифра, по-прежнему
наибольшую опасность представляют характеристики обнуляющего типа, поскольку
улучшение линейного уровня не снижает их вероятность. Следовательно, этот вид
характеристик следует перекрыть в первую очередь. Как уже отмечалось ранее, это
может быть выполнено либо путем использования биективных подстановок, либо
путем предъявления дополнительных требований к сжимающим небиективным
подстановкам. В этих случаях наиболее опасными будут являться дифференциальные
характеристики, общий вид которых приведен на рис.3.3. В соответствии со
свойствами линейных преобразований на основе МДР-кодов число активных S-блоков
в каждых двух соседних нетривиальных циклах будет не менее, чем М+1, тогда
граничное значение вероятности r-цикловой ДХ, собранной из 6-цикловых
итеративных характеристик, составляет в первом случае:
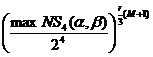 , a, b Î
{0,1}4 (a ¹ 0), (5)
, a, b Î
{0,1}4 (a ¹ 0), (5)
а во втором:
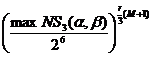 , a,
b Î {0,1}4 (a ¹ 0). (6)
, a,
b Î {0,1}4 (a ¹ 0). (6)
Если в SPN-шифре
использовать в качестве линейного преобразования умножение на матрицу 2М´2М слов, то такой шифр будет значительно медленнее,
чем описанный выше фестель-подобный. Примерно одинаковые показатели
быстродействия могут быть достигнуты, если линейное преобразование в SPN-шифре
выполнить как параллельное умножение половинок (колонок) размером М слов каждая
на матрицу М´М с последующей перестановкой слов между этими
половинками (аналогично линейным преобразованиям, применяющимся в шифре Rijndael
[10]). Исходя из того, что показатели рассеивания будут лучше, если при
перестановке слова каждой колонки распределяются поровну между всеми колонками
(в этом случае сложнее оставаться в рамках одной активной колонки) выбираем
именно такую перестановку (см. рис. 6).
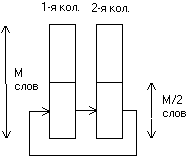
Рис. 6
Таким
образом, шифрующая функция SPN-шифра будет содержать 2М S-блоков, перестановку слов,
приведенную на рис. 6, умножение обоих колонок на матрицу размером М´М слов и, в заключение, сложение с подключом.
Аналогично методике, предложенной в шифре Rijndael [10], покажем, что любая
4-цикловая дифференциальная или линейная характеристика для такого шифра будет
содержать, по крайней мере, 3(М+1) активных S-блоков. Для этого введем следующие
обозначения: для i-го цикла ai-1
обозначает значение на входе перестановки слов между колонками, bi-1 –
значение после перестановки. Активной колонкой будем называть колонку, в
которой есть хотя бы один активный S-блок (активное слово).
Лемма 1. Для
рассматриваемого SPN-шифра число активных S-блоков в 2-цикловой линейной
или дифференциальной характеристике равно, по крайней мере, (М+1)×Q, где Q – число активных колонок на входе 2-го цикла.
Доказательство. Если в a1 какая-либо колонка активна, то аналогичная
колонка активна и в b0. Поскольку каждая колонка b0
проходит через умножение на МДР-матрицу, то сумма активных S-блоков в каждой
колонке b0 и соответствующей колонке a1
будет, по крайней мере, М+1. Таким образом, число активных S-блоков в b0
и a1 равно (М+1)×Q. Но,
поскольку b0 и a0 содержат равное число
активных S-блоков, то лемма доказана.
Лемма 2. Для
рассматриваемого SPN-шифра сумма активных колонок на входе и выходе любой
2-цикловой характеристики всегда будет не менее 3.
Доказательство. Если на входе 2 активные колонки, то с учетом того, что
дифференциальная разность всегда содержит хотя бы один активный S-блок,
а, значит, и одну активную колонку, т.е., в этом случае лемма справедлива.
Рассмотрим случай, когда на входе 1 активная колонка. Здесь возможно 2
варианта:
1. После операции перестановки слов между колонками
остается активной одна колонка.
В этом случае в a0 и b0
должны содержать менее чем M/2 активных слов в одной из колонок, тогда a1
в этой же колонке будет содержать, по крайней мере, М/2+1 активных слов. Отсюда
следует, что b1, а значит, и a2 будут
содержать две активные колонки.
2. После операции перестановки слов между колонками
активны две колонки.
В этом случае b0 будет содержать не
более М/2 активных слов в каждой из двух колонок, а a1,
соответственно, - по крайней мере, М/2+1 активных слов в каждой
колонке. Но тогда b1 содержит, по крайней мере
(М/2+1)+(М/2+1)=М+2 активных слова, следовательно, активны обе колонки.
Лемма доказана.
Теорема 1. Для
рассматриваемого SPN-шифра каждая дифференциальная или линейная 4-цикловая
характеристика содержит, по крайней мере, 3×(М+1) активных
слова.
Доказательство. Применяя лемму 1 к первым двум циклам (1 и 2) и ко вторым двум (3 и 4)
получаем, что минимальное число активных слов в четырех циклах равно сумме
активных колонок в a1 и a3, умноженной на
(М+1). А из леммы 2 следует, что эта сумма составит, по крайней мере, 3.
Теорема доказана.
Учитывая теорему 1, граничное значение вероятности
r-цикловой ДХ будет составлять
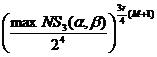 , a,
b Î {0,1}4 (a ¹ 0). (7)
, a,
b Î {0,1}4 (a ¹ 0). (7)
Для рассматриваемых ранее шифров М = 2. Зависимости
граничных вероятностей ДХ от числа циклов r для
шифров, использующих МДР-преобразования, представлена на рис. 7.
Из приведенных графиков видно, что, при использовании
в шифрах более хороших процедур рассеивания, чем битовые перестановки, схемы
Фестеля (FNe и FN) уступают SPN-схеме по стойкости к атакам
ДК. Так, схема Фестеля с расширяюще-сжимающими преобразованиями для достижения
стойкости, обеспечиваемой SPN схемой, требует примерно в 1,5 раза больше циклов, а
схема Фестеля с биективными преобразованиями – примерно в 2,2 раза.
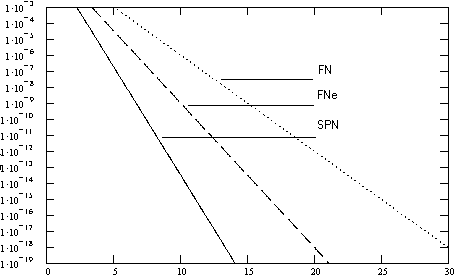
Рис.
7
Таким образом, в ходе исследований были предложены
способы выполнения оценки стойкости различных шифров к дифференциальным атакам.
Показано, что для фестель-подобных шифров, с точки зрения обеспечения стойкости
к дифференциальному криптоанализу, эффективно использование
расширяюще-сжимающих преобразований, хотя они менее удобны в реализации. Их
применение, при использовании в качестве линейных преобразований битовых
перестановок, позволяет фестель-подобному шифру достигнуть уровня стойкости,
обеспечиваемого SPN-схемой с тем же числом циклов. Однако, при
использовании в качестве операций рассеивания более сложных линейных
преобразований, чем битовые перестановки, уровень стойкости, обеспечиваемый SPN-шифром,
не достижим для фестель-подобного шифра с тем же числом циклов. Следовательно,
вопросы защищенности фестель-подобного шифра от атак ДК в этом случае требуют
большего внимания. Обычно эти вопросы решаются либо путем введения
дополнительных операций (см. [11,12]), либо путем увеличения числа циклов шифрования,
что в любом случае влечет за собой снижение скорости – важнейшей характеристики
для симметричных блочных шифров.
Литература: 1. National Bureau of
Standards, Data Encryption Standard, U.S. Department of Commerce, FIPS pub. 46,
January 1977. 2. E. Biham, A. Shamir. Differential Cryptanalysis of the
DES- like Cryptosystems, Journal of Cryptology. Vol. 4. P. 3-72. 1991. 3.
E. Biham, A. Shamir. Differential Cryptoanalysis of the full 16-round
DES // Technical Report. Computer Science Department. Technion. Israiel. 1993.
4. Долгов В.И., Лисицкая И.В., Руженцев В.И. Обеспечение стойкости шифра DES к атакам дифференциального криптоанализа. Перекрытие итеративных характеристик обнуляющего типа и
четырехцикловых итеративных характеристик // Радиотехника. 2001. № 120. С.
192-198. 5. Бондаренко М.Ф., Коряк А.С., Руженцев В.И. Повышение
устойчивости шифра DES к атакам дифференциального криптоанализа //
Радиотехника: Всеукр. межвед. науч.-техн.сб. 2001. № 119. С. 172-176. 6. Долгов
В.И. Лисицкая И.В., Головашич С.А. Принципы защиты алгоритма DES от атак дифференциального криптоанализа // Радиотехника:
Всеукр. межвед. науч.-техн.сб. 2000. № 113. С. 148-157. 7. T. Beth, C. Ding. On Almost Perfect Nonlinear
Permutation // Springer Verlag, Berlin. 1993. 8. K. Nyberg.
Differentially uniform mappings for cryptography // Advances in Cryptology, Proceedings Eurocrypt'93, LNCS 765, T. Helleseth,
Ed., Springer-Verlag, 1994, pp. 55-64. 9. H.M. Heys, S.E. Tavares. The
design of product ciphers resistant to differential and linear cryptanalysis //
Journal of cryptology, Vol. 9, no. 1, pp. 1-19, 1996. 10. J. Daemen, V. Rijmen. AES Proposal Rijndael, AES
Round 1 Technical Evaluation CD1: Documentation, National Institute of
Standards and Technology, Aug 1998. See http://www.nist.gov/aes. 11. Пат. 42531А Украина, H04L9/06. Способ шифрования данных
для систем обработки в ЭВМ / Долгов В.И., Лисицкая И.В.
и др.; №2001032062; Заявл. 28.03.2001; Опубл. 15.10.2001.
12. Долгов в.и.,
Руженцев В.И., Федотов М.А. MDES-128 с таблицами подстановок случайного типа //
Радиотехника: Всеукр. межвед. науч.-техн.сб. 2001. № 119. С. 166-171.
Харьковский
национальный университет радиоэлектроники Поступила в
редколлегию 25.04.2002


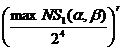 ,
a, b Î
{0,1}4 (a ¹ 0), (1)
,
a, b Î
{0,1}4 (a ¹ 0), (1)
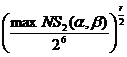
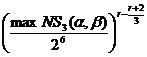 ,
,
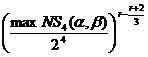

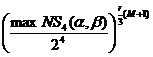 ,
, 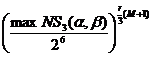 ,
, 
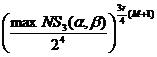 ,
, 