|
Быстрый поиск по дереву суффиксов
Марк Нельсон
Dr. Dobb's Journal Август 1996
Быстрый поиск по дереву суффиксов
Я думаю, что я никогда не буду видеть
Поэмы прекрасной как дерево.
Поэмы это сочетания
сделанные дураками подобно мне,
Но только Бог может делать дерево.
Джойс Килмер
Дерево дерева. Насколько выше Вы должны смотреть?
Рональд Рейган
Соответствие строковым последовательностям - проблема, с которой компьютерные программисты сталкиваются на правильном основании. Некоторые задачи программирования, типа сжатия данных или ДНК последовательности, могут извлечь выгоду чрезвычайно из усовершенствований строки, соответствующей алгоритмам. Эта статья обсуждает относительно неизвестную структуру данных, дерево суффикса, и показывает, как его характеристики могут использоваться, чтобы напасть на трудную строку, соответствующую проблемам.
Проблема
Вообразите, что Вы были только что наняты как программист, работающий над проектом ДНК последовательности. Исследователи заняты, разрезая и исследуя вирусный генетический материал, производя фрагментированные последовательности нуклеотидов. Они посылают эти последовательности вашему серверу, который, как ожидается, определит местонахождение последовательностей в базе данных геномов. Геном для данного вируса может иметь сотни тысяч оснований нуклеотида, и Вы имеете сотни вирусов в вашей базе данных. Вы, как ожидается, осуществят это как клиент-серверный проект, который дает обратную связь в реальном масштабе времени нетерпеливому Ph. D.s. В чем состоит лучший путь?
В этом пункте очевидно, что поиск строки решения "в лоб" собирается быть ужасно неэффективным. Этот тип поиска требовал бы, чтобы Вы исполнили строковое сравнение в каждом отдельном нуклеотиде в каждом геноме в вашей базе данных. Испытание длинного фрагмента, который имеет высокую степень совпадения частичных пар, заставило бы вашу клиент-серверную систему напомнить старинную машину пакетной обработки. Ваш вызов должен прибыть с эффективной строкой, соответствующей решению.
Интуитивное решение
Так как база данных, против которой Вы проверяете, является инвариантной, предварительная обработка, это, чтобы упростить поиск походит на хорошую идею. Один подход предварительной обработки состоит в том, чтобы формировать TRIE-структуру поиска. Для того, чтобы перерывать входной текст, прямой подход к TRIE-структуре поиска приводит к вещи названной TRIE-структурой суффикса. (TRIE-структура суффикса - только один шаг далекий от моего конечного адресата, дерева суффикса.) TRIE-структура - тип дерева, которое имеет N возможные ветви от каждого узла, где N - число символов в алфавите. Слово 'суффикс' используется в этом случае, чтобы обратиться к факту, что TRIE-структура содержит все суффиксы данного блока текста (возможно вирусный геном.)
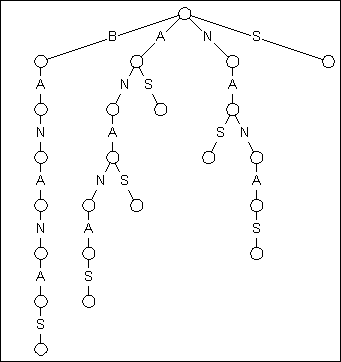
Рисунок 1
TRIE-структура Суффикса, представляющая "BANANAS"
Рисунок 1 показывает TRIE-структуре Суффикса для слова BANANAS. Есть два важных факта, чтобы обратить внимание об этой TRIE-структуре. Сначала, начинающийся в корневом узле, каждый из суффиксов BANANAS найден в TRIE-структуре, начинающейся с BANANAS, ANANAS, NANAS, и заканчивающийся с уединенным S. Во вторых, из-за этой организации, Вы можете искать любую подстроку слова, начинаясь в корне и после пар вниз дерево пока не истощено.
Второй пункт - то, что делает TRIE-структуру суффикса такой хорошей конструкцией. Если Вы имеете входной текст длины N, и строки для поиска длины M, традициональный поиск решения "в лоб" возьмет столько, сколько сравнение символа N*M, чтобы завершить. Оптимизированные ищущие методы, типа Boyer-Moore алгоритма могут гарантировать исследования, это требует не больше, чем M+N сравнений, с четным лучше составляют в среднем работу{выполнение}. Но TRIE-структура суффикса упрощает эту работу, требуя только сравнений символа M, независимо от длины обыскиваемого текста!
Замечательный, поскольку это могло бы казаться, это означает, что я мог определить, было ли слово BANANAS в собрании сочинений Уильяма Шекспира, выполняя только семь символьных сравнений! Конечно, есть только один небольшой арретир: время на создание TRIE-структуры.
Причина, которую Вы не понимаете об использовании попыток суффикса - простой факт, что построение того требует O (N2) время. Эта квадратичная работа исключает использование попыток суффикса, где они необходимы больше всего: перерывать длинные блоки данных.
Под распространяющимся деревом суффикса
Разумный путь мимо этой дилеммы был предложен Эдвардом Маккритом в 1976, когда он издал его бумагу в которой говорилось о том, что впоследствии стало известным как дерево суффикса. Дерево суффикса для данного блока данных сохраняет ту же самую топологию как TRIE-структура суффикса, но это устраняет узлы, которые имеют только единственного потомка. Этот процесс, известный как сжатие пути, означает, что индивидуальные грани в дереве теперь могут представить последовательности текста вместо единственных{отдельных} символов.
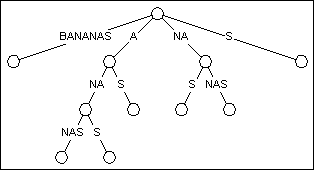
Рисунок 2
Дерево суффикса представление BANANAS
Рисунок 2 показывает тому, что TRIE-структура суффикса от Рисунка 1 напоминает преобразованное дерево суффикса. Вы можете видеть, что дерево все еще имеет ту же самую общую форму, только гораздо меньше узлов. Устраняя каждый узел с только единственным потомком, граф уменьшен от 23 до 11.
Фактически, сокращение номера узлов - такой, что время и пространственные требования чтобы создавать дерево суффикса уменьшены от O (N2) к O (N). В самом плохом случае, дерево суффикса может быть сформировано с максимумом 2N узлы, где N - длина входного текста. Так для одноразовых вхождений, пропорциональных длине входного текста, мы можем создать дерево, которое наша строка ищет.
Даже Вы можете создать дерево
Первоначальный алгоритм Маккрита чтобы создать дерево суффикса имел несколько недостатков. Требование, чтобы дерево было с обратным порядком, означающие символы добавился с конца ввода. Это исключило алгоритм для обработки строки, другой аналогичный алгоритм только более трудный используется для приложений типа сжатия данных.
Двадцать лет спустя, Эско Укконен от Университета Хельсинки прибыл в разработал немного изменяемую версию алгоритма, который работает слева направо. И мой типовой код и описания, которые следуют, основаны на работе Укконена, издал в выпуске за сентябрь 1995 Algorithmica..
Для данной строки текста, T, алгоритм Укконена начинается с пустым деревом, тогда прогрессивно добавляет каждый из N префиксов T к дереву суффикса. Например, при создании дерева суффикса для BANANAS, B вставлен в дерево, тогда BA, затем BAN, и так далее. Когда BANANAS наконец вставлены, дерево закончено.
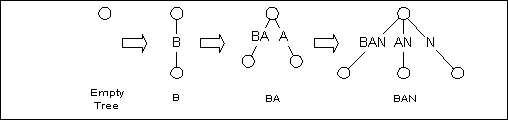
Рисунок 3
Прогрессивное формирование дерева суффикса
Механизм суффиксного дерева
Добавление нового префикса к дереву сделано, идя через дерево и посещая каждый из суффиксов текущего дерева. Мы запускаем в самом длинном суффиксе (BAN в Рисунке 3), и работе наш путь вниз к самому короткому суффиксу, который является пустой строкой. Каждый суффикс заканчивается в узле, который состоит из одного из этих трех, напечатает:
- Вершина. В Рисунке 4, узлы маркировали 1,2, 4, и 5 - вершины.
- Явный узел. Невершины, которые помечены 0 и 3 в Рисунке 4 - явные узлы. Они представляют точку на дереве где две или больше части граней пути.
- Неявный узел. На Рисунке 4, префиксы типа BO, BOO, и OO весь конец в середине края. Эти позиции упоминаются как неявные узлы. Они представили бы узлы в TRIE-структуре суффикса, но сжатие пути устранило их. Поскольку дерево сформировано, неявные узлы иногда преобразовываются в явные узлы.
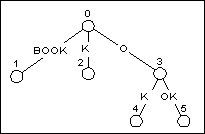
Рисунок 4
BOOKKEEPER после добавления BOOK
В Рисунке 4, есть пять суффиксов в дереве (включая пустую строку) после добавления BOOK к структуре. Добавляя следующий префикс, BOOKK к дереву означает посещать каждый из суффиксов в существующем дереве, и добавлении символа K до конца суффикса.
Первые четыре суффикса, BOOK, OOK, OK, и K, в вершинах.
После того, как все вершины были модифицированы, мы все еще должны добавлять 'K' символа к пустой строке, которая найдена в узле 0. Так как есть уже край, оставляющий узел 0, который начинается с символом K, мы не должны сделать ничего. Недавно добавленный суффикс K будет найден в узле 0, и закончится в неявном узле, нашел один символ вниз по краю, ведущему к узлу 2.
Конечную форму заканчивающегося дерева показано на Рисунке 5.
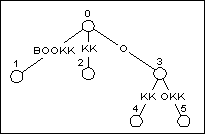
Рисунок 5
То же самое дерево после добавления BOOKK
Это становится затруднительным
Модифицирование дерева на Рисунке 4 было относительно просто. Мы выполнили два типа обновлений: первый было просто расширение края, и второй было неявное обновление. Добавление BOOKKE к дереву, показанному на Рисунке 5 будет демонстрировать два других типа обновлений. В первом типе, новый узел создан, чтобы разбить существующий край в неявном узле, сопровождаемом добавлением нового края. Второй тип обновления состоит из добавления нового края к явному узлу.

Рисунок 6
Разбиение и Добавление обновления
При добавлении BOOKKE к дереву на Рисунке 5, мы еще раз запускаем с самого длинного суффикса, BOOKK, и работы наш путь к самому короткому, пустая строка. Модифицирование более длинных суффиксов тривиально, пока мы модифицируем вершины. На Рисунке 5, суффиксы, которые заканчиваются в вершинах - BOOKK, OOKK, OKK, и KK. Первое дерево на Рисунке 6 показывает тому, что дерево напоминает после того, как они прибавляют, были модифицированы, используя простое строковое расширение.
Первый суффикс на Рисунке 5, которое не заканчивается в вершине - K. При модифицировании дерева суффикса, первая невершина определена как активная точка дерева. Все суффиксы, которые более длинны чем суффикс, определенный активной точкой, закончатся в вершинах. Ни один из суффиксов после этой точки не закончится в вершинах.
Суффикс K заканчивает в неявной части узла путь вниз край, определенный KKE. При испытании невершин, мы должны видеть, имеют ли они любых потомков, которые соответствуют новому добавляемому в конец символу. В этом случае, который был бы E.
Быстрый взгляд на первый K на показах KKE, что это только имеет единственного потомка: K. Так что это означает, что мы должны добавить потомка, чтобы представить Письмо E. Это - два процесса шага. Сначала, мы разбиваем край, проводя дугу так, чтобы это имело явный узел в конце проверяемого суффикса. Среднее дерево на Рисунке 6 показывает тому, что дерево напоминает после разбиения.
Как только край был разбит, и новый узел добавился, Вы имеете дерево, которое напоминает это в третьей позиции Рисунка 6. Обратите внимание, что K узел, который теперь рос, чтобы быть KE, стал вершиной.
Модифицирование явного узла
После модифицирования суффикса K, мы все еще должны модифицировать следующий, короче прибавляют, который является пустой строкой. Пустая строка заканчивается в явном узле 0, так что мы только должны выяснить, если это имеет потомка, который начинается с символом E. Быстрый взгляд на дерево на Рисунке 6 показывает тому узлу 0, не имеет потомка, так что другая вершина добавляется, который приводит к дереву, показанному на Рисунке 7.
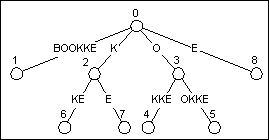
Рисунок 7
Обобщение алгоритма
Используя в своих интересах несколько из характеристик дерева суффикса, мы можем генерировать довольно эффективный алгоритм. Первая важная черта - это: однажды вершина, всегда вершина. Любому узлу, который мы создаем как лист, никогда не будут давать потомка, это будет только расширено через символьную конкатенацию. Что еще более важно, каждый раз, когда мы добавляем новый суффикс к дереву, мы собираемся автоматически расширять грани, вводящие в каждую вершину единственным символом. Тот символ будет последним символом в новом суффиксе.
Это делает управление граней, вводящих в простые вершины. В любое время мы создаем новую вершину, мы автоматически, устанавливает ее край представлять все символы от ее отправной точки до конца входного текста. Даже если мы не знаем, каковы те символы, мы знаем, что они будут добавляться к дереву в конечном счете. Из-за этого, как только вершина создана, мы можем только забыть об этом! Если край разбит, его отправная точка может измениться, но это будет все еще простираться полностью до конца входного текста.
Это означает, что мы только должны волноваться о модифицировании явных и неявных узлов в активной точке, который был первой невершиной. Учитывая это, мы должны были бы прогрессировать от активной точки до пустой строки, проверяя каждый узел для преемственности обновления.
Однако, мы можем экономить некоторое время, останавливая наше обновление ранее. Поскольку мы идем через суффиксы, мы добавим новый край к каждому узлу, который не имеет порожденного края, начинающегося с правильного символа. Когда мы наконец достигаем узла, который имеет правильный символ как потомок, мы можем просто прекратить модифицировать. Зная, как работы алгоритма конструкции, Вы могут видеть что, если Вы находите некоторый символ как потомок специфического суффикса, Вы связаны также найти это как потомок каждого меньшего суффикса
Точку, где Вы находите первого потомка соответствия, называют конечной точкой. Конечная пункт имеет дополнительную особенность, которая делает это особенно полезным. С тех пор как мы добавляли листья к каждому суффиксу между активной точкой и конечной точкой, мы теперь знаем, что каждый суффикс дольше чем конечная точка - вершина. Это означает, что конечная точка превратится в активную точку на следующем, передают по дереву!
В заключении наших обновлений к суффиксам между активной точкой и конечной точкой, мы урезаем путь на обработке, требуемой модифицировать дерево. И следя за конечной точкой, мы автоматически знаем то, чем активная точка будет на следующем проходе. Первый проход в алгоритме обновления, используя эту информацию мог бы смотреть кое-что подобно этому (в C-like псевдо коде): Update( new_suffix )
{
current_suffix = active_point
test_char = last_char in new_suffix
done = false;
while ( !done ) {
if current_suffix ends at an explicit node {
if the node has no descendant edge starting with test_char
create new leaf edge starting at the explicit node
else
done = true;
} else {
if the implicit node's next char isn't test_char {
split the edge at the implicit node
create new leaf edge starting at the split in the edge
} else
done = true;
}
if current_suffix is the empty string
done = true;
else
current_suffix = next_smaller_suffix( current_suffix )
}
active_point = current_suffix
}
Указатель на суффикс
Алгоритм псевдокода, показанный выше более или менее точен, но это заминает одну трудность. Поскольку мы перемещаемся через дерево, мы двигаемся в следующий меньший суффикс через запрос к next_smaller_suffix (). Эта подпрограмма должна найти неявный или явный узел, соответствующий специфическому суффиксу.
Если мы делаем это, просто спускаясь с дерева, пока мы не находим правильный узел, наш алгоритм не собирается работать в линейном времени. Чтобы обойти это, мы должны добавить один дополнительный указатель на дерево: указатель суффикса. Указатель суффикса - указатель, найденный в каждом внутреннем узле. Каждый внутренний узел представляет последовательность символов, которые начинаются в корне. Указатель суффикса указывает на узел, который является первым суффиксом той строки. Так, если специфическая строка содержит, символы 0 через N входного текста, указатель суффикса для той строки укажут на узел, который является точкой завершения для строки, начинающейся в корне, который представляет символы 1 через N входного текста.
Рисунок 8 показывает дереву суффикса для строки ABABABC. Первый указатель суффикса найден в узле, который представляет ABAB. Первым суффиксом той строки была бы BAB, и это - то, где указатель суффикса в ABAB указывает. Аналогично, BAB имеет его собственный указатель суффикса, который указывает на узел для AB.
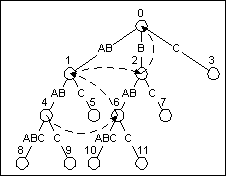
Рисунок 8
Дерево суффикса для ABABABC с указателями суффикса показанны штриховой линией
Указатели суффикса сформированы, в то же самое время когда обновление к дереву имеет место. Поскольку я двигаюсь от активной точки, до конца указывают, я слежу за родительской вершиной каждого из новых листьев, которые я создаю. Каждый раз, когда я создаю новый лист, я также создаю указатель суффикса от родительской вершины последнего края листа, который я создавал к текущему родительскому листу. (Очевидно, я не могу сделать этого для первого листа, созданного в обновлении, но я делаю для всех остающихся граней.)
С указателями суффикса на месте, перемещаясь от одного суффикса до следующего - просто вопрос следующих указатель. Это критическое добавление к алгоритму - то, что уменьшает это до O (N) алгоритм.
Дома дерева
Чтобы помогать иллюстрировать эту статью, я записал короткую программу, STREE.CPP, который читает в строке текста от стандартного ввода и формирует дерево суффикса. Версия, показанная в Распечатке 1, является полностью зарегистрированным C++. Вторая версия, STREED.CPP, имеет обширный вывод отладки также, и доступна от DDJ, печатающего службу, так же как мою домашнюю страницу.
Понимание STREE.CPP - действительно только вопрос понимания работ структур данных, которые это содержит. Самая важная структура данных - объект Edge. Определение класса для диста: class Edge {
public :
int first_char_index;
int last_char_index;
int end_node;
int start_node;
void Insert();
void Remove();
Edge();
Edge( int init_first_char_index,
int init_last_char_index,
int parent_node );
int SplitEdge( Suffix &s );
static Edge Find( int node, int c );
static int Hash( int node, int c );
};
Каждый раз, когда новый край в дереве суффикса создан, новый объект Edge создан, чтобы представить это. Четыре компонента данных объекта определены следующим образом:
| first_char_index, last_char_index: |
Каждая из граней в дереве имеет последовательность символов от входного текста, связанного с этим. Чтобы гарантировать, что размер памяти каждого края является идентичным, мы только сохраняем два индекса во входной текст, чтобы представить последовательность.
|
| start_node: |
Номер узла, который представляет стартовый узел для этого края. Узел 0 - корень дерева. |
| end_node: |
Номер узла, который представляет конечный узел для этого края. Каждый раз, когда край создан, новый конечный узел создан также. Конечный узел для каждого края не будет переключать жизнь дерева, так что это может использоваться как идентификатор края также.
|
Одна из самых частых задач выполнила, когда формирование дерева суффикса должно искать край, происходящий от специфического узла, основанного на первом символе в его последовательности. На байте ориентировал компьютер, могли быть целых 256 граней, происходящих в отдельном узле. Чтобы делать поиск разумно быстрым и простым, я сохраняю грани в хеш-таблице, используя ключ мусора, основанную на их стартовом номере узла и первом символе их подстроки. Вставка () и Удаляет (), функции члена используются, чтобы управлять передачей граней в и из хеш-таблицы.
Вторая важная структура данных, используемая при формировании дерева суффикса - объект Suffix. Помните, что модифицирование дерева сделано, работая через все суффиксы строки, в настоящее время сохраненной в дереве, начинаясь с самого длинного, и заканчиваясь в конечной точке. Суффикс - просто последовательность символов, которая начинается в узле 0 и концах в некоторый момент в дереве.
Это имеет смысл, что мы можем тогда безопасно представить любой суффикс, определяя только позицию в дереве ее последнего символа, так как мы знаем первые символьные запуски в узле 0, корне. Объект Suffix, определение которого показывают здесь, определяет данный суффикс, используя ту систему: class Suffix {
public :
int origin_node;
int first_char_index;
int last_char_index;
Suffix( int node, int start, int stop );
int Explicit();
int Implicit();
void Canonize();
};
Объект Suffix определяет последний символ в строке, начинаясь в определенном узле, тогда после строки символов во входной последовательности, на которую указывает first_char_index и last_char_index члены. Например, на Рисунке 8, самый длинный суффикс "ABABABC" имел бы origin_node 0, first_char_index 0, и last_char_index 6.
Алгоритм Укконена требует, чтобы мы работали с этими определениями Суффикса каноническую форму. Канонизирующийся () функцию вызывают, чтобы исполнить это преобразование любое время, объект Suffix изменяется. Каноническое представление суффикса просто требует, чтобы origin_node в объекте{цели} Suffix были самый близкий родитель до конца точка строки. Это означает, что строка суффикса, представленная парой (0, "ABABABC"), канонизировалась бы, перемещая сначала в (1, "ABABC"), тогда (4, "ABC"), и наконец (8, " ").
Когда строка суффикса заканчивается на явном узле, каноническое представление будет использовать пустую строку, чтобы определить символы сохранения в строке. Пустая строка определена, устанавливая быть больше чем last_char_index. Когда дело обстоит так, мы знаем, что суффикс заканчивается на явном узле. Если first_char_index меньше чем или равен last_char_index, это означает, что строка суффикса заканчивается на неявном узле.
Учитывая эти данные структурируют определения, я думаю, что Вы найдете код в STREE.CPP, чтобы быть прямым выполнением алгоритма Укконена. Для дополнительной ясности, используйте STREED.CPP, чтобы формировать дамп обильной информации отладки во время выполнения.
Благодарность
Я был наконец убежден, чтобы заняться конструкцией дерева суффикса, читая доклад Джеспера Ларссона для 1996 Конференции Сжатия Данных IEEE. Джеспер был также достаточно любезен, чтобы обеспечить меня типовым кодом и указателями на доклад Укконена.
Ссылки
E.M. McCreight. Пространствено-экономичный алгоритм конструкции дерева суффикса. Журнал ACM, 23:262-272, 1976.
E. Укконен. Сетевая конструкция деревьев суффикса. Algorithmica, 14 (3):249-260, сентябрь 1995.
Наверх
|


