| Назад | На главную |
Борщевский С.В., Левит В.В., Сирачев А.Ж., ДНТУ, Украина, Прокопова М.Ю., Шахтинский институт ЮРГТУ, Россия
УДК 622.258
Источник: ТОВ "Технопарк ДонНТУ" "УНІТЕХ", Донецк 2006 г. III науково-практична конференція "ДОНБАС-2020: НАУКА І ТЕХНІКА - ВИРОБНИЦТВУ"
На базі натурних спостережень і аналізу журналів проходки і журналів кріплення 109 вертикальних стволів вугільних шахт Донбасу зроблені які-сна і кількісна оцінки стану вибоїв, виявлені фактори, що впливають на формування бетонного кріплення вертикальних стволів, розроблена графічна і чисельна реалізація розрахунків напряженно-деформованого стану кріплення стволів на кінцево-елементних моделях.
Вертикальные шахтные стволы,отличаясь своей уникальностью и важностью в производственном комплексе горнодобывающего предприятия, требуют постоянного поиска и разработки эффективных решений по интенсификации их строительства и безремонтной эксплуатации [1], что в свою очередь является актуальной научно-технической проблемой развития угольной промышленности Украины.
На нынешнем этапе изучения условий эксплуатации Донецкого угольного бассейна накоплены весомые знания об особенностях проявления горного давления в подземных выработках, в т.ч. и в вертикальных стволах. В условиях Донбасса выделяют следующие геомеханические особенности породного массива [2]:
Для облегчения выбора технологии проходки вертикальных стволов и обоснования способов крепления [3] в условиях различных водопритоков, авторами были подвергнуты обработке статистические данные из журналов проходки (рис.1) с учетом горно-геологических характеристик породного массива, толщины и вида крепи, темпов проходки по 109 стволам Донбасса, различного диаметра и глубины. Обработанные данные показали (рис.2), что в качестве крепи вертикальных стволов наиболее широкое распространение получила бетонная крепь класса В 15…25 по прочности и толщиной 300…500 мм.
А также было выявлено, что с увеличением глубины и диаметра ствола усиливается отклонение формы крепи от проектной, т.е. крепь становится не круговым кольцом, а приобретает форму, внешний контур которой представляет собой окружность, а внутренний (в результате деформации опалубки) – овал (близкий к эллипсу), при этом их центры могут не совпадать в силу возможного отклонения центрального отвеса при установке опалубки. Все это приводит к формированию кольца крепи переменной толщины, которая в зависимости от глубины и диаметра изменяется в пределах от 48,8% до 148,5% от проектной. В связи с этим максимальные напряжения и деформации в местах ее максимального утонения увеличиваются, а несущая способность крепи снижается.
Отсюда логически была поставлена и решена одна из задач исследований - изучение изменения напряженно-деформированного состояния (НДС) крепи в результате изменения формы и положения ее внутреннего контура и установление зависимости увеличения максимальных напряжений и деформаций крепи относительно исходных (при проектном положении опалубки) от глубины и диаметра ствола.
Для решения поставленной задачи использовался метод конечных элементов (МКЭ), реализованный в форме перемещений [4]. Для численного моделирования по этому методу используем программный комплекс «ЛИРА-Windows» (версия 8.01) [5]. Для расчета величин нагрузок написана программа NAGRUZ на языке QuickBasic 4.5.
Реализованный вариант МКЭ использует принцип возможных перемещений
a(u, v) =(f, v) (1)
где u – искомое точное решение; v – любое возможное перемещение; a(u, v), (f, v) – возможные работы внутренних и внешних сил.
Занимаемая конструкцией крепи область разбивается на конечные элементы Степеням свободы соответствуют базисные (координатные, аппроксимирующие) функции Приближенное значение Uh ищется в виде линейной комбинации базисных функций, удовлетворяющей главным (кинетическим) условиям
где ui – числа, N – количество степеней свободы.
Подставляя в (1) Uh вместо U и Обозначив через К матрицу жесткости с элементами
KX = P. (5)
Таким образом, применение МКЭ сводит задачу к системе линейных алгебраи-ческих уравнений (5). Решив ее, находим вектор Х, затем из (3) – остальные компоненты напряженно-деформированного состояния (НДС).
Так как крепь ствола работает совместно с вмещающим породным массивом, для изучения возникающего при этом НДС моделируем породный массив, в центре которого расположено круглое отверстие (моделирующее сечение ствола), ограниченное по контуру конечными элементами, моделирующими бетонную крепь.
Так как производится исследование изменения НДС от смещения внутреннего контура крепи и изменения формы поперечного сечения, постановки объемной задачи не требуется, поэтому ставится плоская задача с использованием для моделирования массива универсальных прямоугольных (рис. 3, а), а для моделирования крепи, в соответствии с рекомендациями [6], – универсальных треугольных (рис. 3, б) конечных элементов пластины с заданными жесткостными характеристиками.
В отличие от базовых моделей, задающих бетонное кольцо постоянной толщины, в моделях II группы внутренний контур крепи выполнен в виде эллипсов, большая полуось и эксцентриситет которых рассчитаны в зависимости от глубины и диаметра ствола по программе «Эллипс» [7].
Для оценки изменения НДС крепи ствола в результате изменения ее формы и возможного смещения опалубки были рассчитаны перемещения узлов и эквивалентные напряжения в конечных элементах моделей.
Пример разработанной конечно-элементной модели для расчета параметров базового НДС представлен на рис. 4 (модель для ствола диаметром в свету 6 м и толщиной крепи 250 мм, работающей под нагрузкой, рассчитанной для глубины 1200 м).
Пример конечно-элементной модели, характеризующей напряженно-деформированное состояние крепи с отклонениями формы и толщины от проекта, приведен на рис. 5 (модель для ствола диаметром в проходке 6,5 м, с переменной толщи-ной крепи, вследствие допустимого смещения и эллиптичности опалубки с соотношением полуосей эллипса 0,947, работающей под той же нагрузкой).
Расчет параметров НДС для моделей I группы производился с целью определения базовых смещений и напряжений, возникающих в крепи при строгом соблюдении технологии проходки и крепления ствола (кольцо постоянной толщины с центром, сов-падающим с центром ствола). Расчет параметров критического НДС на моделях II группы производился для оценки изменения величин смещений узлов и напряжений в элементах модели относительно базового НДС, вследствие образования кольца крепи переменной толщины из-за технологических погрешностей крепления ствола (рис.5).
На каждой из 48 моделей исследовано НДС крепи и массива для 3 различных типов вмещающих пород: крепких, средней крепости и слабых и монолитной крепи из бетона класса В25. Принятые в моделях жесткостные характеристики конечных элементов приведены в табл. 1.
Таблица 1 - Механические характеристики моделируемых материалов [6]
Выводы.
Литература


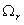 , назначаются узлы и их степени свободы
, назначаются узлы и их степени свободы 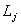 (перемещения и углы поворота узлов).
(перемещения и углы поворота узлов).
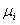 , отличные от нуля только на соответствующих звездах элементов и удовлетворяющие равенствам
, отличные от нуля только на соответствующих звездах элементов и удовлетворяющие равенствам
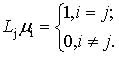 (2)
(2)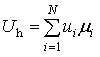 (3)
(3)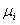 (j = 1,…N) вместо v, получим систему МКЭ
(j = 1,…N) вместо v, получим систему МКЭ
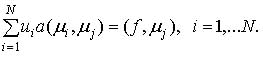 (4)
(4)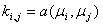 , P – вектор нагрузок с элементами
, P – вектор нагрузок с элементами 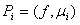 и X – искомый вектор с элементами
и X – искомый вектор с элементами  , запишем систему (4) в матричной форме
, запишем систему (4) в матричной форме




Назад
На главную