A GENETIC ALGORITHM
Harold Brochmann
Numerical problem solving techniques used with computers can be characterized as being either deterministic or non-deterministic. Deterministic procedures are the most familiar and they are employed when there is only one, or a limited number of 'right answers' which are a known function of available data. For example, the answers to many engineering problems are obtained by substituting empirically obtained measurements into standard formulas. Computers are not really essential for such problem solving procedures. Calculators can also be used. Writing computer programs that do this sort of thing involves writing algorithms that describe the desired functions. It's usually pretty straight forward stuff.Many problems do not have solution sets clearly defined by known functions; the solution algorithm may not have been worked out, or it may not exist. Consider The Travelling Salesman Problem which involves finding the most efficient route to be followed by a salesperson who wants to visit some number of cities. One approach is to calculate the length of all possible routes. The difficulty here is that as the number of places to visit increases, the number of possible routes becomes so large that the time taken for a computer to evaluate them all becomes impractical.
One technique for solving such problems involves generating and evaluating a large number of random solutions, and then selecting the best of those generated. It can be demonstrated that such proposed solutions differ from the ideal by so little that there are no practical advantage in pursuing the matter further. Such stochastic procedures find solutions as opposed to determine them.
An improvement on such methods is to create efficient algorithms that generate 'better suggestions' on the basis of results obtained so far in order to reduce the trial and error component.
Genetic Algorithms are computer procedures that employ the mechanics of natural selection and natural genetics to 'evolve' solutions to problems. The purpose of this article is to explain, through a specific example, the general structure of such algorithms. The example is an adaptation of a computer program described in the third chapter of the book Genetic Algorithms in Search, Optimization
&Machine Learning by David E Goldberg (Addison-Wesley, 1989).The chromosomes found in living cells can be described as strings of many thousands of smaller units called alleles. There are only four different kinds of alleles. In this simulation we reduce the number of different kinds of 'alleles' to 2 and the number of alleles in a 'chromosome' to 30. A simulated chromosome in our scheme can therefore be represented by a 30-digit binary number, for example:
001000010110111011100010111101The characteristics of an 'organism' is determined by the particular sequence of alleles in its chromosomes. In our simulation we parallel this concept by stating that the quality of any proposed binary number as a solution is determined by comparing it to an arbitrary ideal sequence which we are 'trying to find'. In this case for reasons of simplicity and clarity, we define the ideal as the largest possible 30-digit binary number, ie:
1111111111111111111111111111111As a first step the computer program generates a population of 10 chromosomes, each consisting of 30 randomly assigned 1's or 0's. It then converts each into its base 10 equivalent.
----------------------------------------------- POPULATION REPORT - INITIAL POPULATION Chromosome 111111111122222222223 123456789012345678901234567890 Value 1) 001000010110111011100010111101 140228800 2) 111100111101001010100100001101 1022667008 3) 100000110111011000100000100110 551389248 4) 010011100111001101010000111000 329045056 5) 010100001110010100110010001110 339299456 6) 100001111111111100011001111100 570410624 7) 011101101001001100000010010001 497336448 8) 111100011111011001101010011111 1014864512 9) 101101111111000011111111001100 771506112 10) 110111000011101101101001001011 923720256 -----------------------------------------------Next, an algorithm which we will not discuss at this time, assigns a relative fitness value to each proposed solution, and on the basis of these values selects the 10 chromosomes that will take part in the 'breeding' of the next generation.
------------------------------------------------------------- POPULATION REPORT - INITIAL POPULATION Chromosome 111111111122222222223 123456789012345678901234567890 Value Fitness Count 1) 001000010110111011100010111101 140228800 0.0000 0 2) 111100111101001010100100001101 1022667008 0.6142 4 3) 100000110111011000100000100110 551389248 0.0013 0 4) 010011100111001101010000111000 329045056 0.0000 0 5) 010100001110010100110010001110 339299456 0.0000 0 6) 100001111111111100011001111100 570410624 0.0018 0 7) 011101101001001100000010010001 497336448 0.0005 0 8) 111100011111011001101010011111 1014864512 0.5689 4 9) 101101111111000011111111001100 771506112 0.0367 0 10) 110111000011101101101001001011 923720256 0.2220 2 -------------------------------------------------------------The 'Fitness' value is a comparative index for how close the corresponding value is to the ideal. The 'Count' column indicates that 4 copies of chromosome #2, 4 copies of chromosome #8 and 2 copies of chromosome #10 have been selected (on the basis of the corresponding 'Fitness' values) for the breeding population. Note that these correspond to the largest binary numbers.
Here are the 'parents' of the next generation of solutions. The first member of the previous list has 'died'. The second member of the previous list is replicated 4 times. Numbers 3, 4, 5, 6, and 7 from the first list have also 'died' while the eighth is replicated four times. The tenth is replicated twice.
-------------------------------------------------------------- POPULATION REPORT - NEW POPULATION SELECTED Generation 1 Chromosome 111111111122222222223 123456789012345678901234567890 Value Fitness Count 1) 111100111101001010100100001101 1022667008 0.6142 4 2) 111100111101001010100100001101 1022667008 0.6142 4 3) 111100111101001010100100001101 1022667008 0.6142 4 4) 111100111101001010100100001101 1022667008 0.6142 4 5) 111100011111011001101010011111 1014864512 0.5689 4 6) 111100011111011001101010011111 1014864512 0.5689 4 7) 111100011111011001101010011111 1014864512 0.5689 4 8) 111100011111011001101010011111 1014864512 0.5689 4 9) 110111000011101101101001001011 923720256 0.2220 2 10) 110111000011101101101001001011 923720256 0.2220 2 --------------------------------------------------------------Next, the 10 breeders are paired at random and a random 'crossing site' is selected for each pair. In the following illustration #1 chromosome from the previous list has been paired with #9 and a crossing site of 14 has been assigned. The other pairs are similarly treated.
-------------------------------------------------------------- POPULATION REPORT - PAIRS AND CROSSING SITES RANDOMIZED Generation 1 Chromosome 111111111122222222223 123456789012345678901234567890 Value Fitness Count X.site 1) 111100111101001010100100001101 1022667008 0.6142 4 14 2) 110111000011101101101001001011 923720256 0.2220 2 14 3) 111100011111011001101010011111 1014864512 0.5689 4 15 4) 111100111101001010100100001101 1022667008 0.6142 4 15 5) 111100011111011001101010011111 1014864512 0.5689 4 9 6) 110111000011101101101001001011 923720256 0.2220 2 9 7) 111100011111011001101010011111 1014864512 0.5689 4 1 8) 111100111101001010100100001101 1022667008 0.6142 4 1 9) 111100011111011001101010011111 1014864512 0.5689 4 22 10) 111100111101001010100100001101 1022667008 0.6142 4 22 -------------------------------------------------------------------------Here we examine in detail what happens next with the first breeding pair. An 'x' has been inserted at the crossing site for clarification.
11111 x 1111122222222223 12345678901234 x 5678901234567890 Value Fitness Count X.site 1) 11110011110100 x 1010100100001101 1022667008 0.6142 4 14 2) 11011100001110 x 1101101001001011 923720256 0.2220 2 14The breeding process will create two individuals. The first offspring inherits alleles 1 to 14 from parent #1 and alleles 15 to 30 from parent #2. The second offspring inherits alleles 1 to 14 from parent #2 and alleles 15 to 30 from parent #1.The two offspring of the first pair of breeders will therefore have the pattern:
11111 x 1111122222222223 12345678901234 x 5678901234567890 1) 11110011110100 x 1101101001001011 2) 01011100001110 x 1010100100001101Here is the whole list:
-------------------------------------------------------------------------- CROSS OVERS AND RECALCULATE Generation 1 Chromosome 111111111122222222223 123456789012345678901234567890 Value Fitness Count Par1 Par2 Xsite 1) 111100111101001101101001001011 1022679616 0.6143 1 1 2 14 2) 010111000011101010100100001101 386836736 0.0000 1 1 2 14 3) 111100011111011001101010011111 1014864512 0.5689 1 3 4 15 4) 111100111101001010100100001101 1022667008 0.6142 1 3 4 15 5) 111100011011101101101001001011 1013897792 0.5635 1 5 6 9 6) 110111000111011001101010011111 924686976 0.2243 0 5 6 9 7) 111100110101001010101100001101 1020570368 0.6017 1 7 8 1 8) 111100011111011001101010011111 1014864512 0.5689 1 7 8 1 9) 111100011111011001101000001101 1014864384 0.5689 2 9 10 22 10) 111100111101001010100110011111 1022667136 0.6142 1 9 10 22 -------------------------------------------------------------------------- Generation 1 Total value: Mean value: Max. value: Min. value: 9.458599e+9 9.458599e+8 1.022680e+9 3.868367e+8 Total fitness: Mean fitness: Max. fitness: Min. fitness: 4.93916e+0 4.939156e-1 6.142892e-1 3.683443e-5 Number of cross overs: 4 Number of mutations: 3 --------------------------------------------------------------------------Not all of the remaining four pairs are similarly treated. Note for example that parents #3 and #4 from the original population did not participate in the cross over process, but are simply replicated in generation 1. Whether or not cross over occurs is randomly determined. The probability of cross over occurring somewhere is an arbitrary number in the upper range of 0 < p < 1.
In this listing the 'parents' of each of the new individuals is indicated, together with recalculated values for fitnesses which determine the counts of each to be used in the next breeding population. Note that the fitness coefficients for this first generation are generally higher than those of the original population. This is reflected in the more even distribution in the count column.
A crucial component of the evolutionary process is mutation. An arbitrary small percentage of the alleles have been 'mutated' by switching 1's to 0's or 0's to 1's. The last listing is accompanied by a statistical summary which indicates that 3 such mutations have taken place.
If the cycle is repeated many times there is an increase in the general quality of proposed solutions. In this instance this quality is reflected in a general increase in the mean of the values produced. The process is intended to mimic reproduction in nature and evolution through 'survival of the fittest'.
I think we have the idea now. Let's summarize to make sure.
We start with an initial population of 10 individuals whose random 30-digit binary numbers represent proposed solutions to a problem. In this case the problem is simply to find the maximum possible number.
We devise a method for picking candidates to 'breed' a new generation on the basis of how 'good' they are. Some individuals are used several times for breeding purposes. Many are not used at all. The selected solutions are mated at random and their digits swapped starting at random locations. The resulting population is subject to mutation, and the process starts over. The ultimate objective is to produce a 'super race' of perfect solutions.
We have over-simplified things a bit here; but it is intuitive that it is better to have large populations than to have smaller ones. We used populations of 10.
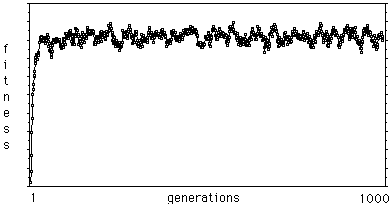
One would think that a population of 100 bred for 1000 generations should give pretty good results. Here is a graph of the mean values produced by each generation for such a run.
This Genetic Algorithm with these arbitrary parameters for cross over and mutation rate produces results which increase quickly in quality, reaching a maximum in around 50 generations. From then on there isn't any improvement.Research in the area of Genetic Algorithms has revealed a variety of techniques for improving the long range production of better solutions. A description of these are beyond the scope of this introductory paper.