Первоисточник - http://www.saltspring.com/brochmann/math/GA/GA-1.00.html
ГЕНЕТИЧЕСКИЙ АЛГОРИТМ
Гарольд Брочманн
Задачи, решаемые компьютерами могут быть характеризованы как детерминированные или недетерминированные. Детерминированные процедуры знакомы, и они применяются, когда есть только один, или ограниченное число правильных ответов, которые являются известной функцией доступных данных. Например, ответы на многие технические проблемы получены, описывая реальный объект стандартными формулами. Однако существуют не для решения таких задач, с которыми могут справиться калькуляторы. Это подразумевает написание компьютерных программ, которые описывают желательные функции, что является довольно прямолинейным занятием.
Для многих задач решения не описываются явно заданными функциями; часто алгоритм решения не может быть найден, или его, возможно, не существует. Рассмотрим задачу Коммивояжера, которая состоит в обнаружении самого эффективного маршрута коммивояжора (продавца), который хочет посетить некоторое число городов. Один подход состоит в том, чтобы вычислить длину всех возможных маршрутов. Трудность здесь состоит в том, что с увеличением числа посещаемых мест число возможных маршрутов становится настолько большим, что время, потраченное для компьютера, чтобы оценить их всех, становится огромным.
Техника для того, чтобы решать такие задачи, оценивает большое количество случайных решений, и затем отбирает лучшие из них. Такие предложенные решения отличаются от идеала так мало, что нет никакого смысла в дальнейшем рассмотрении вопроса. Это второй способ решения сложных задач.
Усовершенствование таких методов должно создать эффективные алгоритмы, которые производят лучшие решения на основе результатов, полученных, чтобы уменьшить вероятность ошибки.
Генетические Алгоритмы - компьютерные процедуры, которые используют принципы естественного выбора и естественной генетики, чтобы найти решение задачи. Цель этой статьи состоит в том, чтобы объяснить на примере общую структура таких алгоритмов.
Пример
- адаптация компьютерной программы, описанной в третьей главе книги
Genetic Algorithms in Search, Optimization &
Machine Learning by David E
Goldberg (Addison-Wesley, 1989).
Хромосомы, которые находятся в ячейках, могут быть описаны как последовательности многих тысяч меньших структур, названных аллелями. Есть только четыре различных вида аллелей. В этом моделировании мы уменьшаем число различных видов 'аллелей' к 2 и числа аллелей в 'хромосоме' к 30. Моделируемая хромосома в нашей схеме может поэтому быть представлена двоичным числом с 30 цифрами, например:
001000010110111011100010111101
Особенности «организма» определены специфической последовательностью аллелей в ее хромосомах. В нашем моделировании мы находим что-либо подобное этому понятию, заявляя, что качество любого предложенного двоичного числа как решение определено, сравнивая это с произвольной идеальной последовательностью, которую мы «пробуем найти». В этом случае по причинам простоты и ясности, мы определяем наилучшее решение как наибольшее двоичное число с 30 цифрами, то есть:
1111111111111111111111111111111
Как первый шаг компьютерная программа производит генерацию 10 хромосом, состоящих из 30 беспорядочно назначенных 1-ц или 0-ей. После чего преобразовывает их в десятичный эквивалент.
-----------------------------------------------
ОТЧЕТ О ПОПУЛЯЦИИ – ПЕРВАЯ ПОПУЛЯЦИЯ
111111111122222222223
123456789012345678901234567890 Значение
1) 001000010110111011100010111101 140228800
2) 111100111101001010100100001101 1022667008
3) 100000110111011000100000100110 551389248
4) 010011100111001101010000111000 329045056
5) 010100001110010100110010001110 339299456
6) 100001111111111100011001111100 570410624
7) 011101101001001100000010010001 497336448
8) 111100011111011001101010011111 1014864512
9) 101101111111000011111111001100 771506112
10) 110111000011101101101001001011 923720256
-----------------------------------------------
Затем, рассматриваемый алгоритм назначает относительную пригодность каждому решению, и на основе этих данных выбирает 10 хромосом, которые примут участие в создании следующего поколения.
-------------------------------------------------------------
ОТЧЕТ О ПОПУЛЯЦИИ – ПЕРВАЯ ПОПУЛЯЦИЯ
111111111122222222223
123456789012345678901234567890 Значение Фитнесс кол-во
1) 001000010110111011100010111101 140228800 0.0000 0
2) 111100111101001010100100001101 1022667008 0.6142 4
3) 100000110111011000100000100110 551389248 0.0013 0
4) 010011100111001101010000111000 329045056 0.0000 0
5) 010100001110010100110010001110 339299456 0.0000 0
6) 100001111111111100011001111100 570410624 0.0018 0
7) 011101101001001100000010010001 497336448 0.0005 0
8) 111100011111011001101010011111 1014864512 0.5689 4
9) 101101111111000011111111001100 771506112 0.0367 0
10) 110111000011101101101001001011 923720256 0.2220 2
-------------------------------------------------------------
Фитнесс функция - сравнительный индекс, отображающий насколько решение близко к идеалу. Колонка 'кол-во' указывает, что 4 копии хромосомы №2, 4 копии хромосомы №8 и 2 копии хромосомы №10 были отобраны (на основе фитнесс функции) для дальнейшего «размножения». Заметьте, что они соответствуют наибольшим двоичным числам.
Получены 'родители' следующего поколения решений. Первый член предыдущего списка 'умер'. Второй член предыдущего списка дублируется 4 раза. Номера 3, 4, 5, 6, и 7 от первого списка также 'умерли', в то время как восьмое дублируется четыре раза. Десятое дублируется дважды.
-------------------------------------------------------------- ОТЧЕТ О ПОПУЛЯЦИИ – СЛЕДУЮЩАЯ ПОПУЛЯЦИЯ
Поколение 1
111111111122222222223
123456789012345678901234567890 Значение Фитнесс кол-во
1) 111100111101001010100100001101 1022667008 0.6142 4
2) 111100111101001010100100001101 1022667008 0.6142 4
3) 111100111101001010100100001101 1022667008 0.6142 4
4) 111100111101001010100100001101 1022667008 0.6142 4
5) 111100011111011001101010011111 1014864512 0.5689 4
6) 111100011111011001101010011111 1014864512 0.5689 4
7) 111100011111011001101010011111 1014864512 0.5689 4
8) 111100011111011001101010011111 1014864512 0.5689 4
9) 110111000011101101101001001011 923720256 0.2220 2
10) 110111000011101101101001001011 923720256 0.2220 2
--------------------------------------------------------------
Затем, эти 10 решений скрещиваются наугад, и случайный 'участок пересечения' отобран для каждой пары. На следующей иллюстрации #1 хромосома от предыдущего списка была соединена с #9, причем участком пересечения была назначена 14 позиция.
--------------------------------------------------------------
ОТЧЕТ О ПОПУЛЯЦИИ - ПАРЫ И ПЕРЕСЕКШИЕСЯ СЛУЧАЙНЫЕ УЧАСТКИ
Поколение 1
111111111122222222223
123456789012345678901234567890 Значение Фитнесс кол-во Кс.сайт
1) 111100111101001010100100001101 1022667008 0.6142 4 14
2) 110111000011101101101001001011 923720256 0.2220 2 14
3) 111100011111011001101010011111 1014864512 0.5689 4 15
4) 111100111101001010100100001101 1022667008 0.6142 4 15
5) 111100011111011001101010011111 1014864512 0.5689 4 9
6) 110111000011101101101001001011 923720256 0.2220 2 9
7) 111100011111011001101010011111 1014864512 0.5689 4 1
8) 111100111101001010100100001101 1022667008 0.6142 4 1
9) 111100011111011001101010011111 1014864512 0.5689 4 22
10) 111100111101001010100100001101 1022667008 0.6142 4 22
-------------------------------------------------------------------------
Рассмотри подробно, что случается с первой парой размножения. 'x' был вставлен на пересекшемся участке для разъяснения.
11111 x 1111122222222223
12345678901234 x 5678901234567890 Значение Фитнесс кол-во 'x'
1) 11110011110100 x 1010100100001101 1022667008 0.6142 4 14
2) 11011100001110 x 1101101001001011 923720256 0.2220 2 14
Процесс размножения создаст двух потомков. Первое потомство наследует аллели 1 - 14 от родителя #1 и аллелей 15 - 30 от родителя #2. Второе потомство наследует аллели 1 - 14 от родителя #2 и аллелей 15 - 30 от родителя #1.Два потомка первой пары родителей будут иметь вид:
11111 x 1111122222222223
12345678901234 x 5678901234567890
1) 11110011110100 x 1101101001001011
2) 01011100001110 x 1010100100001101
Список:
--------------------------------------------------------------------------
КРОССИНГОВЕР
Поколение 1
111111111122222222223
123456789012345678901234567890 Значение Фитнесс кол-во Род1 Род2 'x'
1) 111100111101001101101001001011 1022679616 0.6143 1 1 2 14
2) 010111000011101010100100001101 386836736 0.0000 1 1 2 14
3) 111100011111011001101010011111 1014864512 0.5689 1 3 4 15
4) 111100111101001010100100001101 1022667008 0.6142 1 3 4 15
5) 111100011011101101101001001011 1013897792 0.5635 1 5 6 9
6) 110111000111011001101010011111 924686976 0.2243 0 5 6 9
7) 111100110101001010101100001101 1020570368 0.6017 1 7 8 1
8) 111100011111011001101010011111 1014864512 0.5689 1 7 8 1
9) 111100011111011001101000001101 1014864384 0.5689 2 9 10 22
10) 111100111101001010100110011111 1022667136 0.6142 1 9 10 22
--------------------------------------------------------------------------Поколение 1
Решение Итог: Сред.: макс.: мин.:
9.458599e+9 9.458599e+8 1.022680e+9 3.868367e+8
Фитнесс Итог: Сред.: макс.: мин.:
4.93916e+0 4.939156e-1 6.142892e-1 3.683443e-5
Кол-во кроссинговеров: 4
Количество мутаций: 3
--------------------------------------------------------------------------
Не все четыре пары подобно рассматриваются. Отметьте, например, что родители #3 и #4 от оригинальной популяции не участвовали в кроссинговере по процессу, однако просто копируются в поколении 1. Действительно ли кроссинговер происходит беспорядочно? Вероятность кроссинговера - произвольное число в диапазоне от 0 до 1.
В нашем случае, в полученные потомки объединяются с родителями для использования на следующем шаге. Заметьте, что коэффициенты фитнесс функции для этого поколения выше, чем таковые из оригинальной популяции. Это отражено в таблице.
Критический компонент эволюционного процесса - мутация. Произвольный маленький процент от аллелей 'видоизменяется', мутируя 1-у в 0-ль или 0-ль в 1-у. Последнее внесение в список сопровождается сообщением, которое указывает, что было проведено 3 таких мутации.
Если цикл повторить много раз, то качество предложенных решений увеличится. В этом случае это качество отражено в общем увеличении средних фитнесс функций. Процесс подражает воспроизводству в природе и «выживанию самого приспособленного».
Подведем итоги.
Мы начинаем с начальной популяции в 10 особей, чьи случайные двоичные числа с 30 цифрами представляют предложенные решения задачи. В этом случае задача состоит в том, чтобы просто найти максимальное возможное число.
Мы выбираем кандидатов, чтобы 'создать' новое поколение на основе того, насколько они хорошо они приспособлены. Некоторые особи используются несколько раз для «размножения». Многие не используются вообще. Отобранные решения скрещиваются наугад. Полученная популяция мутируется, а затем процесс повторяется. Окончательная цель состоит в дальнейшем улучшении наилучших решений.
Мы немного упростили, но можно догадаться, что большее число особей даст лучшие результаты. Мы использовали популяцию в 10 особей.
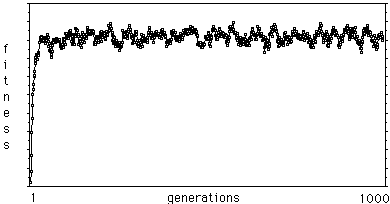
Очевидно, что популяция в 100 особей после 1000 поколений должна дать довольно хорошие результаты. На рисунке представлен граф средних фитнесс функций, произведенных каждым поколением для такого алгоритма.

Этот Генетический Алгоритм со случайными параметрами для кроссинговера и мутации производит решения, которые быстро приближаются к оптимальному (приблизительно в 50 поколениях).
Исследование в области Генетических Алгоритмов показало разнообразие методов усовершенствования метода. Описание их - вне возможностей данной статьи.