Н.Б. Паклин, М.А. Сенилов, В.А. Тененев

ГОУ ВПО "Ижевский государственный технический университет", г. Ижевск

ИНТЕЛЛЕКТУАЛЬНЫЕ МОДЕЛИ НА ОСНОВЕ ГИБРИДНОГО ГЕНЕТИЧЕСКОГО АЛГОРИТМА С ГРАДИЕНТНЫМ ОБУЧЕНИЕМ ЛИДЕРА

Данный доклад в сентябре 2004 г. был опубликован в научно-теоретическом журнале "Искусственный интеллект" и апробирован на V Международной конференции "Искусственный интеллект-2004. Интеллектуальные и многопроцессорные системы" (20-25 сентября 2004 года, Крым, п. Кацивели, ссылка на печатный источник: Паклин Н.Б., Сенилов М.А., Тененев В.А. Интеллектуальные модели на основе гибридного генетического алгоритма с градиентным обучением лидера // Искусственный интеллект. - Донецк: Наука i освiта. - 2004. - № 4. - С. 159-168.

Доклад был удостоен премии как лучший секционный доклад молодого ученого и рекомендован оргкомитетом конференции к публикации в ведущих центральных научных журналах России.

В работе для решения оптимизационных задач предлагается гибридный алгоритм, объединяющий стандартные генетические алгоритмы и градиентные методы. Особенность алгоритма в том, что работа градиентных и генетических методов ведется параллельно. Это позволяет находить глобальный оптимум с высокой точностью. Метод протестирован на овражных, многоэкстремальных функциях большой размерности без задания начального приближения. Показана эффективная работа алгоритма в процедуре обучения многослойного персептрона.

Введение

Практически все методы обучения интеллектуальных моделей используют какой-либо алгоритм глобальной оптимизации, минимизирующий функцию ошибки модели. Специфика оптимизируемых функций связана с большим размером пространства поиска и их многоэкстремальностью. Поэтому от применяемого алгоритма оптимизации в конечном итоге зависит качество полученной интеллектуальной модели.
Для решения задач глобальной оптимизации мноэкстремальных функций большой размерности разработано множество подходов. Одним из них является применение генетических алгоритмов как методов направленного случайного поиска. Сильной стороной генетических алгоритмов является их способность решать многоэкстремальные задачи без наложения условий на вид оптимизируемой функции и задания начального приближения. Однако достижения глобального экстремума генетические алгоритмы не гарантируют. Считается, что отыскивается сравнительно "хорошее" решение. Кроме того, с увеличением размерности оптимизируемой функции точность находимого оптимума снижается.

1. Генетический алгоритм с градиентным обучением лидера

Стандартный генетический алгоритм [1] не позволяет решить все проблемы, связанные с оптимизаций функций многих переменных. С увеличением раз-мерности вектора переменных сильно увеличивается размер области поиска. Рассмотрим пример поиска минимума тестовой функции Розенброка. Двумерная функция имеет вид:

(1)

Оптимальные значения переменных при равны . N-мерная функция Розенброка, взятая как в работе [2] при N=24, запишется в виде

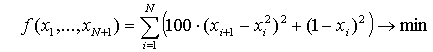. (2)

Оптимальные значения переменных при f(X)=0 также равны . Для минимизации функции (2) в области применялся стандартный генетический алгоритм с бинарным кодированием. На рис. 1 показаны зависимости от числа итераций k значений функции f(X) при N=24 (линия 1) и N=1 ( линия 4), а также максимальные отклонения от точного решения (линии 2 и 5) и среднеквадратичные отклонения (линии 3 и 6), соответственно для N=24 и N=1. Для функции с N=1 минимальное значение достигает приемлемого уровня при отклонении от точного решения до . В случае же N=24 сходимость процесса гораздо хуже. Значения функции не опускаются ниже 30 и максимальное отклонение от точного решения устанавливается на уровне 1 (т.е. для некоторых решение находится далеко от оптимального). Это связано с тем, что функция Розенброка имеет выраженный овражный характер.

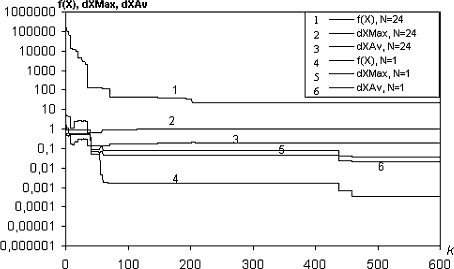
Рисунок 1 - Минимизация функции Розенброка стандартным
генетическим алгоритмом

При небольшой размерности задачи N=1 генетический алгоритм находит дно оврага и выходит на приемлемое решение. При увеличении размерности до N=24 вероятность попадания в нужный овраг существенно уменьшается и итерационный процесс "замораживается". Градиентные методы при случайном выборе начального приближения в области также застревают в областях локальных минимумов. Данные результаты заставляют искать пути повышения эффективности генетических алгоритмов.

Развитие генетических алгоритмов с целью увеличения скорости сходимости ведется по пути создания новых разновидностей операторов отбора, скрещивания и мутации. Разрабатываются методы распараллеливания генетических ал-горитмов [3]. Интенсивно развиваются динамические генетические алгоритмы, в которых в процессе итераций изменяются их параметры [4]. Как правило, введенные усовершенствования показывают улучшение эффективности на тестовых за-дачах небольшой размерности. При увеличении N проблема нахождения глобаль-ного экстремума овражных функций остается актуальной.
Еще одним направлением улучшения работы оптимизационных методов является применение гибридных алгоритмов, объединяющих свойства градиентных и эволюционных алгоритмов [5]. Обычно находят начальное приближение, локализованное в области экстремума, с помощью генетического алгоритма, а затем уточняют положение экстремума градиентным методом, т.е. ведется последо-вательная работа алгоритмов. В этом случае также ускоряется сходимость и по-вышается точность, но экстремум не обязательно будет глобальным.

В нашей работе исследуется гибридный алгоритм, основанный на параллельной работе генетических операторов и какого-либо градиентного метода. В популяции, созданной генетическим алгоритмом, выбирается лучшая особь - ли-дер. Этот лидер обучается отдельно по градиентному методу. Если его качественный показатель при этом лучше, чем у всех остальных особей в популяции, то он вводится в популяцию и участвует в воспроизводстве потомков. Если же появля-ется особь в популяции, полученная в результате эволюции, с лучшим показателем, то лидером становится она. Исследование предлагаемого гибридного алгоритма проводилось на основе двух видов генетических алгоритмов (в бинарных и вещественных кодах) и трех типов градиентных методов (метод наискорейшего спуска, метод сопряженных градиентов, квазиньютоновский метод или метод переменной метрики).
Рассмотрим задачу оптимизации многомерной функции:

(3)

и некоторые оптимизационные методы.

1. Стандартный генетический алгоритм с бинарным кодированием (BGA).
Перед началом процесса при k=0 формируется популяция, состоящая из m особей. Особь или хромосома представляется в виде , где - вектор аргументов функции; - преобразование, осуществляющее переход от вектора X (фенотипа) к кодированному представлению (генотипу); - битовая строка длиной ; - разрядность представления переменной xi.

Преобразование

- векторы целочисленного представления, двоичного представления и представления в коде Грея.

Обратное преобразование

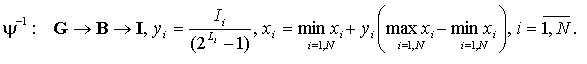
Проводится эволюция популяции на итерации k=k+1 с использованием операторов отбора, скрещивания и мутации [1].

2. Генетический алгоритм в вещественных кодах (RGA).
Многочисленные исследования результатов разработки генетических алгоритмов вещественного кодирования проведены в работе [2]. Основная идея RGA заключается в том, чтобы напрямую представлять гены в виде вещественных чисел, т.е. генотип объекта становится идентичным его фенотипу. Вектор хромосомы представляет собой вектор вещественных чисел , и точность найденного решения будет определяться не количеством разрядов для кодирования битовой строки, а будет ограничена возможностями ЭВМ, на которой реализуется вещественный ГА. Последовательность операций в таком алгоритме такая же, как и в стандартном генетическом алгоритме бинарного кодирования. Отличие заключается в виде генетических операторов. Преобразование здесь сильно упрощается (осуществляется лишь приведение аргументов к безразмерному виду):

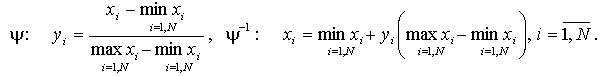
Оператор скрещивания имеет вид (один из рекомендованных в работе [2]):

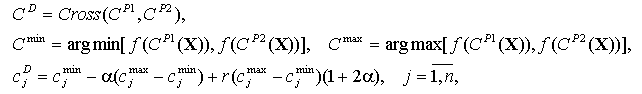
где - параметр кроссовера; - случайное число.

Оператор мутации задает случайным образом значения .

В результате проведенных экспериментов генетические алгоритмы бинарного и вещественного кодирования показали примерно одинаковую эффективность. С увеличением размерности задачи глобальный экстремум функции Розенброка достигается не всегда. Для генетический алгоритм вещественного кодирования начинает проигрывать алгоритму бинарного кодирования. Бинарный алгоритм уверенно находит глобальный экстремум до . При больших значениях оптимальное решение находится не всегда. Алгоритм вещественного кодирования при N=10 застревает в локальных экстремумах.
Гибридный алгоритм [6].

1. k=0. Формируется популяция, состоящая из m особей по BGA или RGA методу. Первый номер принимает особь с лучшим показателем (минимальным значением функции (3)). С помощью преобразования получаем вектор и .
2. k=k+1. С помощью одного из градиентных алгоритмов вычисляется следующее приближение вектора . Генетическим алгоритмом BGA или RGA создается следующая популяция и находится лучшая особь, определяющая очередной вектор .
3. Если , то .
4. Если , то .
5. Если выполняется условие остановки, то конец, иначе на пункт 2.


2. Тестирование гибридного алгоритма

Анализ градиентных методов показал, что наиболее предпочтительным для использования в гибридном алгоритме является метод переменной метрики (VM), имеющий более высокую скорость сходимости.
На рис. 2 показаны результаты минимизации функции Розенброка при N=2 гибридным алгоритмом. Зависимости (1)-(3) соответствуют гибридному алгоритму: бинарный генетический алгоритм + метод переменной метрики (BGAVM). Зависимости (4)-(6) - вещественный генетический алгоритм + метод переменной метрики (RGAVM). По сравнению с рис.1 видно, что функция за несколько итераций уменьшается на восемь порядков до величины 10e-6. Количество необходи-мых итераций меньше в сотни раз, по сравнению со стандартным генетическим алгоритмом.

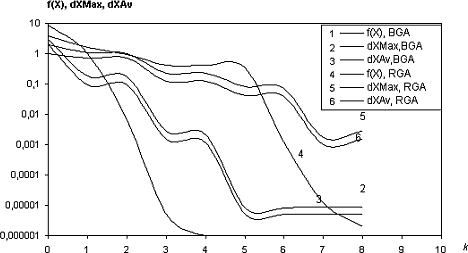
Рисунок 2 - Минимизация функции Розенброка гибридным
генетическим алгоритмом, N=1




Рисунок 3 - Минимизация функции Розенброка гибридным
генетическим алгоритмом BGAVM, N=200

Далее гибридный алгоритм тестировался на функции Розенброка большей размерности N=200. Зависимости функции и ошибок аргументов представлены на рис. 3 от величины t в условных единицах, соответствующих 1 секунде работы процессора. Количество итераций при этом равно 207.
Анализ работы гибридного алгоритма показал, что основная часть работы выполняется в режиме "если , то " - лидер обучается по методу переменной метрики и улучшает популяцию в целом. Смена лидера происходит не так часто - примерно на 1%-5% итераций. Алгоритм RGAVM также показал хорошую производительность. Число итераций для него больше в 2-3 раза, но время, затрачиваемое на одну итерацию, в 2,5 раза меньше. Поэтому по затратам вычислительного времени оба алгоритма дают близкие результаты.

Рисунок 4 - Траектория проекции движения представляющей точки,
алгоритм BGAVM, N=200

На рис. 4 показана проекция траектории движения представляющей точки к оптимуму. Проекция сделана на две координаты с максимальными отклонениями от точного решения. Худшие решения находятся далеко от оврага. Попадание в овраг осуществляется по генетическому алгоритму, а затем достаточно быстро определяются оптимальные значения этих переменных и положение глобального экстремума.

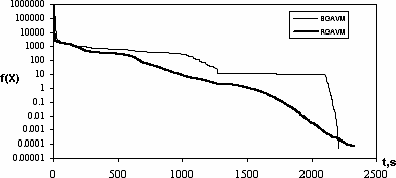
Рисунок 5 - Минимизация функции Розенброка гибридными генетическими алгоритмами BGAVM и RGAVM, N=2000

На следующем этапе тестирования гибридного алгоритма минимизирова-лась функция Розенброка при N=2000. Задача поиска глобального экстремума функции большой размерности также успешно решена обоими методами BGAVM и RGAVM примерно за одинаковое время (рис. 5). Для метода BGAVM выполнено 620 итераций, для метода RGAVM - 1360. Следует отметить, что ни метод BGA, ни RGA, ни VM не позволили получить значения минимизируемой функции меньше 10000.

Кроме функции Розенброка рассматривались другие функции, обычно применяемые при тестировании [2]:

функция Растригина
функция de Jong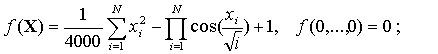
функция

Результаты оптимизации функций приведены в табл. 1.

Таблица 1 - Показатели сходимости на тестовых функциях, N=24

Рассмотренные функции удовлетворительно минимизируются стандартным генетическим алгоритмом. Хотя алгоритм BGAVM проводит оптимизацию рассмотренных функций значительно быстрее стандартных алгоритмов, эти функции менее показательны по сравнению с функцией Розенброка. На многомерной функции Розенброка глобальный оптимум достигается только методами BGAVM и RGAVM. В работе [6] показана эффективная работа гибридного алгоритма для решения широкого круга задач большой размерности: условной опти-мизации, решении систем нелинейных алгебраических уравнений и вариационных задач.

3. Гибридный алгоритм для обучения интеллектуальных моделей

Рассмотрим возможность применения предложенного гибридного генетического алгоритма с градиентным обучением лидера в процедурах обучения интеллектуальных моделей.

Рассмотрим возможность применения предложенного гибридного генетического алгоритма с градиентным обучением лидера в процедурах обучения интеллектуальных моделей.
В случае многослойного персептрона [7] настройка весовых коэффициентов нейронной сети производится из условия минимума среднеквадратичной ошибки прогнозирования по всей обучающей выборке . В этом случае целевая функция принимает вид:

Сравним результаты обучения такой нейронной сети на примере двумерной тестовой функции Розенброка (1). Функция определена в области . Значения функции вычислены в узлах равномерной сетки , всего 441. Рассмотрим три метода обучения: простейший градиентный метод Back Propagation (BP); метод бинарного кодирования BGA; гибридный алгоритм BGAVM.

Показателями качества обучения служат два параметра: среднеквадратичное отклонение и коэффициент корреляции r между . Полученные лучшие показатели обучения для всех трех методов приведены в табл. 2.

Таблица 2.

Метод	BP	BGA	BGAVM
	0.056	0.052	0.012
r	0.912	0.921	0.997

Сравнение рассчитанных значений y с фактическими d на тестовой выборке, составляющей 50% от всех точек, приведено на рис. 6, 7. Значения y и d нормированы в диапазон [0;1].

Рисунок 6 - Сравнение рассчитанных и фактических значений на тестовой
выборке: слева - простейший градиентный метод, справа - метод BGA

Из рис. 6 следует, что методы BP и BGA плохо воспроизводят функцию в области оврага. Метод BGAVM (рис. 7) проводит обучение значительно лучше во всем диапазоне данных.

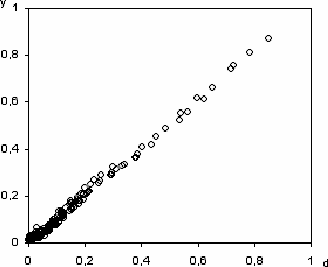
Рисунок 7 - Сравнение рассчитанных и фактических значений на тестовой
выборке, метод BGAVM

Укажем основные направления применения гибридного ГА в обучении других интеллектуальных моделей. В радиальной нейронной сети [7] можно предложить минимизацию целевой функции

.

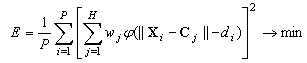алгоритмом BGAVM или RGAVM относительно неизвестных: параметров радиальных функций и весовых коэффициентов . При этом возможны два варианта:

1. Расчет всех неизвестных коэффициентов на каждой итерации;
2. Двухэтапный расчет, в котором итерации подразделяются на внутренние и внешние. На внутренних итерациях оптимизационным методом BGAVM или RGAVM находятся параметры радиальных функций . На внешней итерации рассчитываются весовые коэффициенты с помощью псевдоинверсии матрицы радиальных функций.

В нечеткой нейронной сети TSK [7] предлагаемый гибридный генетиче-ский алгоритм целесообразно использовать на этапе подбора параметров обоб-щенных гауссовских функций принадлежности. В этом случае градиент целевой функции будет рассчитываться по конечно-разностной формуле.

Заключение

1. Применение гибридной схемы для генетического алгоритма, основанной на дополнительном обучении квазиньютоновским методом лучшего представите-ля популяции, дало эффект - "сумма больше составляющих частей". В результате стало допустимым решение задач, невозможное при использовании каждого метода в отдельности.
2. Результаты тестовых исследований показали возможность использова-ния гибридного генетического алгоритма с градиентным обучением лидера для решения широкого круга задач большой размерности: условная оптимизация, на-хождение корней систем нелинейных уравнений, оптимизация динамических систем, обучение искусственных нейронных сетей и гибридных интеллектуальных систем.

(с) 2004 Паклин Н.Б., Тененев В.А., Сенилов М.А.

Обсудить статью на форуме

ЛИТЕРАТУРА

1. Курейчик В.М. Генетические алгоритмы // Перспективные информационные технологии и интеллектуальные системы. - 2000. - № 1.- С.18-22.
2. Herrera F., Lozano M., Verdegay J.L. Tackling real-coded genetic algorithms: operators and tools for the behaviour analysis // Artificial Intelligence Review, Vol. 12, No. 4, 1998. - PP. 265-319.
3. Родзин С.И. Формы реализации и границы применения эволюционных алгоритмов // Перспективные информационные технологии и интеллектуальные системы. - 2002. № 1. с.36-41.
4. Курейчик В.М., Зинченко Л.А., Хабарова И.В. Алгоритмы эволюционного моделирования с динамическими параметрами // Информационные технологии. - 2001. - № 6. - С.10-15.
5. Комарцова Л.Г. Двухэтапный алгоритм обучения нейронной сети на основе генетического поиска // Нейрокомпьютеры: разработка и применение. - М.: Радиотехника. - 2001. - № 1. - С. 3-9.
6. Тененёв В.А., Паклин Н.Б. Гибридный генетический алгоритм с дополнительным обучением лидера // Интеллектуальные системы в производстве. - 2003. - № 2. - Ижевск: Изд-во ИжГТУ, 2003. - С. 181-206.
7. Осовский С. Нейронные сети для обработки информации. - М.: Финансы и статистика, 2002. - 344 с.


In the paper for optimization problems solving the hybrid algorithm combining standard genetic algorithms and gradient methods is offered. Feature of algorithm is that operation of gradient and genetic methods is realized in parallel mode. It allows finding a global optimum with high accuracy. The method is tested on ravine multiextremal functions of the high dimensionality without the initial approximation. Effective work of the hybrid algorithm in procedure of learning multilayer perceptron is shown.

О других применениях гибридного ГА подробно написано в следующих статьях:

Тененев В.А., Паклин Н.Б. Гибридный генетический алгоритм с дополнительным обучением лидера // Интеллектуальные системы в производстве. - 2003. - № 2. - Ижевск: Изд-во ИжГТУ, 2003. - С. 181-206. (в формате PDF)

Тененев В.А., Паклин Н.Б. Оптимальное управление распределением средств товаропроизводителей // Системный анализ в проектировании и управлении: Труды VIII Междунар. науч.-практ. конф. - Ч. 1. - СПб.: Изд-во СПбГПУ, 2004. - С. 235-239. (в формате PDF)