Вернуться в библиотеку
Первоисточник - http://paklin.newmail.ru/mater/rcga.html

ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ С ВЕЩЕСТВЕННЫМ КОДИРОВАНИЕМ

(REAL-CODED GENETIC ALGORITMS)

В материале рассказывается о генетических алгоритмах, в которых хромосома представляется вектором вещественных чисел. Такой вид ГА получил название генетическиго алгоритма с вещественным кодированием (Real-Coded GA). В отличие от классического ГА, в real-coded алгоритме нет необходимости в операциях кодирования/декодирования. Описаны специальные операторы кроссовера и мутации для данного вида алгоритма. Приведены результаты экспериментов. Доступен для скачивания VCL компонент, реализующий класс TRealCodedGeneticAlgorithm и тестовая программа.

Вся информация взята из иностранных источников, поскольку в русскоязычной литературе и в Рунете материалов, посвященных Real-Coded GAs, не наблюдается. Обширные сведения из теории ГА с вещественным кодированием можно почерпнуть из [Herrera, 1998].

Идея использовать в виде хромосомы вектор вещественных значений появилась у исследователей в области ГА при решении задач непрерывной оптимизации.Двоичное представление хромосом влечет за собой определенные трудности при выполнении поиска в непрерывных пространствах, которые связаны с большой размерностью пространства поиска.

Как известно, для кодирования признака, принимающего действительные значения в некотором диапазоне, в битовую строку, используется специальный прием. Интервал допустимых значений признака xi разбивают на участки с требуемой точностью. Для преобразования целочисленного значения гена из множества в вещественное число из интервала пользуются формулой:

,

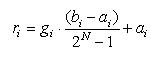где N - количество разрядов для кодирования битовой строки. Чаще всего используются значения N = 8; 16; 32.

При увеличении N пространство поиска расширяется и становится огромным. В иностранных источниках по RGA часто приводится такой пример. Пусть для 100 переменных, изменяющихся в интервале [-500; 500], требуется найти минимум с точностью до шестого знака после запятой. В этом случае при использовании ГА с двоичным кодированием длина строки составит 3000 элементов, а пространство поиска - около 10 в степени 1000.

Для решения таких задач в непрерывных пространствах возник новый тип ГА - генетический алгоритм с вещественным кодированием (англ.: Real-coded Genetic Algorithm, RGA) [Herrera, 1998], [Michalewich, 1995], [Wright, 1991]. Основная идея RGA заключается в том, чтобы напрямую представлять гены в виде вещественных чисел, т.е. генотип объекта становится идентичным его фенотипу. Вектор хромосомы состоит из вектора вещественных чисел, и точность найденного решения будет определяться не количеством разрядов для кодирования битовой строки, а будет ограничена возможностями ЭВМ, на которой реализуется вещественный ГА.

Применение вещественного кодирования может повысить точность найденных решений и повысить скорость нахождения глобального минимума или максимума. Скорость повышается из-за отсутствия процессов кодирования и декодирования хромосом на каждом шаге алгоритма.
Для RGA стандартные операторы скрещивания и мутации не подходят, т.к. алгоритм работает только с вещественными числами. По этой причине были разработаны и исследованы специальные операторы. Наиболее полный их обзор приведен в [Herrera, 1998].

Рассмотрим их подробно. Пусть и - две хромосомы, выбранные оператором селекции для проведения кроссовера.

1. Плоский кроссовер (англ.: flat crossover). Создается потомок , где - случайное число их интервала .

2. Арифметический кроссовер (англ.: arithmetical crossover). Создаются два потомка и :

, - константа.

3. кроссовер. Генерируется один потомок , где - случайное число из интервала ,

4. Линейный кроссовер (англ.: linear crossover). Создаются три потомка, рассчитываемые по формулам:

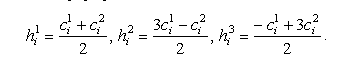
На этапе селекции в линейном кроссовере выбираются две особи с наи-большими приспособленностями.

В качестве оператора мутации наибольшее распространение получили: случайная и неравномерная мутация Михалевича.
При случайной мутации ген , подлежащий изменению, принимает случайное значение из интервала своего изменения .
В неравномерной мутации значение гена после оператора мутации рассчитывается по формуле:


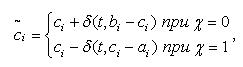
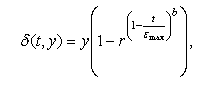
где - целое случайное число, принимающее значение 0 или 1; - случайное вещественное число; - максимальное количество эпох алгоритма; b - параметр, задаваемый исследователем.

В работе [Herrera, 1998] проведен ряд экспериментов на тестовых функциях с использованием разных типов операторов скрещивания и мутации для ГА с вещественным кодированием (RGA). Например, классической тестовой функцией является N-мерная функция Розенброка, имеющая вид

Оптимальные значения переменных при f(X)=0 равны , . Данная функция имеет выраженный овражный характер.

Кроме того, полученные результаты сравнивались с результатами работы ГА с двоичным (бинарным) кодированием BGA. В этой работе сделан вывод о том, что в большинстве случаев генетический алгоритм с вещественным кодированием справляется с задачей отыскания оптимума лучше и быстрее, чем с двоичным кодированием. Самым эффективным оператором скрещивания признан кроссовер с . Особенность данного оператора в том, что при скрещивании генов значения потомка могут лежать в некоторой области, выходящей за границы значений этих генов на величину , т.е. В других кроссоверах, например, в плоском или арифметическом,

Наши исследования не подтвердили превосходство RGA перед BGA. Эксперимент заключался в следующем: был взят VCL-компонент для Delphi TGeneticAlgorithm, реализующий стандартный бинарный алгоритм Холланда с турнирным методом отбора. Данный компонент распространяется свободно и доступен для скачивания на сайте компании BaseGroup. Далее, этот компонент был модернизирован в RGA-алгоритм TRealCodedGeneticAlgorithm. В нем отсутствуют операции кодирования/декодирования, реализован кроссовер и два вида мутации: равномерная и Михалевича. Остальные строки кода оставлены практически без изменений.

На тестовой многоэкстремальной функции Розенброка с увеличением N генетический алгоритм вещественного кодирования RGA начинает проигрывать алгоритму бинарного кодирования BGA. Бинарный алгоритм уверенно находит глобальный экстремум до N<=10. Алгоритм вещественного кодирования при N = 10 застревает в локальных экстремумах. Хотя, надо отдать должное алгоритмы RGA - его вычислительная сложность меньше - время затрачиваемое на одну итерацию в 2.5 раза меньше по спавнению с BGA из-за отсутствия процедур кодирования/декодирования

Поэтому нами был сделан вывод о том, что стандартный генетический алгоритм вещественного кодирования, более простой в реализации, существенно уступает стандартному алгоритму бинарного кодирования. Хотя в работе [Herrera, 1998] на многочисленных экспериментах доказывается обратное. Может быть, у Вас будут такие же результаты. Попробуйте!

    (с) 2004 Паклин Н.

ИСПОЛЬЗОВАННЫЕ ИСТОЧНИКИ
(c) 2003-2004 by Паклин Н.Б. / При использовании материалов ссылка обязательна