Оригинал материала находится здесь: http://cache.rcom.ru/~dap/nneng/nnlinks/nbdoc/ideal.htm
Многие задачи: распознавания образов
(зрительных, речевых и т.д.), выполнения функциональных преобразований при
обработке сигналов, управления, прогнозирования, идентификации сложных систем и
т.д. -сводятся к следующей математической постановке. Необходимо построить
отображение 
такое, чтобы на каждый возможный входной сигнал X формировался правильный
выходной сигнал Y. Отображение задается конечным набором пар
(<вход>, <известный выход>). Число таких пар (обучающих примеров)
существенно меньше общего числа возможных сочетаний значений входных и выходных
сигналов. Совокупность всех обучающих примеров носит название обучающей
выборки.
В задачах распознавания образов X - некоторое представление образа (изображение, вектор чисел и т.д.), Y - номер класса, к которому принадлежит входной образ.
В задачах управления X - набор контролируемых параметров управляемого объекта, Y - код, определяющий управляющее воздействие, соответствующее текущим значениям контролируемых параметров.
В задачах прогнозирования в качестве входных сигналов используются временные ряды, представляющие значения контролируемых переменных на некотором интервале времени. Выходной сигнал - множество переменных, которое является подмножеством переменных входного сигнала.
При идентификации X и Y представляют входные и выходные сигналы системы соответственно.
Вообще говоря, большая часть прикладных задач может быть сведена к реализации сложного многомерного функционального преобразования.
В результате построения отображения 
необходимо добиться того, чтобы:
Второе требование в значительной степени усложняет задачу формирования обучающей выборки. Эта задача в общем виде в настоящее время не решена. Однако во всех известных случаях было найдено частное решение. Дальнейшие рассуждения предполагают, что обучающая выборка уже сформирована.
Отображение 
в общем случае является многомерным, то есть X и Y - вектора с
размерностью больше единицы. Построить отображение - это значит представить его
с помощью традиционных математических операций, которые, в частности, легко
могут быть реализованы на персональном компьютере. Примеры таких операций:
сложение, умножение, деление, SIN, COS и т.д. Эти операции имеют не более двух
переменных (аргументов).
Проблема представление функций многих переменных в виде суперпозиции функций меньшего числа переменных восходит еще к так называемой 13-й проблеме Гильберта. Этот математик предполагал, что представить функцию многих переменных в виде суперпозиции функций меньшего числа переменных невозможно.
В результате многолетней научной полемики между А.Н. Колмогоровым и В.И. Арнольдом был получен целый ряд важных теоретических результатов, опровергающих тезис Гильберта:
Последний, наиболее сильный результат в 1987 году был переложен Хехт-Нильсеном в термины теории нейронных сетей [4].
Теорема Хехт-Нильсена доказывает
представимость функции многих переменных достаточно общего вида 
с помощью двухслойной нейронной сети с прямыми полными связями (рис. 1) с
N компонентами входного сигнала, 2N+1 компонентами первого
("скрытого" слоя) с заранее известными ограниченными функциями активации
(например, сигмоидальными) и M компонентами второго слоя с неизвестными
функциями активации. Теорема, таким образом, в неконструктивной форме доказывает
решаемость задачи представления функции достаточно произвольного вида на НС и
указывает для каждой задачи минимальные значения числа нейронов сети,
необходимых для решения.
Рис. 1. Многослойная нейронная сеть.
Следствие 1. Из теоремы в формулировке Хехт-Нильсена следует представимость любой многомерной функции нескольких переменных с помощью нейронной сети фиксированной размерности. Неизвестными остаются следующие характеристики функций активации нейронов:
Про функции активации нейронов второго слоя из теоремы Хехт-Нильсена известно только то, что они - нелинейные функции общего вида. В одной из работ, продолжающих развитие теории, связанной с рассматриваемой теоремой, доказывается, что функции нейронов второго слоя должны быть монотонно возрастающими. Это утверждение в некоторой степени сужает класс функций, которые могут потребоваться при реализации отображения с помощью двухслойной нейронной сети.
На практике требования теоремы Хехт-Нильсена к функциям активации удовлетворяют следующим образом. В нейронных сетях как для первого, так и для второго слоя используют сигмоидальные передаточные функции с настраиваемыми параметрами. То есть, в процессе обучения индивидуально для каждого нейрона настраиваются следующие параметры функций активации:
Следствие 2. В монографии [6]
показано, что для любого множества пар (Xk, yk)
(где yk - скаляр) существует двухслойная однородная (с
одинаковыми функциями активации) нейронная сеть первого порядка с
последовательными связями и с конечным числом нейронов, которая выполняет
отображение 
,
выдавая на каждый входной сигнал Xk правильный выходной сигнал
yk. Нейроны в такой двухслойной нейронной сети должны иметь
сигмоидальные передаточные функции. К сожалению, эта теорема не конструктивна. В
ней не заложена методика определения числа нейронов в сети для некоторой
конкретной обучающей выборки.
Для многих задач единичной размерности
выходного сигнала не достаточно. Необходимо иметь возможность строить с помощью
нейронных сетей функции 
,
где Y имеет произвольную размерность. Следующее утверждение является
теоретической основой для построения таких функций на базе однородных нейронных
сетей.
Утверждение. Для любого множества пар входных-выходных векторов произвольной размерности {(Xk, Yk), k=1...K} существует двухслойная однородная нейронная сеть с последовательными связями, с сигмоидальными передаточными функциями и с конечным числом нейронов, которая для каждого входного вектора Xk формирует соответствующий ему выходной вектор Yk.
Доказательство. Пусть выходные векторы Yk имеют размерность N, то есть Yk=(yk1, yk2,... yki,... ykN). В соответствии со следствием из теоремы Колмогорова-Арнольда для любого множества пар {(Xk, yki), k=1...K} существует двухслойная однородная нейронная сеть с последовательными связями и с сигмоидальными передаточными функциями, которая для каждого входного вектора Xk формирует соответствующий ему выходной скаляр yki. Такая нейронная сеть существует для каждого номера элемента выходного вектора i=1..N. Во втором слое эти сети содержат по одному нейрону. Пусть в первом слое сети, соответствующей элементу выходного сигнала с номером i содержится Mi нейронов.
Построим двухслойную однородную нейронную сеть с последовательными связями и с сигмоидальными передаточными функциями, содержащую в первом слое (M1+M2+...Mi+...MN) нейронов. Значения весов и смещений нейронов первого слоя равны соответствующим значениям нейронов сетей, построенных для пар (Xk, yki). Связи в этой сети между нейронами первого и второго слоев определим следующим образом. Значения синаптических весов первых M1 связей и значение смещения первого нейрона второго слоя совпадают с соответствующими значениями сети, построенной для пар (Xk, yk1). Остальные синаптические веса первого нейрона - нулевые. Значения синаптических весов связей с номерами (M1+1)...M2 и значение смещения второго нейрона второго слоя совпадают с соответствующими значениями сети, построенной для пар (Xk, yk2). Значения остальных синаптических весов второго нейрона равны нулю. Аналогично строятся синаптические веса и смещения других нейронов второго слоя.
В результате такого построения получаем двухслойную однородную нейронную сеть с последовательными связями, с сигмоидальными передаточными функциями и с конечным числом нейронов, которая для каждого входного вектора Xk формирует соответствующий ему выходной вектор Yk. Это доказывает утверждение.
Таким образом, для представления многомерных функций многих переменных может быть использована двухслойная однородная нейронная сеть с сигмоидальными передаточными функциями.
Для оценки числа нейронов с скрытых слоях однородных нейронных сетей можно воспользоваться формулой для оценки необходимого числа синаптических весов Nw в многослойной сети с сигмоидальными передаточными функциями [7]:
,
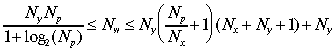где Ny - размерность выходного сигнала, Np - число элементов обучающей выборки, Nx - размерность входного сигнала.
Оценив необходимое число весов, можно рассчитать число нейронов в срытых слоях. Например, число нейронов в двухслойной сети составит:
Аналогично можно рассчитать число нейронов в сетях с большим числом слоев.
Иногда целесообразно использовать сети с большим числом слоев. Такие многослойные нейронные сети могут иметь меньшие размерности матриц синаптических весов нейронов одного слоя, чем двухслойные сети, реализующие то же самое отображение. К сожалению, строгая методика построения таких сетей пока отсутствует.
Аналогичная ситуация и с многослойными сетями, в которых помимо последовательных связей используются и прямые (то есть связи от слоя с номером m к слою с номером m+s, где s>1). Нет строгой теории, которая показывала бы возможность и целесообразность построения таких сетей.
Наибольшие проблемы возникают при использовании так называемых сетей циклического функционирования. К этой группе нейросетевых моделей относятся многослойные сети с обратными связями (от слоя с номером m к слою с номером m+s, где s<0), а также полносвязные сети. Для успешного функционирования этих моделей необходимо соблюдение условий динамической устойчивости. В противном случае при функционировании сеть может не сойтись к правильному решению, либо достигнув на некоторой итерации правильного значения выходного сигнала, после нескольких итераций уйти от этого значения. Проблема динамической устойчивости подробно исследована, пожалуй, лишь для одной модели из рассматриваемой группы - нейронной сети Хопфилда.
Отсутствие строгой теории, связанной с перечисленными моделями нейронных сетей, не препятствует исследованию возможностей их применения для решения практических задач.
1. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных // Докл. АН СССР, том 108, с. 2, 1956.
2. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения // Докл. АН СССР, том 114, с. 953-956, 1957.
Повторная публикация: Нейрокомпьютер, N 1-2, с. 51-55, 1994.
3. Kolmogorov A.N. On the Representation of Continuous Functions of Many Variables by Superposition of Continuous Functions of One Variable and Addition, American Math. Soc. Transl., 28 (1963), pp. 55-63.
4. Hecht-Nielsen R. Kolmogorov's Mapping Neural Network Existence Theorem // IEEE First Annual Int. Conf. on Neural Networks, San Diego, 1987, Vol. 3, pp. 11-13.
5. Арнольд В.И. // Докл. АН СССР, том 114, N 4, 1957.
6. Muller B., Reinhart J. Neural Networks: an introduction, Springer-Verlag, Berlin Heidelberg, 1990.
7. Widrow B., Lehr M.A. 30 years of adaptive neural networks: perceptron, madaline, and backpropagation // Proceedings of the IEEE, vol. 78, No. 9, September, 1990, p. 1415-1442.