Украинский журнал телемедицины и медицинской телематики. Том 3, №2., 2005, стр 190-197.

Техническая реализация программного обеспечения для диагностики и прогнозирования синдрома жировой эмболии

И.И. Гарипов, Е.И. Гридасова, О.Г. Калинкин, М.В. Жадан

НИИ травматологии и ортопедии Донецкого государственного медицинского университета им. М. Горького, Донецк, Украина

  Жировая эмболия – тяжелое осложнение механической травмы, нередко приводящее к летальному исходу. При этом в большинстве случаев причина летальности обусловлена поздней диагностикой, которая строится на клинических, лабораторных, анамнестических данных различной значимости. При постановке диагноза наиболее часто используются: признаки ухудшения состояния после латентного периода, рентгенологическая картина легких, частота сердечных сокращений, частота дыхания, температура тела, состояние сознания, снижение сатурации, сроки и характер стабилизации переломов, содержание палочкоядерных нейтрофилов в лейкоформуле, величина жировой гиперглобулемии, содержание холестерина, наличие и качество догоспитальной помощи, длительность догоспитального периода, наличие поврежденной жировой клетчатки, петехии и др.

  Чрезвычайное разнообразие показателей и их оценок побуждает систематизировать найденные изменения и выделить наиболее достоверные признаки, приводя различные композиции диагностических показателей, каждый из которых был представлен выше. Подходы к диагностики ЖЭ можно сгруппировать следующим образом:
1. Перечисление основных признаков, на которые необходимо ориентироваться при постановке диагноза;
2. Перечисление признаков с приведением частоты встречаемости каждого;
3. Разделение признаков на главные и второстепенные;
4. Комбинации главных и второстепенных признаков с выводом формулы достаточности для диагноза.

  Построение статических моделей.

  Методы статистического исследования зависимостей:

  Данные методы различаются в зависимости от характера входных 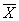и выходных 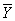переменных, которые могут быть:
- количественными, т.е. выраженными измеримыми величинами (температура, давление, вес и т.п.);
- неколичественными, которые в свою очередь разделяются на порядковые (ординальные), выражающие степень проявления какого-либо свойства (разряд рабочего, сорт продукции и т.п.);
- классификационные (номинальные), выражающие отношение объекта к какой-нибудь классификационной группе (вид растений, тип заболеваний и т.п.).

  Согласно формуле (1) определимся со значениями входных и выходных параметров. Поскольку входные параметры носят количественный характер, а выходные – классификационный, то в группу математических методов, соответствующих данной категории входят следующие статистические методы: дискриминантный анализ; кластерный анализ; метод группового учета аргументов (МГУА).

  В качестве метода построения мат. модели остановимся на дискриминантном анализе (процедура классификации). Данный метод является разделом многомерного статистического анализа, который позволяет изучать различия между двумя и более группами объектов по нескольким переменным одновременно. Дискриминантный анализ – это общий термин, относящийся к нескольким тесно связанным статистическим процедурам. Эти процедуры можно разделить на методы интерпретации межгрупповых различий – дискриминации и методы классификации наблюдений по группам.

  При интерпретации нужно ответить на вопрос: возможно ли, используя данный набор переменных, отличить одну группу от другой, насколько хорошо эти переменные помогают провести дискриминацию и какие из них наиболее информативны?

  Методы классификации связаны с получением одной или нескольких функций, обеспечивающих возможность отнесения данного объекта к одной из групп. Эти функции называются классифицирующими и зависят от значений переменных таким образом, что появляется возможность отнести каждый объект к одной из групп.

  Задачи дискриминантного анализа можно разделить на три типа. Задачи первого типа часто встречаются в медицинской практике. Допустим, что мы располагаем информацией о некотором числе индивидуумов, болезнь каждого из которых относится к одному из двух или более диагнозов. На основе этой информации нужно найти функцию, позволяющую поставить в соответствие новым индивидуумам характерные для них диагнозы. Построение такой функции и составляет задачу дискриминации.

  Второй тип задачи относится к ситуации, когда признаки принадлежности объекта к той или иной группе потеряны, и их нужно восстановить. Примером может служить определение пола давно умершего человека по его останкам, найденным при археологических раскопках.

  Задачи третьего типа связаны с предсказанием будущих событий на основании имеющихся данных. Такие задачи возникают при прогнозе отдаленных результатов лечения, например, прогноз выживаемости оперированных больных.

  Что касается предварительного отбора информативных и признаков для дальнейшей работы, то его можно проводить с помощью любого критерия различий. Удобен для этого непараметрический критерий Вилкоксона-Манна-Уитни. Ранговый Т-критерий Манна-Уитни, основаный на так называемом критерии Уилкоксона для независимых выборок, является непараметрическим аналогом t-критерия Стьюдента для сравнения двух средних значений непрерывных распределений. Данный критерий является самым строгим из непараметрических критериев.

  Порядок вычисления его таков.
1. Расположить варианты обеих выборок в возрастающем порядке, т.е. в виде одного вариационного ряда и найти в этом ряду наблюдаемое значение критерия Wнабл – сумму рангов для меньшей группы. Если численность групп одинакова, то сумму можно вычислять для любой из них.
2. Найти нижнюю критическую точку:

(2)

где nм – число членов в меньшей выборке;
nб – число членов в большей выборке;
a – заданный уровень значимости;
zкр находят из функции Лапласса по равенсту Ф(zкр)=(1-a)/2;

  Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы,то вероятность P(k1,k2) того, что событие А появится в n испытаниях от k1 до k2 раз, приближенно равна определенному интегралу

(3)

Тогда для нашего случая интеграл примет следующий вид:

(4)

  3. Находим верхнюю критическую точку по формуле:

wверх.кр.=(nм+nб+1)*nм-wнижн.кр.

(5)

Если wнижн.кр.'<'Wнабл'<'wверх.кр. – нет основанийотвергнуть нулевую гипотезу
Если Wнабл'<'wнижн.кр или Wнабл'>'wверх.кр. – нулевую гипотезу отвергают (различия статистически значимы).

  Распределение приблжается к нормальному со средним

(6)

  и стандартным отклонением

(7)

  Таким ообразом, используя данный критерий можно ответить на вопрос о том насколько хорошо эти переменные помогают провести дискриминацию и какие из них информативны.

  Процедура классификации, связанная с получением функции, обеспечивающей возможность отнесения данного объекта к одной из групп. Другими словами, мы хотим построить "модель", позволяющую лучше всего предсказать, к какой совокупности будет принадлежать тот или иной образец. Прежде чем приступить к изучению деталей различных процедур оценивания, важно уяснить, что эта разница ясна. При оценивании на основании некоторого множества данных дискриминирующую функцию, наилучшим образом разделяющую совокупности, и затем использующую те же самые данные для оценивания того, какова точность процедуры, то во многом полагаемся на волю случая. В общем случае, получают, конечно худшую классификацию для образцов, не использованных для оценки дискриминантной функции. Другими словами, классификация действует лучшим образом для выборки, по которой была проведена оценка дискриминирующей функции (апостериорная классификация), чем для свежей выборки (априорная классификация). (Трудности с (априорной) классификацией будущих образцов заключается в том, что никто не знает, что может случиться. Намного легче классифицировать уже имеющиеся образцы.) Поэтому оценивание качества процедуры классификации никогда не производят по той же самой выборке, по которой была оценена дискриминирующая функция. Если желают использовать процедуру для классификации будущих образцов, то ее следует "испытать" (произвести проверку) на новых объектах.

  Функции классификации предназначены для определения того, к какой группе наиболее вероятно может быть отнесен каждый объект. Имеется столько же функций классификации, сколько групп. Каждая функция позволяет вам для каждого образца и для каждой совокупности вычислить веса классификации по формуле:

  В этой формуле индекс i обозначает соответствующую совокупность, а индексы 1, 2, ..., m обозначают m переменных; ci являются константами для i-ой совокупности, ДК – вес переменной при вычислении показателя классификации для i-ой совокупности; xj - наблюдаемое значение для соответствующего образца j-ой переменной. Величина Si является результатом показателя классификации.

  Поэтому можно использовать функции классификации для прямого вычисления показателя классификации для некоторых новых значений.

  Как только вычислены показатели классификации для наблюдений, легко решить, как производить классификацию наблюдений. В общем случае наблюдение считается принадлежащим той совокупности, для которой получен наивысший показатель классификации.

  Алгоритм, лежащий в основании процедуры классификации вытекает из основных теорем теории вероятностей и, в частности, из основанной на них теореме Байеса (3.9), часто применяемой в вычислительной диагностике.

  При введении определенных ограничений данной диагностической задачи и начальных условий формула Байеса принимает следующий вид:

  В математической статистике подобный подход , когда накопление информации продолжается только до настижения порога предлежен А. Вальдом. Он показал, что при таком подходе требуется в среднем вдвое меньше информации для принятия решения с определенным уровнем надежности, чем при обычном классическом.

  В общем случае величины порогов определяются по следующей формуле:

  где a и b – ошибки первого и второго рода. Под ошибкой первого рода ? понимают ложную диагностику заболевания В, когда в действительности у больного заболевание А. ошибкой второго рода ? называют просмотр заболевания В и ошибочное установление диагноза А.

  Из соображений удобства вычислений целесообразно умножение отношений правдоподобия заменить соответствующим ему сложением логарифмов этих величин. Величину, которую при этом получают называют диагностическим коэффициентом. Диагностический коэффициент градации i признака xj равен:

  Фактически неравенство (10) можно изобразить иначе:

  Процедуру определения величины диагностических признаков, отыскания соответствующих им диагностических коэффициентов и их суммирования продолжают, пока правильно неравенство (13), а когда оно становится неверным, процедуру распознавания прерывают и выносят то или иное решение, в зависимости от того какой из порогов достигнут. Если при использовании всей имеющейся диагностической информации неравенство все время остается правильным (т.е. ни разу не достигается нии одиниз порогов), то выносят решение: «имеющейся информации недостаточно для принятия решения с намеченным уровнем ошибок». Все это называют правилом принятия решения при использовании процедуры классификации.

  Как было установлено ранее, получены диагностические коэффициенты ДК для каждой переменной и для каждой дискриминантной (теперь называемой также и канонической) функции. Они могут быть также проинтерпретированы обычным образом: чем больше стандартизованный коэффициент, тем больше вклад соответствующей переменной в дискриминацию совокупностей. Однако эти коэффициенты не дают информации о том, между какими совокупностями дискриминируют соответствующие функции. Вы можете определить характер дискриминации для каждой дискриминантной (канонической) функции, взглянув на средние функций для всех совокупностей. Вы также можете посмотреть, как две функции дискриминируют между группами, построив значения, которые принимают обе дискриминантные функции.

  Следовательно дискриминантный анализ - это очень полезный инструмент - для поиска переменных, позволяющих относить наблюдаемые объекты в одну или несколько реально наблюдаемых групп и для классификации наблюдений в различные группы.