
Back Propagation Neural Network for Classification of IRS-1D Satellite Images
E. Hosseini Aria, J. Amini, M.R.Saradjian Department of geomantics, Faculty of Engineering, Tehran University, Iran, Jamebozorg G., National Cartographic Center (NCC), Tehran, Iran.
РЕФЕРАТ
В этой статье исследуется пригодность использования нейронной сети обратного распространения (BPNN) для классификации отдаленно-считанных изображений. Предложен подход, состоящий из трех шагов, для классификации IRS-1D изображений. На первом шаге признаки извлечены из мер гистограмм первого порядка. Следующий шаг - классификация признаков основанных на BPNN, и на последнем шаге, результаты сравниваются с методом максимального правдоподобия (MLC). Статистические признаки в этой статье основаны на законе распределения первого порядка: среднее, стандартное отклонение, перекос, эксцесс, энергия, и энтропия. Сеть содержит 3 слоя. Извлеченные характеристики подаются на входной слой, состоящий из 18 нейронов. Нейронная сеть обратного распространения обучалась на шести классах IRS-1D, изображения основаны на известных признаках и обучение сети использовалась для классификации всех изображений. Метод рассмотренный в этой статье тестировался на регионах Ирана. IRS-1D 8-битовые зоны 2, 3 и 4 LISS-Ш были объединены с панорамными данными, для построения изображения с пространственным разрешением на 5.8 м. Экспериментальные результаты показывают, что метод BPNN более точен чем MLC и более чувствителен к обучению участков.
1. ВВЕДЕНИЕ
Основанные на биологической теории человеческого мозга, искусственные нейронные сети (NN) - модели, которые пытаются быть параллельными и моделировать функциональные возможности и процессы принятия решения человеческого мозга. Вообще, нейронная сеть относится к математическим моделям теоретически оценивающих точку зрения и умственную активность. Особенности нейронной сети, передача синапсам, нейрону, и аксонам мозга входный весов. Обработка элементов (PE) аналогична биологическому нейрону человеческого мозга. Элемент обработки имеет множество входных путей, аналогичных мозговым дендритам. Информация, переданная по этим путям, объединена в одну из разновидностей математических функций. Результат объединения этих входов - некоторый уровень внутренней активности (I) для получения PE. Объединенный вход, содержавшийся внутри PE изменяется функцией передачи (f) прежде, чем быть переданным к другому связанному PE, входные пути которого обычно взвешены (W) чувствительной синаптической силой нейронных соединений. Нейронные сети были применены во многих приложениях, таких как: автомобилестроение, космос, банковское дело, медицина, робототехника, электроника, и транспортировка. Другое применение NN - дистанционное восприятии для классификации изображений. Уже было предложено много методов классификации. Bendiktsson и др. (1990) сравнивали нейронные сети и статистические подходы для классификации многоспектральных данных. Они отметили, что обычные многомерные методы классификации не могут быть использованием в обработке мультиисходных пространственных данных из-за их часто различных свойств распределения и весов измерения. Heermann и Khazenie (1992) сравнили NN с классическими статистическими методами. Они заключили, что нейронная сеть обратного распространения может быть легко изменена, чтобы разместить больше особенностей или включить пространственную и временную информацию. Bischof и другие (1992) включили информацию о текстуре в обработку NN и пришли к выводу, что нейронная сеть в состоянии объединить другие источники знания и использовать их в классификации. Hepner и другие (1990) сравнили использование NN обратного распространения с метод максимального правдоподобия для классификации. Результат показал, что одиночное обучение по классу нейронной сети было сопоставима участку с четырех кратным обучением, при обычной классификации. Ritter и Hepner (1990) для классификации использовали модель нейронной сети с прямой связью. Результаты показали, что нейронная сеть способна отличить маленький линейный образец, который казался на изображении ТМ. В этой статье, искусственные нейронные сети используются для классификации данных, которые были получены из IRS-1D. Алгоритм обратного распространения применяется для классификации изображений. Хороший метод обучения - важная проблема в классификации IRS данных нейронной сетью. Метод TrainLM был применен при использовании нейронных сетей обратного распространения на IRS изображениях.
2 - МОДЕЛЬ НЕЙРОННОЙ СЕТИ
Сначала, в этом разделе представлена архитектура алгоритма обратного распространения. Обратное распространение было создано для обобщения правила обучения Widrow-Hoff многослойной сети и нелинейной дифференцируемой функции передачи. Входные вектора и соответствующие целевые вектора используются для обучения сети, пока они способны приближать функцию, ассоциируемые входные вектора с определенными выходными векторами; или классифицировать входные вектора соответствующим способом как определено в обучении. Сети со смещением, сигмоидальным слоем и линейным выходным слоем способны аппроксимировать любую функцию с конечным числом разрывов. Алгоритм обратного распространения состоит из двух частей; с прямой связью и обратной. Прямая связь содержит создание сети с прямой связью, калибрование веса, моделирование и обучение сети. Веса и погрешности сети обновляются в обратной направлении. (Rumelhart, 1986), Отдельная сеть с 4 входами показана на рисунке 1.

Сети с прямой связью часто имеет один или более скрытых слоев из сигмоидальных нейронов, сопровождаемых выходным слоем линейных нейронов. Многослойные нейроны с нелинейной функцией передачи позволяют сети изучать нелинейные и линейные отношения между входными и выходными векторами. Линейный выходной слой позволяет сети производить значения вне диапазона от -1 до +1 (иллюстрация 2).
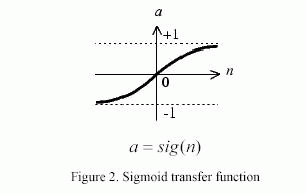
С другой стороны, если мы хотим ограничить выход сети в диапазоне от 0 до 1, тогда выходной слой должен использовать логорифмическую сигмоидальную функцию передачи. Перед обучением сети с прямой связью веса и погрешности должны быть инициализированы. Как только веса сети и погрешности измерений инициализированы, сеть готова к обучению. Мы использовали случайные числа около нуля, для инициализации весов и погрешностей в сети. Процесс обучения требует ряда надлежащих входов и целевых выходов. В течение обучения, веса и погрешности сети многократно настраиваются, чтобы минимизировать функцию выполнения сети. По умолчанию выполнение функции для сети с прямой связью находятся средние квадратичные ошибки; средние квадратичные ошибки между выходами сети и целевой выходами.
2.1. Модель обучения
Есть несколько алгоритмов обучения для сетей с прямой подачей. Все эти алгоритмы используют метод градиентного спуска выполнения функции, чтобы решить, как отрегулировать веса и минимизировать работу. Градиент определяется, используя технику, называемую обратным распространением, которое включает вычислительное выполнение, назад через сеть. Самая простая реализация обратного распространения, изучающего обновления веса и погрешности сети в направлении, в котором выполнение функция уменьшается быстрее. Повторение этого алгоритма может быть написано
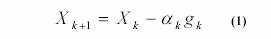

Есть два различных пути, которыми может быть осуществлен алгоритм градиентного спуска: дифференциальный момент и пакетный режим. В дифференциальном моменте, вычисляется градиент, и веса обновляются после того, как каждый вход применен к сети. В пакетном режиме все входы применены к сети прежде, чем веса обновлены. В этой статье, мы использовали Levinberg-Marquardt обучение (trainLM) (Hagan, Menhaj, 1994). Он быстрее и более точен, чем стандартный алгоритм обучения обратного распространения. Он может сходиться от десяти до ста раз быстрее чем стандартный алгоритм с использованием правила дельты. Этот алгоритм работает в пакетном режиме и призван использовать обучение, как методы квази Ньютона, алгоритм Levenberg-Marquardt был разработан, чтобы приблизиться ко второму порядку обучения, не имея необходимость вычислять матрицу Hessian. Когда функция работы имеет форму суммы квадратов (как типично при обучении в сетях с прямой подачей), тогда матрица Hessian может быть аппроксимирована как
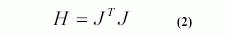
и градиент может быть вычислен как
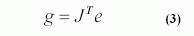
где J = матрица Якобиан, которая содержит первые производные ошибок сети относительно весов и погрешностей
e = вектор ошибок сети, Якобиан может быть вычислен через стандартную технику обратного распространения, которая намного менее сложна чем вычисление матрицы Hessian. Алгоритм Levenberg-Marquardt использует это приближение для матрицы Hessian в следующем Newton-like обновлении:

Когда скаляр µ - ноль, это только метод Ньютона, используют аппроксимацию матрицы Hessian. Когда µ является большим, метод становится градиентным спуском с маленьким размером шага. Метод Ньютона быстрее и более точно минимизирует ошибку, таким образом цель состоит в том, чтобы перейти к методу Ньютона как можно быстрее. Таким образом, µ уменьшается после каждого успешного шага (сокращение выполнения функции) и увеличивается только тогда, когда предварительный шаг увеличил бы выполнение функции. Таким образом, выполнение функции будет всегда уменьшаться при каждом повторении алгоритма.
3. ОБЛАСТИ ИССЛЕДОВАНИЯ И ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
В этой статье блок-схема показана на рисунке. Эта блок-схема состоит из 3 шагов: выделение признаков, проектирование сети, обучение и классификация.

3.1. Выделение признаков
Классификацию многоспектрального дистанционного восприятия данных можно рассмотривать как картографию, F, из многомерного пространства серого в дискретное векторное пространство классов признаков данных

где: a, b, c, d, … = значения серого в пикселах в различных спектральных полосах; A, B, C, … = характеристики классов; M*N = общее количество пикселов в изображении, в любой из спектральных полос. Большинство основ всех характеристик изображения - некоторые меры амплитуды изображения в элементах светимости, спектральные значения, и т.д. Один из самых простых способов извлечения особенностей текстуры изображения - использование распределения вероятностей первого порядка амплитуды квантованного изображения. Их вообще легко вычислять и в большей степени эвристически. Оценка первого порядка гистограммы p(b) проста
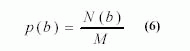
где b = серый уровень на изображении
M = представить общего количества пикселов в соседнем окне, сосредоточенном об ожидаемом пикселе
N (b) = число пикселов серого b в том же самом окне, что 0 <=b <=L-1
Тогда следующие меры были извлечены при использовании первого порядка распределения вероятностей.
Среднее:
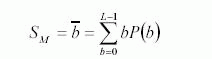
Стандартное отклонение:
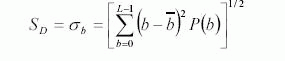
Перекос:

Эксцесс:

Энергия:
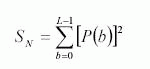
Энтропия:
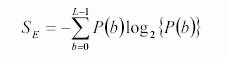
Первые две особенности - среднее и стандартное отклонение яркостей пикселов в пределах окна изображения. Затем, чтобы получить информацию на форме распределения значения яркостей в пределах окна, определяется перекос и эксцесс. Перекос, характеризует степень асимметрии распределения яркости вокруг средней яркости. Если перекос отрицателен, данные распространяются больше налево от среднего чем направо. Если перекос положителен, данные распространены больше направо. Эксцесс, мера относительного пика или колебания распределения интенсивности относительно нормального распределения. Эксцесс нормального распределения - 3. Распределение, которые являются более склонными к изолированной части чем нормальное распределение, имеет эксцесс, больше чем 3; Распределение, которые менее склонные к изолированной части, имеет эксцесс меньше чем 3. Наконец определяется энергия и энтропия. Энергия используют для исследования степени емкости (повторенные переходы) в определенной полосе частоты. Энтропия - общее понятие во многих областях, главным образом при обрабатке сигналов (Coifman1992).
3.2 Проект сети
В этой статье, разработана трехслойная сеть. Входной вектор и соответствующий желаемый выход рассмотрим сначала. Вход распространен вперед через сеть, чтобы вычислить выходной вектор. Выходной вектор - по сравнению с желаемым выходом и ошибки определены. Ошибки распространяются назад через сеть от выходного к входному слою. Процесс повторяется пока ошибки не будут минимальными. Входной слой сети содержит 18 нейронов, соответствующий 3 полосам изображения IRS-1D (шесть признаков для пиксела в каждой полосе). Выходной слой содержит 6 нейронов, соответствующих 6 предопределенным категориям покрытия земли для классификации. Проектируя нейронную сеть, важно и трудно определить параметр - число нейронов в скрытых слоях (Bischof и др., 1992). Скрытый слой ответственен за внутреннее представление данных и информационного передачу входных и выходных слоев. Если слишком мало нейронов в скрытом слое, сеть, возможно, не содержит достаточной степени свободы сформировать представление. Если слишком много определено нейронов, сеть может переобучится (Heermann и др., 1999). Поэтому, оптимальный проект для числа нейронов в скрытом слое – повторение. В этом исследовании, мы использовали один скрытый слой с множеством различных нейронов, чтобы определить подходящую сеть. Таблица 1 показывает ошибку сети для четырех случаев.
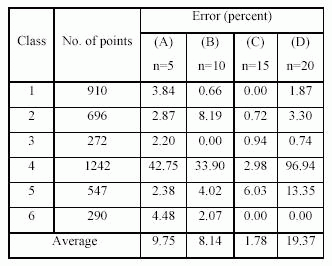
Таблица1. Четыре сети с различными нейронами в скрытом слое. 'n' - число нейронов в скрытом слое.
Как видно в таблице 1, сеть с 15 нейронами в скрытом слое имеет минимальную ошибку, таким образом это - лучший вариант для проектирования сеть в таком виде. Она также быстро обучается как другие.