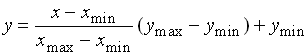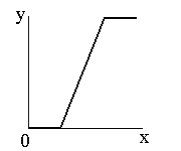Содержание
- Общие понятия фильтрации изображений
- Масочная фильтрация
- Нелинейная фильтрация
- Бинаризация
- Линейное контрастирование
- Пилообразное контрастирование
Общие понятия фильтрации изображений
Изображения, сформированные различными оптико-электронными системами и
зарегистрированные с помощью разнообразных приёмников искажаются действием помех
различного характера. Искажения изображения вносятся всеми компонентами
изображающего прибора, начиная с осветительной системой (например,
неравномерность освещенности предмета). Искажения, которые вносит оптическая
система, известны еще на этапе её проектирования и называются аберрации.
Искажения, которые вносят электронные приёмники излучения, например ПЗС-матрицы,
называются электронный шум. Помехи затрудняет визуальный анализ изображения и
его автоматическую обработку.
Ослабление действия помех достигается фильтрацией. При фильтрации яркость
(сигнал) каждой точки исходного изображения, искаженного помехой, заменяется
некоторым другим значением яркости, которое признается в наименьшей степени
искаженным помехой. Для выполнения фильтрации необходимо выработать принципы
таких преобразований, которые основываются на том, что интенсивность изображения
изменяется по пространственным координатам медленнее, чем функция помех. В
других случаях, наоборот, признаком полезного сигнала являются резкие перепады
яркости.
В методах фильтрации при оценке реального сигнала в некоторой точке кадра
принимают во внимание некоторое множество (окрестность) соседних точек,
воспользовавшись определенной похожестью сигнала в этих точках. Понятие
окрестности является достаточно условным. Окрестность может быть образована лишь
ближайшими по кадру соседями, но могут быть окрестности, содержащие достаточно
много и достаточно сильно удаленных точек кадра. В этом случае, степень влияния
(вес) далеких и близких точек на решения, принимаемые фильтром в данной точке
кадра, будет совершенно различной. Таким образом, идеология фильтрации
основывается на рациональном использовании данных как из рабочей точки, так и из
ее окрестности.
При решении задач фильтрации используют вероятностные модели изображения и
помехи, и применяют статистические критерии оптимальности. Это связано со
случайным характером помехи и стремлением получить минимальное в среднем отличие
результата обработки от идеального сигнала. Многообразие методов и алгоритмов
фильтрации связано с большим разнообразием математических моделей сигналов и
помех, а также различными критериями оптимальности.
Пусть 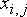 – значение яркости изображения – полезного сигнала на
пересечении i-ой строки и j-го столбца,
а наблюдаемое на входе фильтра изображение описывается моделью: – значение яркости изображения – полезного сигнала на
пересечении i-ой строки и j-го столбца,
а наблюдаемое на входе фильтра изображение описывается моделью:
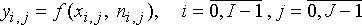
Здесь 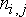 – значение помехи в точке с координатами
(i,j), f() – функция, описывающая
взаимодействие сигнала и помехи, а I и J – число строк и
столбцов в кадре соответственно. – значение помехи в точке с координатами
(i,j), f() – функция, описывающая
взаимодействие сигнала и помехи, а I и J – число строк и
столбцов в кадре соответственно.
На рисунке 1 показаны примеры окрестностей различных типов, изображенные в
виде совокупностей точек. Центром окрестностей, рабочей точкой, в которой
осуществляется обработка, является точка с координатами
(i,j).
Рисунок 1 Примеры окрестностей различных видов
В зависимости от типа окрестности различают каузальную (а), некаузальную (б)
и полукаузальную (в) фильтрацию изображений. Понятие каузальности
(причинно-следственной зависимости) связывают с соотношением координат текущей
точки и точек, входящих в окрестность. Если обе координаты (номер строки и номер
столбца) всех точек окрестности не превышают соответствующих координат текущей
точки, то окрестность и использующая ее обработка называются
каузальными. Если точки окрестности удовлетворяют принципу
каузальности, фильтрация, опирающаяся на использование такой окрестности,
называется некаузальной. Если среди точек окрестности есть точки,
координаты которых не превышают рабочую точку в одном направлении, но превышают
её в другом, то фильтрация является полукаузальной фильтрацией.
При линейной фильтрации выходной эффект определяется линейной комбинацией
входных данных:
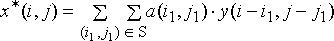 . .
В этом выражении 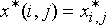 – результат фильтрации полезного сигнала в точке кадра с
координатами (i,j), S – множество точек,
образующих окрестность, – результат фильтрации полезного сигнала в точке кадра с
координатами (i,j), S – множество точек,
образующих окрестность,  – весовые коэффициенты, совокупность которых представляет
собой двумерную импульсную характеристику (ИХ). Если область S
конечна, то импульсная характеристика имеет конечную длину и фильтр называется
КИХ-фильтром. В противном случае импульсная характеристика имеет бесконечную
длину, а фильтр называется БИХ-фильтром. Импульсная характеристика не зависит от
координат точки, в которой определяется выходной эффект. Процедуры обработки
изображений, обладающие свойством независимости от координат, называются
однородными (изопланатичными). – весовые коэффициенты, совокупность которых представляет
собой двумерную импульсную характеристику (ИХ). Если область S
конечна, то импульсная характеристика имеет конечную длину и фильтр называется
КИХ-фильтром. В противном случае импульсная характеристика имеет бесконечную
длину, а фильтр называется БИХ-фильтром. Импульсная характеристика не зависит от
координат точки, в которой определяется выходной эффект. Процедуры обработки
изображений, обладающие свойством независимости от координат, называются
однородными (изопланатичными).
Наиболее распространенным критерием оптимальности, применяемым для оценки
качества обработки, является критерий минимума среднего квадрата ошибок.
Применительно к фильтрации запишем его выражение в виде:
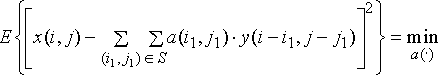
где 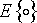 – символ математического ожидания. Отыскание оптимального
фильтра заключается в определении его ИХ таким образом, чтобы средний квадрат
ошибки – символ математического ожидания. Отыскание оптимального
фильтра заключается в определении его ИХ таким образом, чтобы средний квадрат
ошибки 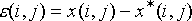 ,
выражающей различие между сигналом и оценкой, формируемой фильтром, был
минимальным. ,
выражающей различие между сигналом и оценкой, формируемой фильтром, был
минимальным.
Очень часто при обработке стремятся сохранить
среднюю яркость изображения. Математическое ожидание от обеих частей уравнения
фильтрации можно записать следующим образом:
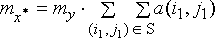
где принято, что средняя яркость 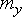 входного изображения входного изображения 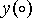 не зависит от
координат и, как результат, получено, что и средняя яркость не зависит от
координат и, как результат, получено, что и средняя яркость 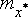 выходного изображения выходного изображения 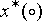 также постоянна во всех
точках кадра. Сохранить среднюю яркость изображения удается при выполнении
равенства также постоянна во всех
точках кадра. Сохранить среднюю яркость изображения удается при выполнении
равенства
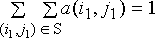
которое является дополнительным требованием к импульсной характеристике
фильтра.
Потенциально наилучшие результаты фильтрации, достигаются при использовании
некаузального принципа, поскольку этот принцип основан на применении абсолютно
всех исходных данных при обработке каждой точки кадра.
Масочная фильтрация
В практике цифровой обработки изображений широко используется некаузальная
масочная фильтрация. Ее линейная разновидность является одним из
вариантов двумерной КИХ-фильтрации. В этом случае функцию 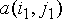 называют маской,
которая представляет собой весовых коэффициентов, заданных во всех точках
окрестности, обычно симметрично окружающих рабочую точку кадра. Распространенным
видом окрестности, часто применяемым на практике, является квадрат размером 3 на
3 элемента с рабочим элементом в центре. Применяют различные разновидности масок, одним из эвристических
вариантов является равномерная маска, когда все девять весовых коэффициентов
которой равны 1/9. Такой выбор коэффициентов отвечает условию сохранения
средней яркости и центрировать изображение в процессе обработки не
требуется. называют маской,
которая представляет собой весовых коэффициентов, заданных во всех точках
окрестности, обычно симметрично окружающих рабочую точку кадра. Распространенным
видом окрестности, часто применяемым на практике, является квадрат размером 3 на
3 элемента с рабочим элементом в центре. Применяют различные разновидности масок, одним из эвристических
вариантов является равномерная маска, когда все девять весовых коэффициентов
которой равны 1/9. Такой выбор коэффициентов отвечает условию сохранения
средней яркости и центрировать изображение в процессе обработки не
требуется.
Для выполнения такой процедуры фильтрации библиотека IPL предоставляет
функцию iplBlur, которая имеет следующий
прототип.
void iplBlur(IplImage*
srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int anchorY);
где srcImage – указатель на
исходное изображение, а dstImage –
указатель на изображение, в котором будет сохраняться результат. Остальные
параметры используются для формирования маски: nCols - количество столбцов, nRows – количество строк в окрестности рабочей
точки (в маске), anchorX и anchorY – координата центра маски. В системе
координат маски ее верхнему левому углу соответствует точка с координатами
(0,0), а её правому нижнему углу соответствует точка с координатами (nCols-1,
nRows-1). Таким образом для маски размером 3 на 3 должна быть координата центра
(1,1). Действие этой функции подобно размытию или усреднению интенсивности
изображения.
Но основная функция библиотеки IPL, с помощью которой можно выполнять
фильтрацию с произвольными масками называется iplConvolve2D, так как выполняет непосредственно
процедуру свертки изображения с маской. Для выполнения свертки необходимо
выполнить подготовку маски (или ядра свертки) с помощью функции iplCreateConvKernel. Получить ядро сверки, которое
будет использоваться при выполнений свертки можно с помощью функции iplGetConvKernel. А после выполнения свертки ядро
должно быть удалено с помощью функции iplDeleteConvKernel. Перечисленные выше функции
имеют следующие прототипы:
IplConvKernel* iplCreateConvKernel(int nCols, int nRows, int anchorX, int anchorY, int* values, int
nShiftR);
void iplGetConvKernel(IplConvKernel*
kernel, int* nCols, int*
nRows, int* anchorX, int*
anchorY, int** values, int* nShiftR);
void
iplDeleteConvKernel(IplConvKernel* kernel);
Аргументы nCols и nRows определяют соответственно количество столбцов
и строк в окрестности рабочей точки (в маске), anchorX и anchorY – координата центра маски. Аргумент
values – представляет собой ссылку
на массив, в элементах которого сохранены значения весовых коэффициентов маски.
Аргумент nShiftR определяет количество
бит для сдвига вправо каждого значения изображения-результата. Аргумент типа
IplConvKernel представляет собой
структуру, в которой хранятся все параметры необходимые для выполнения
фильтрации.
Функция для выполнения свертки (и соответственно масочной фильтрации) имеет
следующий прототип:
void
iplConvolve2D(IplImage* srcImage, IplImage* dstImage, IplConvKernel** kernel,
int nKernels, int
combineMethod);
где srcImage – как всегда
указатель на исходное изображение, а dstImage – указатель на изображение, в котором
будет сохраняться результат. Аргумент kernel – указатель на массив указателей ядер
свертки. Количество элементов в этом массиве определяется следующим аргументом
nKernels, а то как они будут
использоваться определяется последним аргументом combineMethod, который может быть равен одному из
следующих значений:
IPL_SUM // результат сверток
суммируется
IPL_SUMSQ // суммируются квадраты
результатов
IPL_SUMSQROOT // суммируются квадраты
результатов а затем вычисляется корень квадратный
IPL_MAX // Выбирается максимальный результат
IPL_MIN // Выбирается минимальный результат
Если аргумент nKernels=1, то аргумент
combineMethod игнорируется, так как
выполняется одна свертка, результат которой записывается в dstImage. Используя всевозможные ядра фильтрации
можно решать не только задачу фильтрации, но и многие другие задачи обработки
изображений. Итак, процедура выполнения масочной фильтрации по месту может быть
реализована следующим образом:
void
MaskFiltering(IplImage* img)
{
// Скопировать
исходное изображение во временное
IplImage*
tmp = iplCloneImage(img);
// Подготовить массив ядра
свертки
int one[9]
= {1,-1,1,-1,1,-1,1,-1,1};
// Создать ядро
свертки
IplConvKernel*
kernel=iplCreateConvKernel(3, 3, 1, 1, one, 0);
//
Выполнить свертку
iplConvolve2D(img, tmp,
&kernel, 1, IPL_SUM);
// Удалить ядро
свертки
iplDeleteConvKernel(kernel);
// Освободить память исходного
изображения
iplDeallocate(img,
IPL_IMAGE_ALL);
// Скопировать результат в исходное
изображение
img=iplCloneImage(tmp);
// Освободить память временного
изображения
iplDeallocate(tmp,
IPL_IMAGE_ALL);
}
Библиотека IPL предоставляет возможность выполнить раздельную свертку по
строкам и столбцам с помощью функции, которая имеет прототип:
void iplConvolveSep2D
(IplImage* srcImage, IplImage* dstImage, IplConvKernel* xKernel, IplConvKernel*
xKernel);
где srcImage – указатель на
исходное изображение, а dstImage –
указатель на изображение, в котором будет сохраняться результат. Аргументы
xKernel и yKernel принимают ядра для выполнения свертки по
строкам и столбцам соответственно. Один из этих аргументов может быть равен
NULL.
Библиотека IPL также предоставляет возможность выполнить свертку изображения
с ранее определенными масками. Это можно сделать с использованием функции,
которая имеет следующий прототип:
int
iplFixedFilter(IplImage* srcImage, IplImage* dstImage, IplFilter
filter);
где srcImage – указатель на
исходное изображение, а dstImage –
указатель на изображение, в котором будет сохраняться результат. Аргумент
filter определяет ядро свертки и может
принимать следующие значения:
IPL_PREWITT_3x3_V |
Градиентный фильтр Превитта (вертикальный) |
-1 0 1
-1 0 1
-1 0 1 |
IPL_PREWITT_3x3_H |
Градиентный фильтр Превитта (горизонтальный) |
1 1 1
0 0 0
-1 -1 -1 |
IPL_SOBEL_3x3_V |
Градиентный фильтр Собеля (вертикальный) |
-1 0 1
-2 0 2
-1 0 1 |
IPL_SOBEL_3x3_H |
Градиентный фильтр Собеля (горизонтальный) |
1 2 1
0 0 0
-1 -2 -1 |
IPL_LAPLACIAN_3x3 |
Фильтр высоких частот Лапласа (3X3) |
-1 -1 -1
-1 8 -1
-1 -1 -1 |
IPL_LAPLACIAN_5x5 |
Фильтр высоких частот Лапласа (5X5) |
-1 -3 -4 -3 -1
-3 0 6 0 -3
-4 6 20 6 -4
-3 0 6 0 -3
-1 -3 -4 -3 -1 |
IPL_GAUSSIAN_3x3 |
Фильтр низких частот Гаусса (3X3) |
1 2 1
2 4 2
1 2 1 |
IPL_GAUSSIAN_5x5 |
Фильтр низких частот Гаусса (5X5) |
2 7 12 7 2
7 31 52 31 7
12 52 127 52 12
7 31 52 31 7
2 7 12 7 2 |
IPL_HIPASS_3x3 |
Фильтр высоких частот (3X3) |
-1 -1 -1
-1 8 -1
-1 -1 -1 |
IPL_HIPASS_5x5 |
Фильтр высоких частот (5X5) |
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 24 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1 |
IPL_SHARPEN_3x3 |
Фильтр повышения резкости |
-1 -1 -1
-1 16 -1
-1 -1 -1 |
Процедура выполнения фильтрации по месту с заранее определенным ядром может
быть реализована следующим образом:
void
FixedFilter(IplImage* img, IplFilter filter)
{
//
Скопировать исходное изображение во
временное
IplImage* tmp =
iplCloneImage(img);
// Выполнить
фильтрацию
iplFixedFilter(img, tmp,
filter);
// Освободить память исходного
изображения
iplDeallocate(img,
IPL_IMAGE_ALL);
// Скопировать результат в исходное
изображение
img =
iplCloneImage(tmp);
// Освободить память временного
изображения
iplDeallocate(tmp,
IPL_IMAGE_ALL);
}
Нелинейная фильтрация
Все линейные алгоритмы фильтрации приводят к сглаживанию резких перепадов
яркости изображений, прошедших обработку. Линейные процедуры являются
оптимальными при гауссовском распределении сигналов, помех и наблюдаемых данных.
Обычно этому условию отвечают шумовые помехи на изображениях, поэтому при их
подавлении линейные алгоритмы имеют высокие показатели. А если, например, задача
обработки изображения состоит в выявлении границ объекта, то линейная фильтрация
не подходит для ее решения.
Реальные изображения не подчиняются данному распределению вероятностей
(разнообразные перепады яркости на границах, переходы от одной текстуры к другой
и т. п.). Приходится иметь дело с изображениями, искаженными помехами других
типов. Одной из них является импульсная помеха. При ее воздействии на
изображении наблюдаются белые или (и) черные точки, хаотически разбросанные по
кадру. Применение линейной фильтрации в этом случае неэффективно - каждый из
входных импульсов ( по сути - дельта-функция) дает отклик в виде импульсной
характеристики фильтра, а их совокупность способствует распространению помехи на
всю площадь кадра.
Удачным решением перечисленных проблем является применение медианной
фильтрации. Отметим, что медианная фильтрация представляет собой эвристический
метод обработки, ее алгоритм не является математическим решением строго
сформулированной задачи. Также как и в методе масочной фильтрации, при
применении медианного фильтра происходит последовательная обработка каждой точки
кадра, а для вычисления оценки используется некоторая окрестность (окно).
Наиболее часто применяются варианты окон в виде креста и в виде квадрата.
Размеры окна изменяются в зависимости от задаче и характера изображения. Отсчеты
изображения, оказавшиеся в пределах окна, образуют рабочую выборку текущего
шага.
Обозначим рабочую выборку в виде одномерного массива 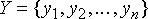 ; число его элементов
равняется размеру окна, а их расположение произвольно. Обычно применяют окна с
нечетным числом точек n (это автоматически обеспечивается при центральной
симметрии апертуры и при вхождении самой центральной точки в ее состав). Если
упорядочить последовательность ; число его элементов
равняется размеру окна, а их расположение произвольно. Обычно применяют окна с
нечетным числом точек n (это автоматически обеспечивается при центральной
симметрии апертуры и при вхождении самой центральной точки в ее состав). Если
упорядочить последовательность 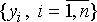 по возрастанию, то ее медианой (средним
значением) будет тот элемент выборки, который занимает центральное положение в
этой упорядоченной последовательности. Полученное таким образом число и является
продуктом фильтрации для текущей точки кадра. Понятно, что результат такой
обработки в самом деле не зависит от того, в какой последовательности
представлены элементы изображения в рабочей выборке. Формальное обозначение
описанной процедуры выглядит следующим образом: по возрастанию, то ее медианой (средним
значением) будет тот элемент выборки, который занимает центральное положение в
этой упорядоченной последовательности. Полученное таким образом число и является
продуктом фильтрации для текущей точки кадра. Понятно, что результат такой
обработки в самом деле не зависит от того, в какой последовательности
представлены элементы изображения в рабочей выборке. Формальное обозначение
описанной процедуры выглядит следующим образом:
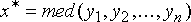
>Предположим, что апертура фильтра находится вблизи границы, разделяющей
светлый и темный участки изображения, при этом ее центр располагается в области
темного участка. Тогда, вероятнее всего, рабочая выборка будет содержать большее
количество элементов с малыми значениями яркости, и, следовательно, медиана
будет находиться среди тех элементов рабочей выборки, которые соответствуют этой
области изображения. Ситуация меняется на противоположную, если центр апертуры
смещен в область более высокой яркости.
Рассмотрим пример. Предположим, что выборка имеет вид: {136, 110, 99, 45,
250, 55, 158, 104, 75}, а элемент 250, расположенный в ее центре, соответствует
текущей точке фильтрации 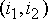 . Упорядоченная по возрастанию выборка имеет при этом вид: {45,
55, 75, 99, 104, 110, 136, 158, 250}, следовательно, получаем . Упорядоченная по возрастанию выборка имеет при этом вид: {45,
55, 75, 99, 104, 110, 136, 158, 250}, следовательно, получаем 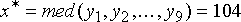 . Как видим, влияние
соседей на результат фильтрации в текущей точке привело к игнорированию
импульсного выброса яркости, что следует рассматривать как эффект фильтрации.
Если импульсная помеха не является точечной, а покрывает некоторую локальную
область, то она также может быть подавлена. Это произойдет, если размер этой
локальной области будет меньше, чем половина размера окна. Поэтому для
подавления импульсных помех, поражающих локальные участки изображения, следует
увеличивать размеры окна. . Как видим, влияние
соседей на результат фильтрации в текущей точке привело к игнорированию
импульсного выброса яркости, что следует рассматривать как эффект фильтрации.
Если импульсная помеха не является точечной, а покрывает некоторую локальную
область, то она также может быть подавлена. Это произойдет, если размер этой
локальной области будет меньше, чем половина размера окна. Поэтому для
подавления импульсных помех, поражающих локальные участки изображения, следует
увеличивать размеры окна.
Аналогично, строятся фильтры максимумов и минимумов.
Для выполнения медианной фильтрации библиотека IPL предоставляет функцию
iplMedianFilter, которая имеет следующий
прототип:
void
iplMedianFilter(IplImage* srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int
anchorY);
где srcImage – указатель на
исходное изображение, а dstImage –
указатель на изображение, в котором будет сохраняться результат, nCols – размер окна по горизонтали, nRows – размер окна по вертикали, anchorX и anchorY – координата рабочей точки в системе
координат окна.
Для выполнения нелинейной фильтрации максимумов и минимумов библиотека IPL
предоставляет функции, которые имеют следующие прототипы:
void
iplMaxFilter(IplImage* srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int
anchorY);
void iplMinFilter(IplImage* srcImage,
IplImage* dstImage, int nCols, int nRows, int anchorX, int anchorY);
где srcImage – указатель на
исходное изображение, а dstImage –
указатель на изображение, в котором будет сохраняться результат, nCols – размер окна по горизонтали, nRows – размер окна по вертикали, anchorX и anchorY – координата рабочей точки в системе
координат окна.
void
NonlinearFilter(IplImage* img, int
filter)
{
// Скопировать исходное изображение во
временное
IplImage* tmp = iplCloneImage
(img);
switch(filter)
{
case
-1:
{
// Выполнить
нелинейную фильтрацию
минимумов
iplMinFilter(m_img,
tmp, 3, 3, 1,
1);
break;
}
case
0:
{
// Выполнить
нелинейную медианную
фильтрацию
iplMedianFilter(m_img,
tmp, 3, 3, 1,
1);
break;
}
case
1:
{
// Выполнить
нелинейную фильтрацию
максимумов
iplMaxFilter(m_img,
tmp, 3, 3, 1,
1);
break;
}
}
// Освободить память исходного
изображения
iplDeallocate(img, IPL_IMAGE_ALL
);
// Скопировать результат в исходное
изображение
img=iplCloneImage(tmp);
// Освободить память временного
изображения
iplDeallocate(tmp, IPL_IMAGE_ALL
);
}
Для медианной фильтрации цветных изображений в библиотеке IPL предусмотрена
специальная функция:
void
iplColorMedianFilter(IplImage* srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int
anchorY);
где srcImagedstImage – указатель на
изображение, в котором будет сохраняться результат, nColsnRowsanchorX и
anchorY
Функция iplMedianFilter обрабатывет
цветовые плоскости изображения отдельно, вследствие чего цветовая корреляция
изображения до и после фильтрации отсутствует. Функция iplColorMedianFilter вычисляет медиану используя
следующее значение (цветовое расстояние): abs(R(i) - R(j)) + abs(G(i) - G(j)) +
abs(B(i) - B(j)), где
Бинаризация
Простейшим методом препарирования изображений является бинаризация.
Это преобразование заключается в превращении изображения в двухцветное
черно-белое. Главным параметром такого преобразования является порог –
значение, которое будет критерием проверки интенсивности точки изображения.
Функция бинаризации представлена на рисунке 2.
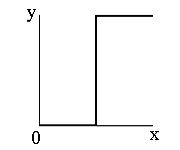
Рисунок 2. Функция бинаризации
В библиотеке IPL для выполнения бинаризации используется функция iplThreshold, которая имеет следующий
прототип:
void
iplThreshold(IplImage* srcImage, IplImage* dstImage, int threshold);
где srcImage – указатель на
исходное изображение, а dstImage –
указатель на изображение, в котором будет сохраняться результат. Аргумент
threshold задает пороговое значение.
Функция бинаризации может выполняться по месту, то есть ее использование никаких
затруднений не вызывает.
Иногда при обработке приходится иметь дело с изображениями, хранимыми как
полутоновые, но по своему содержанию мало отличающимися от бинарных. К ним
относятся текст, штриховые рисунки, чертежи, изображение отпечатка пальца.
Замена исходного полутонового изображения бинарным препаратом решает две
основные задачи. Во-первых, достигается большая наглядность при визуальном
восприятии, чем у исходного изображения. Во-вторых, ощутимо сокращается объем
запоминающего устройства для хранения изображения, поскольку бинарный препарат
для записи каждой точки бинарного изображения требует лишь 1 бит памяти, в то
время как полутоновое изображение для решения той же задачи при наиболее часто
применяемом формате представления - 8 бит.
Для реализации других методов препарирования изображений необходимо
познакомиться со структурой IplLUT и
правилами работы с ней. Вообще, структура IplLUT предназначена для хранения информации о
функции препарирования. Она имеет следующий состав:
typedef struct
_IplLUT
{
int num;
// количество ключевых
значений
int* key;
// указатель на массив ключевых
значений
int*
value; // указатель на массив значений (либо величина
сдвига, либо непосредствено новые значения
интенсивности)
int*
factor; // указатель на массив дополнительных
множителей
int
interpolateType; // тип преобразования
}
IplLUT;
Массив ключевых значений должен иметь размер равный num. Массивы value и factor должны иметь размер num-1. Параметр interpolateType может быть равен IPL_LUT_LOOKUP или IPL_LUT_INTER.
Если тип преобразования IPL_LUT_LOOKUP, то интенсивность исходного
изображения D из диапазона
key[0] <= D < key[1]
после преобразования будет равна значению value[0], из диапазона key[1] <= D < key[2] – value[1] и
так далее.
Если тип преобразования IPL_LUT_INTER, то интенсивность исходного
изображения D из диапазона key[0] <= D < key[1] после
преобразования будет равна значению линейно интерполированному значению:
value[0] + [(value[1] – value[0]) / (key[1] –
key[0])] * (D – key[0]).
Значение (value[1] – value[0]) / (key[1] –
key[0]) соответствует наклону интерполирующей линии в этой
точке и должно быть заранее вычислено и сохранено в factor[0]. Формулу, которая
используется библиотекой, можно записать так: D_
= value[i] + factor[i] * (D – key[i]).
К сожалению, библиотека IPL не предоставляет никаких функций для созданий и
манипулирования структурой IplLUT,
поэтому создадим свои:
void CreateLUT(IplLUT*
lut)
{
lut->key = new
int[lut->num];
lut->value = new
int[lut->num-1];
lut->factor = new
int[lut->num-1];
for(int i=0; i<lut->num;
i++)
{
lut->key[i]
= i;
}
}
void DeleteLUT(IplLUT*
lut)
{
delete []
lut->key;
delete []
lut->value;
delete []
lut->factor;
}
Функция для выполнения препарирования изображений может быть реализована
следующим образом:
void Preparing(IplImage*
img, int type)
{
//
Создание lookup-таблиц
IplLUT lut[3] =
{{256 + 1, NULL, NULL, NULL,
IPL_LUT_INTER},
{256+1,
NULL, NULL, NULL,
IPL_LUT_INTER},
{256+1, NULL,
NULL, NULL, IPL_LUT_INTER}};
// Создание и
инициализация массива указателей на
lookup-таблицы
IplLUT*
plut[3];
plut[0] =
&lut[0];
plut[1] =
&lut[1];
plut[2] = &lut[2];
// Инициализация членов
lookup-таблиц
CreateLUT(plut[0]);
CreateLUT(plut[1]);
CreateLUT(plut[2]);
switch(type)
{
// Подготовка
lookup-таблиц
...
}
//
Препарирование
iplContrastStretch(img, img,
plut);
// Удаление членов
lookup-таблиц
DeleteLUT(plut[0]);
DeleteLUT(plut[1]);
DeleteLUT(plut[2]);
}
При реализации некоторых методов препарирования бывает необходима
дополнительная информация об изображении. Её можно получить с использованием
гистограммы, для вычисления которой предусмотрена специальная функция:
void
iplComputeHisto(IplImage* srcImage, IplLUT** lut);
где srcImage – изображение для
которого будет вычисляться гистограмма, а lut – массив указателей на структуры LUT
(один указатель на каждый канал).
Линейное контрастирование
Задача контрастирования связана с улучшением согласования динамического
диапазона изображения и экрана, на котором выполняется визуализация. Если для
цифрового представления каждого отсчета изображения отводится 1 байт (8 бит)
запоминающего устройства, то входной или выходной сигналы могут принимать одно
из 256 значений. Обычно в качестве рабочего используется диапазон 0...255; при
этом значение 0 соответствует при визуализации уровню черного, а значение
255 – уровню белого. Предположим, что минимальная и максимальная яркости
исходного изображения равны 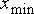 и и 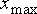 соответственно. Если эти параметры или один из них существенно отличаются от
граничных значений яркостного диапазона, то визуализированная картина выглядит
как ненасыщенная, неудобная, утомляющая при наблюдении.
соответственно. Если эти параметры или один из них существенно отличаются от
граничных значений яркостного диапазона, то визуализированная картина выглядит
как ненасыщенная, неудобная, утомляющая при наблюдении.
При линейном контрастировании используется линейное поэлементное
преобразование вида:
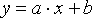
параметры которого  и и 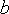 определяются желаемыми значениями минимальной
определяются желаемыми значениями минимальной 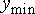 и максимальной и максимальной 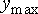 выходной яркости. С учетом этого,
представленное выражение может быть приведено к виду: выходной яркости. С учетом этого,
представленное выражение может быть приведено к виду:
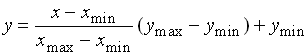
Функция линейного контрастирования представлена на рисунке:
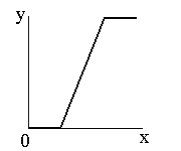
Рисунок 3. Функции препарирования типа линейное
контрастирование
void
LinearContrast(IplImage* img, IplLUT* lut)
{
//
Построение гистограммы для нахождения минимумов и
максимумов
iplComputeHisto(img,
plut);
// Определение минимальной
интенсивности
int
mn = 0;
while(!lut->value[mn])
mn++;
// Определение максимальной
интенсивности
int
mx = 255;
while(!lut->value[mx])
mx--;
// Подготовка lookup-таблицы к линейному
контрастированию
lut->interpolateType =
IPL_LUT_INTER; // режим
интерполяции
lut->num = 2; // количество ключевых
значений
lut->key[0] = 0; // нижнее
значение
lut->key[1] = 255; // верхнее
значение
lut->factor[0] = 255 / (mx - mn);
// наклон
lut->value[0]
= -lut->factor[0] * mn; // величина
сдвига
}
Пилообразное контрастирование
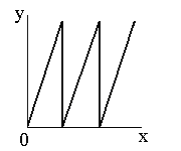
Рисунок 4. Функции препарирования типа пилообразное
контрастирование
void
NotchedContrast(IplLUT* lut)
{
// Подготовка
lookup-таблицы к пилообразному
контрастированию
lut->interpolateType =
IPL_LUT_INTER; // режим
интерполяции
lut->num = 4; // количество ключевых
значений
lut->key[0] = 0;
lut->key[1] = 85;
lut->key[2] = 170;
lut->key[3] = 255;
lut->factor[0] = 3; //
наклон
lut->factor[1] = 3; // наклон
lut->factor[2] = 3;
// наклон
lut->value[0]
= 0; // величина
сдвига
lut->value[1] = 0; // величина
сдвига
lut->value[2] = 0; // величина сдвига
}
| 
 Мой e-mail: iluhin@sktel.com.ua
Мой e-mail: iluhin@sktel.com.ua
 Мой e-mail: iluhin@sktel.com.ua
Мой e-mail: iluhin@sktel.com.ua