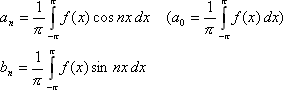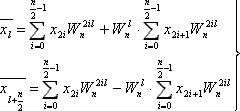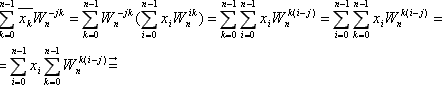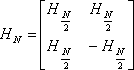Документный интерфейс.
Открытие изображения.uses JPEG;
var
JPEGImage: TJPEGImage;
Image: TImage;
begin
JPEGImage := TJPEGImage.Create;
JPEGImage.LoadFromFile (OpenDialog.FileName);
Image.Picture.Assign (JPEGImage);
JPEGImage.Free;
end;
Работа с изображением и его отображение.var
Bitmap: TBitmap;
Image: TImage;
begin
Bitmap := TBitmap.Create;
Bitmap.Assign (Image.Picture); //из Image – в Bitmap
…
Image.Picture.Assign (Bitmap); //из Bitmap – в Image
Bitmap.Free;
end;
Дополнительно может понадобиться создание
пустого изображения с необходимыми размерами и копирование в него
какой-либо части исходного. Это делается так: var
Bitmap: TBitmap;
BitmapArea: TRect;
Image: TImage;
begin
Bitmap := TBitmap.Create;
with BitmapArea do
begin
Left := 0;
Top := 0;
Right := Image.Width – 1;
Bottom := Image.Height – 1;
end;
with Bitmap do
begin
Height := Image.Height;
Width := Image.Width;
Canvas.CopyMode := CMSrcCopy;
Canvas.CopyRect (BitmapArea, Image.Canvas, BitmapArea);
end;
Image.Picture.Assign (Bitmap);
Bitmap.Free;
end;
Использование всяких линеек процесса (классы
TProgressBar или TGauge) – это, конечно, красиво, но может
существенно замедлить работу алгоритмов. Но вот использовать метод
Application.ProcessMessages в долгих цикличных процедурах было бы
не лишним, так как это создаёт «эффект независшего приложения»
(выполняется его периодическое обновление, а также обработка системных
событий). 
Работа с точками и цветами.var
B, G, R: Byte;
Image: TImage;
Pixel: TColor;
begin
Pixel := Image.Canvas.Pixels [0, 0];
R := Pixel and $000000FF; //или R := GetRValue (Pixel);
G := (Pixel and $0000FF00) shr 8; //или G := GetGValue (Pixel);
B := (Pixel and $00FF0000) shr 16; //или B := GetBValue (Pixel);
…
Pixel := B shl 8;
Pixel := (Pixel or G) shl 8;
Pixel := Pixel or R;
Image.Canvas.Pixels [0, 0] := Pixel;
end;
Однако за удобство приходится платить
временем: работа через массив Pixels[X,Y] требует огромных
ресурсов (из-за индексации по массиву), и на слабых машинах можно просто
недождаться результата. Поэтому есть замечательный метод
Bitmap.ScanLine, который возвращает указатель на целую строку
пикселей. Но элементы строки, на которую указывает ScanLine, –
это уже не 4-байтовый цвет, а реальные единицы информации,
соответствующие цветности картинки (для чёрно-белого изображения – 1
бит, для 4-цветного – 2 бита и т.д., для полноцветного – 3 или 4 байта).
Поэтому здесь могут возникнуть свои трудности, вызванные всё теми же
побитовыми операциями и выделением значений цветовых каналов в
малоцветных (от 256 цветов и меньше) изображениях. На этот случай
предлагается следующее: принудительно приводить цветность любой картинки
к 65 тысячам цветов (3-байтовый цвет, где каналы идут всё в той же
последовательности (B, G и R), по байту на канал),
и работать так: var
B, G, R: Byte;
Image: TImage;
P: PByteArray;
begin
Image.Picture.Bitmap.PixelFormat := PF24Bit;
P := Image.Picture.Bitmap.ScanLine [0];
X := 0;
repeat
R := P [X + 2];
G := P [X + 1];
B := P [X];
X := X + 3;
until X > 3 * Image.Width – 1;
end;
Яркость точки и гистограммы изображения.Y:=0.3*R+0.59*G+0.11*BГистограммой в данном случае называется так или иначе представленная (например, в виде столбчатой диаграммы) зависимость числа повторений того/иного значения яркости на всём изображении от этого самого значения (то есть сколько раз встречается абсолютно чёрная точка, абсолютно белая и др.); при этом можно рассматривать 4 гистограммы: по 3 каналам и по вычисленной яркости.
Изменения яркости и контрастности.Повышение/снижение яркости – это, соответственно, сложение/вычитание значения каждого канала с некоторым фиксированным значением (также в пределах от 0 до 255); при этом обязательно необходимо контролировать выход нового значения канала за пределы диапазона 0..255, например, так:
var
TempValue: Real;
Value: Byte;
begin
TempValue := Round (…);
if TempValue < 0
then Value := 0
else if TempValue > 255
then Value := 255
else Value := Round (TempValue);
end;
Повышение/снижение контрастности – это,
соответственно, умножение/деление значения каждого канала на некоторое
фиксированное значение (в том числе действительное), что приводит к
изменению соотношений между цветами и, соответственно, к более чётким
цветовым границам. На практике же существует такой принцип: изменение
контрастности не должно приводить к изменению средней яркости по
изображению, поэтому пользуются следующей формулой:
NewY:=K*(OldY-AveY)+AveY,где NewY – новое значение одного из каналов, K – коэффициент контрастности (K=(0..1) – снижение, K<1 – повышение контрастности), OldY – текущее значение того же канала, AveY – среднее значение того же канала по изображению (таким образом, алгоритм фактически является двухпроходовым). Обязательна всё та же коррекция нового значения при выходе его за границы 0..255.
Изменение цветности (бинаризация, оттенки серого,
негатив).Бинаризация – это преобразование изображения, в общем случае, к одноцветному (чаще всего к черно-белому). В терминах Photoshop это ещё называется «по уровню 50%», так как при этом выбирается некий порог (например, посередине), все значения ниже которого превращаются в цвет фона, а выше – в основной цвет. Само преобразование можно осуществлять по каналам, но в этом случае результирующее изображение не будет в прямом смысле бинарным (чёрно-белым), а будет содержать 8 чистых цветов, представляющих собой комбинации чистых красного, зелёного и голубого цветов, то есть будет бинарным по каналам. Поэтому лучше проводить преобразование над «полным» цветом точки, например, так:
var
Image: TImage;
MidColor, Pixel: TColor;
begin
MidColor := (High (TColor) – Low (TColor)) div 2;
Pixel := Image.Canvas.Pixels [0, 0];
if Pixel < MidColor
then Pixel := Low (TColor)
else Pixel := High (TColor);
Image.Canvas.Pixels [0, 0] := Pixel;
end;
Преобразование к оттенкам
серого заключается в получении яркости каждой точки по известной
формуле (Y:=0.3*R+0.59*G+0.11*B) и последующем копировании
полученного значения по все три канала (R=G=B:=Y).И, наконец, негатив получается простой заменой значения каждого канала на его дополнение до 255 (например, R:=255-R).
Наложение шума и фильтры шумоподавления.Зашумление можно выполнять любым способом, изменяющим каким-либо образом значения каких-то точек изображения. Например, так:
var
Image: TImage;
I, X, Y: Integer;
begin
for I := 1 to 100 do
begin
X := Random (Image.Width);
Y := Random (Image.Height);
Image.Canvas.Pixels [X, Y] := ClBlack; //случайные точки становятся чёрными
end;
end;
Для начала введём один специальный термин:
апертура фильтра – это размер окна (части изображения), с которым
фильтр работает непосредственно в данный момент времени; окно это
постепенно передвигается по изображению слева направо и сверху вниз на
один пиксель (то есть на следующем шаге фильтр работает с окном,
состоящим не только из элементов исходного изображения, но и из
элементов, ранее подвергнувшихся преобразованию, – своего рода
«принцип снежного кома»). Кроме того, заметим, что если речь идёт
об окне, представляющем собой строку элементов изображения ([X][X][X]),
то такое преобразование называется одномерным; соответственно,
существует и двумерное преобразование.Сглаживающий фильтр основывается на следующем принципе: находится среднее арифметическое значение всех элементов рабочего окна изображения (отдельно по каждому из каналов), после чего это среднее значение становится значением среднего элемента (речь идёт о нечётной апертуре фильтра; для двумерного случая средним элементом будет средний элемент по горизонтали и вертикали, то есть центр квадрата). Выглядит это примерно так:
var
Image: TImage;
X, Y: Integer;
begin
for X := 1 to Image.Width – 2 do
for Y := 1 to Image.Height – 2 do with Image.Canvas do
Pixels [X, Y] := (
Pixels [X – 1, Y – 1] + Pixels [X – 1, Y] + Pixels [X – 1, Y + 1] +
Pixels [X, Y – 1] + Pixels [X, Y] + Pixels [X, Y + 1]+
Pixels [X + 1, Y – 1] + Pixels [X + 1, Y] + Pixels [X + 1, Y + 1]) div 9;
end;
Внимание! Под действие
фильтра могут не попадать крайние элементы изображения (так получается в
приведённом примере), поэтому при искусственном зашумлении их лучше
преднамеренно не зашумлять, либо обрабатывать каким-то образом частный
случай крайних точек (например, для угла изображения при апертуре 3
суммировать не 9 точек, а 4, и результат отправлять в этот самый
угол).Медианный фильтр основывается на нахождении медианы – среднего элемента (но не среднего арифметического) последовательности в результате её упорядочения по возрастанию/убыванию и присваиванию найденного значения только среднему элементу (речь снова о нечётной апертуре). Например, для той же апертуры 3 и двумерного фильтра (как в примере выше) мы должны упорядочить 9 точек (например, по возрастанию), после чего значение 5й точки упорядоченной последовательности отправить в центр окна фильтра (3х3). Для упорядочения можно использовать любой из известных методов сортировки, например, быструю сортировку Хоара:
procedure SortBytes (var Bytes: array of Byte; Left, Right: Integer);
var
I, J: Integer;
W, X: Byte;
begin
I := Left;
J := Right;
X := Bytes [(Left + Right) div 2];
repeat
while Bytes [I] < X do I := I + 1;
while X < Bytes [J] do J := J – 1;
if I lt;= J then
begin
W := Bytes [I];
Bytes [I] := Bytes [J];
Bytes [J] := W;
I := I + 1;
J := J – 1;
end;
until I > J;
if Left < J
then SortBytes (Bytes, Left, J);
if I < Right
then SortBytes (Bytes, I, Right);
end;
Для фиксированной малой апертуры можно
использовать какой-либо вырожденный (частный) вариант сортировки,
построенный на операторах условия. 
Методы выделения границ.Внимание! Все методы выделения границ работают с яркостью точки, то есть со значением, полученным из значений трёх цветовых каналов по известной формуле (см. выше). Однако для этого вовсе необязательно предварительно преобразовывать всё изображение к оттенкам серого, достаточно лишь получать значение яркости в тот момент и для той точки, с которой идёт работа, а полученное в результате преобразований значение повторять по трём каналам. И ещё: нельзя забывать о необходимости коррекции результата (0..255).
Метод Кирша работает с двумерной апертурой 3х3 следующего вида:
|
Si = Ai +
Ai(+)1 + Ai(+)2 Ti = Ai(+)3 + Ai(+)4 + Ai(+)5 + Ai(+)6 + Ai(+)7 |
function AddMod8 (X, Y: Integer): Integer;
var Sum: Integer;
begin
Sum := X + Y;
if Sum > 7 then Sum := Sum – 8;
Result := Sum;
end;
После находятся значения модуля разности |
5*Si – 3*Ti | для каждого i от 0 до 7 и
значение максимума среди этих модулей:Возможно, для обеспечения наблюдаемости потребуется повышение порога яркости сложением эдак с числом 100. Окончательное значение F' заносится в элемент F, после чего рабочее окно сдвигается на один элемент влево (далее – слева направо и сверху вниз).
Метод Лапласа осуществляет домножение каждого элемента двумерной апертуры 3х3 на соответствующий элемент так называемой матрицы Лапласа:
|
|
|
= |
|
После перемножения все полученные значения элементов суммируются, при необходимости повышается порог яркости сложением эдак с числом 100, и результат помещается в центр, то есть в точку E. Затем рабочее окно сдвигается на один элемент влево (далее – слева направо и сверху вниз).
Существуют и другие матрицы Лапласа:
|
, |
|
, |
|
, |
|
и так далее… |
Метод Робертса, как показывает практика, является самым простым, самым быстрым и эффективным (поистине, всё гениальное – просто). Работает он с двумерной апертурой 2х2 следующего вида:
|
 |
Метод Собела работает с двумерной апертурой 3х3 следующего вида:
|
X = ( A3 + 2 * A4 +
A5 ) – ( A1 + 2 * A8 +
A7 ) Y = ( A1 + 2 * A2 + A3 ) – ( A7 + 2 * A6 + A5 ) |
Возможно, для обеспечения наблюдаемости потребуется повышение порога яркости сложением эдак с числом 100. Окончательное значение F' помещается вместо элемента F, после чего рабочее окно сдвигается на один элемент влево (далее – слева направо и сверху вниз).
Метод Уоллеса работает с двумерной апертурой 3х3 следующего вида:
|
 |
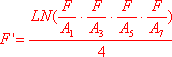Статистический метод является двухпроходовым и применим для любой апертуры, даже для прямоугольной. На первом этапе вычисляется среднее значение яркости по текущему рабочему окну:
Далее вычисляется значение среднеквадратичного отклонения значений элементов рабочего окна от среднеарифметического значения:
Затем значения всех элементов рабочего окна домножаются на полученное отклонение:
Возможно, для обеспечения наблюдаемости потребуется повышение порога яркости сложением эдак с числом 100.
Внимание! Статистический метод – единственный из здесь рассмотренных, у которого изменяются значения сразу всех элементов.
Распознавание текста.Шумоподавление. Это удаление возможного зашумления изображения, являющегося следствием неидеальности устройства, породившего изображение (например, сканера). В данном случае шумоподавление выполняется одним из лучших фильтров – двумерным медианным. Этап необязательный.
Бинаризация. Это преобразование изображения, в результате которого значение каждого его элемента становится равным 0 или 1, то есть бинарным; в общем случае преобразование осуществляется отдельно по каждому каналу, в данном же случае – над общим значением яркости изображения, то есть результирующее изображение будет полностью чёрно-белым. Этап необязательный.
Выделение строк. Оно необходимо для
последующего выделения символов и их распознавания и осуществляется
посредством выполнения вертикальной проекции (построения гистограммы)
строк пикселей, на которой находятся области резкого перепада числа
значимых (чёрных) пикселей в строке; если число чёрных точек в
предыдущей строке пикселей было значительно меньше их числа в текущей
строке, то это говорит о начале строки текста, и наоборот. Основная
проблема здесь – в выборе порога (понятия «значительно» больше/меньше),
так как изображение может быть зашумлено. Кроме того, если отдельные
верхние/нижние элементы символов на соседних строках заходят друг за
друга, то такие строки могут быть неразделимы.
Выделение символов. Оно выполняется после
выделения строк и необходимо для последующего распознавания символов.
Процесс аналогичен выделению строк: выполняется горизонтальная проекция
(построение гистограммы) столбцов пикселей, на которой находятся области
резкого перепада числа значимых (чёрных) пикселей в строке; если число
чёрных точек в предыдущем столбце пикселей было значительно меньше их
числа в текущем столбце, то это говорит о начале символа, и наоборот.
При этом может использоваться тот же порог выделения, что и для строк.
Кроме того, после выделения символа по горизонтали осуществляется также
его выделение по вертикали (уточнение границ), так как его границы могут
отличаться от границ всей строки. Проблема неразделимости пересекающихся
в проекции символом сохраняется.Выбор шрифта. Выбранный шрифт определяет эталоны символов, с которыми будут сравниваться распознаваемые области изображения. В более общей задаче распознавания шрифт должен определяться автоматически, то есть в библиотеке эталонов должны находиться символы всех шрифтов, и по максимальному совпадению определяется шрифт. В нашем случае ограничимся типом шрифта, выбираемым пользователем. На этом этапе алфавит, представленный в виде идеального изображения (сгенерированного или загруженного), также проходит этапы выделения строк и столбцов, но с учётом того, что последовательность символов на эталонном изображении известна, и выделенным областям изображения можно сразу поставить в соответствие конкретные символы алфавита.
Распознавание. Непосредственное распознавание – это сравнение выделенных областей изображения с имеющимися эталонами символов и проверка результата на допустимость. Сравнение можно выполнять любым из известных методов, например, методом маски (самый простой, но наглядный), заключающемся в сложении распознаваемого и эталонного изображений по модулю 2 и определении числа нулей в результирующем изображении. При этом отметим следующие моменты:
- описание символов распознаваемого текста после их выделения представляет собой координаты их углов на распознаваемом изображении; библиотека эталонов – то же, но для эталонного изображения всего алфавита и с указанием собственно кода соответствующего символа алфавита;
- в процессе распознавания осуществляется перебор во внешнем цикле всех выделенных символов распознаваемого текста и перебор во внутреннем цикле всех эталонов, то есть каждому символу распознаваемого текста поочерёдно ставятся в соответствие все эталонные символы, и определяется степень их совпадения;
- для повышения эффективности распознавания вводятся такие параметры как допустимое отклонение разметов символов от эталонов (чтобы не пытаться сравнивать символ «,» с эталоном «Ж») и минимальная степень совпадения символов с эталонами (если для текущего сравнения она меньше, то символ не распознан);
- символ считается распознанным, если есть хотя бы один эталон, степень совпадения с которым оказалась не меньше минимально допустимой; при этом если таких эталонов несколько, то выбирается тот, с которым была достигнута наибольшая степень совпадения; при этом если эталонов с одинаковой наибольшей степенью совпадения несколько, выбирается первый по перечню алфавита.
Для хранения описаний изображений символов можно использовать невизуальный объект TStringList, позволяющий легко работать со списком значений произвольной длины. Принятый формат хранения значений координат при этом может выглядеть так:
StringList [I] := IntToStr (Top) + ',' + IntToStr (Bottom) + ',' +
IntToStr (Left) + ',' + IntToStr (Right);
То есть каждая строка списка – это координаты
верхней, нижней, левой и правой границы изображения символа, разделённые
запятой. После выделения символов из списка удаляются описания ранее
выделенных строк.Из алфавита эталонов были преднамеренно удалены все символы, порождающие ситуацию неоднозначного распознавания (например, «Й» или «Ы»). Эталонное изображение генерируется автоматически с использованием выбранного шрифта.
Для получения результирующего изображения как сложения по модулю 2 используется режим TCanvas.CopyMode:=CMSrcInvert; и метод TCanvas.CopyRect(CurrentRect, AlphabetBitmap.Canvas, StandardRect). Степень соответствия определяется по формуле:
CharFill := BlackPixels / (ScannedHeight * ScannedWidth);
где CharFill – заполненность
результата сравнения нулями, BlackPixels – число чёрных (нулевых)
пикселей на совмещённом изображении таким же размером, что и
распознаваемое изображение (ScannedHeight x ScannedWidth).
Непрерывное преобразование Фурье.
где a0, an, bn (n є N) – коэффициенты ряда, называется рядом Фурье, или тригонометрическим рядом; возможно искусственное усложнение записи ряда с целью упрощения инженерных расчётов. Ряд Фурье используется для разложения непрерывных функций с целью дискретизации.
Известны формулы Эйлера – Фурье для вычисления коэффициентов ряда Фурье:
Эти формулы имеют место, если тригонометрический ряд для всех значений x сходится к функции f(x) (предполагается, что эта функция периодическая, с периодом 2Пи), и для этой функции существует интеграл
Функция f(x) может быть разрывной; при этом указанный интеграл становится несобственным. Непериодические функции, определённые в промежутке (-Пи; Пи) тоже можно разлагать в ряд Фурье, но со следующей оговоркой: за пределами указанного промежутка и на его концах ряд Фурье может иметь сумму, отличную от соответствующего значения самой функции.
Теорема. Пусть функция непрерывна на промежутке (-Пи; Пи) и либо не имеет здесь разрывов, либо имеет их конечное число. Тогда для этой функции ряд Фурье сходится всюду; сумма его равна значению функции f(x) для всякого значения x є (-Пи; Пи), на обоих же концах промежутка сумма ряда равна [f(-Пи)+f(Пи)]/2.
Интегралы
для чётной функции равны между собой, а для нечётной – разнятся знаками, поэтому имеем:
соответственно.
Ряд Фурье для чётной функции не содержит синусов, а его коэффициенты равны:
для нечётной функции – не содержит косинусов и имеет коэффициенты:
Очевидно, что для работы с произвольными функциями необходимо реализовать универсальную функцию численного интегрирования.
Непрерывное преобразование Фурье выполняется над фиксированным сигналом, не зависящим от загруженного в программу изображения. Этот сигнал описывается функцией вида:
function Signal (X: Real): Real;
begin
if Abs (X) > 1
then X := X – 2 * Round (X / 2);
if X < – 0.4
then Result := 0.25;
if (X >= – 0.4) and (X < 0.4)
then Result := 0.5;
if (X >= 0.4) and (X < 0.8)
then Result := 0.75;
if X >= 0.8
then Result := 0.25;
end;
Его интегрирование можно осуществлять
численным методом трапеций: function Integral (F: TFunction; A, B, H: Real): Real;
var Square, X: Real;
begin
Square := 0;
X := A;
while X < B – H do
begin
Square := Square + 0.5 * (F (X) + F (X + H)) * H;
X := X + H;
end;
Result := Square;
end;
Дискретное преобразование Фурье.где k=(0,n-1), W=e-j*Пи/n, где j – мнимая единица.
Существуют такие Wik, у которых (ik) равны. Нетрудно заметить, что для выполнения n-точечного преобразования Фурье необходимо выполнить n(n-1) комплексных сложений и (n-1)(n-1) комплексных умножений (с учётом W0=1). При этом множитель Wik будет использован столько раз, сколько делителей из диапазона (0,n-1) у показателя степени (ik).
Имеем:
Поскольку sin Альфа = – sin (Альфа+Пи), cos Альфа = – cos (Альфа+Пи), то
откуда следует, что
(1)
Таким образом, диапазон степеней (ik) с помощью формулы (1) мы сокращаем с
(2)
Пусть n – длина исходной последовательности чисел {x0, x1, …, xn-1} чётна, тогда преобразование Фурье для такой последовательности можно записать в виде:
С учётом формулы (1), а также выражения
(3)
формулу (3) часто записывают в виде:
Рассмотрим первую сумму формулы (3). Положив n / 2 = m, получим:
(4)
1) n=2m;
2);
3)Аналогичные рассуждения можно провести и в отношении второй суммы формулы (3). Таким образом, ДПФ исходной последовательности размерностью n=2m свелось к двум ДПФ последовательностей размерностью m чисел каждая, составленных из чётных и нечётных элементов исходной последовательности..
Формулы (3) и (4) являются основой для построения алгоритма быстрого преобразования Фурье (БПФ). Этот алгоритм за счёт рекурсивного применения формулы (3) сводит ДПФ исходной последовательности размерности n=2l, где l є N, к набору 2-точечных преобразований Фурье.
По определению имеем:
Умножим x-k на Wn-jk и просуммируем по k=0..(n-1):
Можно доказать, что
где a є Z, a>0, поэтому
имеем:
– мы получили формулу для обратного ДПФ (ОДПФ):
откуда видно, что ОДПФ есть прямое ДПФ (ПДПФ) результата предыдущего ПДПФ, делённое на n.
Двумерное ДПФ – это ДПФ над матрицей:
где k,i=(0,n-1), l,j=(0,m-1), то есть это есть последовательное одномерное ДПФ сначала над строками, а потом над строками.
Общий вид обратного двумерного ДПФ:
При практической реализации в качестве исходных данных для демонстрации работы алгоритмов ДПФ удобно использовать значения точек изображения, подвергающегося обработке другими алгоритмами. При этом под «значениями» точек понимается либо значения каждого из цветовых каналов, либо значение яркости (найденное по известной формуле), либо значение типа TColor элемента массива Pixels[], – это неважно. Важно то, что всё выполняется примерно по следующий схеме:
- Значения точек заносятся в область памяти, выделенную для действительных частей дискретов (речь ведь идёт о работе с комплексными числами).
- Область памяти, выделенная для мнимых частей дискретов, заполняется нулями (так как значения точек изображения – чисто действительные числа).
- Вызывается процедура необходимого преобразования Фурье (одномерное или двумерное БПФ), которой передаются указатели на выделенные области памяти и их размеры, а также направление преобразования (в данном случае прямое).
- В качестве наглядного представления коэффициентов, полученных после преобразования (в тех же областях памяти) используются модули комплексных чисел, которые делаются значениями соответствующих точек изображения.
- Сами области памяти сохраняются до выполнения обратного преобразования, так как они хранят комплексные значения коэффициентов (после прямого БПФ мнимые части отличны от нуля).
- При выполнении обратного преобразования той же универсальной процедуре передаются указатели на хранимые области памяти, их размеры и направление преобразования (обратное).
- Модули комплексных чисел, полученных после обратного БПФ, являются исходными значениями точек изображения, так как их мнимые части равны нулю.
- Освобождаются выделенные области памяти.
Пример процедуры для выполнения одномерного БПФ приведён ниже:
//© 1999 Головинов И.А.
procedure LinearFDFT (Re, Im: PReal; Count: Word; Direct: ShortInt);
var
I: Word;
K: Real;
PIm, PRe: PReal;
procedure LFDFT (SrcRe, SrcIm: PReal; Cnt: Word);
var
EvenRe, OddRe, PEvenRe, POddRe, PRe, PSrcRe: PReal; …; //то же – для мнимых
Factor: Real;
HalfCnt, I, Size: Word;
HEvenIm, HEvenRe, HOddIm, HOddRe: THandle;
X, Y, WIm, WRe: Real;
begin
PSrcRe := SrcRe; …;
if Cnt = 2 then
begin //тривиальная операция «бабочка»
Inc (PSrcRe); …;
X := SrcRe^; Y := PSrcRe^;
SrcRe^ := X + Y; PSrcRe^ := X – Y;
X := SrcIm^; Y := PSrcIm^;
SrcIm^ := X + Y; PSrcIm^ := X – Y;
end else
begin //переупорядочение и рекурсивный вызов для полпоследовательностей
Factor := K / Cnt;
HalfCnt := Cnt div 2;
Size := HalfCnt * SizeOfReal + 1;
HEvenRe := GlobalAlloc (GMem_Fixed, Size); …;
HOddRe := GlobalAlloc (GMem_Fixed, Size); …;
EvenRe := GlobalLock (HEvenRe); …;
OddRe := GlobalLock (HOddRe); …;
PEvenRe := EvenRe; …;
POddRe := OddRe; …;
//Разбивка на (не)чётные подпоследовательности
for I := 0 to Cnt – 1 do
begin
if Odd (I) then
begin
POddRe^ := PSrcRe^; …;
Inc (POddRe); …;
end else
begin
PEvenRe^ := PSrcRe^; …;
Inc (PEvenRe); …;
end;
Inc (PSrcRe); …;
end;
//Рекурсивная обработка (не)чётных подпоследовательностей
LFDFT (EvenRe, EvenIm, HalfCnt);
LFDFT (OddRe, OddIm, HalfCnt);
//Сборка обработанных подпоследовательностей
PSrcRe := SrcRe; …;
PRe := SrcRe; …;
Inc (pRe, HalfCnt); …;
PEvenRe := EvenRe; …;
POddRe := OddRe; …;
for I := 0 to HalfCnt – 1 do
begin
WRe := Cos (Factor * I); WIm := – Sin (Factor * I);
PSrcRe^ := POddRe^ * WRe – POddIm^ * WIm;
PSrcIm^ := POddRe^ * WIm + POddIm^ * WRe;
PRe^ := pSrcRe^; …;
PSrcRe^ := pEvenRe^ + PSrcRe^; …;
PRe^ := PEvenRe^ – PRe^; …;
Inc (PSrcRe); …;
Inc (PRe); …;
Inc (PEvenRe); …;
Inc (POddRe); …;
end;
GlobalUnlock (HEvenRe); …;
GlobalUnlock (HOddRe); …;
GlobalFree (HEvenRe); …;
GlobalFree (HOddRe); …;
end;
end;
begin
K := 2 * Pi * Direct;
LFDFT (Re, Im, Count);
if Direct < 0 then
begin //Дополнительное деление на n для обратного преобразования
PRe := Re; …;
for I := 1 to Count do
begin
PRe^ := PRe^ / Count; …;
Inc (PRe); …;
end;
end;
end;
Оптимизация здесь может заключаться в
использовании другого типа данных (константа SizeOfReal может
быть заменена на выхов оператора SizeOf(Type) для конкретного
типа Type), других способов выделения и освобождения памяти
(например, с использованием функций GetMem и FreeMem) и
т.п. В случае двумерного преобразования используется та же функция, но
последовательно, сначала для строк, потом для столбцов (или наоборот).
Преобразование Уолша-Адамара.где
– безразмерное время (
), k є N – порядок (номер) функции,Система функций Радемахера ортонормированна на интервале (0,1), то есть
однако неполна.
Функции Уолша, образующие полную ортонормированную систему, теперь можно определить так:
где «(+)» – сложение по модулю 2; w – порядок (номер) функции; n=log2 N, где N=2n – количество функций системы; wi – i-тый разряд двоичного представления порядка функции w (отсчёт слева, начиная с 0).
(5)
Функции Уолша могут служить базисом для спектрального представления сигнала, то есть любую интегрируемую на интервале
функцию можно представить рядом по системе
функций Уолша:с коэффициентами
Способ нумерации функций в системе называется упорядочением. Функции Уолша, сформированные в соответствии с выражением (5), упорядочены по Уолшу. На практике также применяется упорядочение по Адамару (had(h,Эта)) и по Пэли (pal(p,Эта)).
Функции had(h,Эта) можно сформировать с помощью матрицы Адамара. Матрицей Адамара HN порядка N=2n, n є N называется квадратная матрица размера N x N с элементами +1 такая, что
HN x HNT = N x E,где HNT – транспонированная матрица, E – единичная матрица; при этом H1=1.
Матрицу Адамара легко построить рекурсивно, так как:
Функция Уолша, упорядоченная по Адамару (had(h,Эта)) с номером h, является последовательностью прямоугольных импульсов длительностью 1/N от интервала (0,1) с единичными амплитудами и полярностями, соответствующими знакам элементов h-той строки матрицы Адамара.
Для цифрового анализа сигнала используются дискретные функции Уолша, которые являются отсчётами соответствующих непрерывных функций. Каждый отсчёт расположен в середине связанного с ним элемента непрерывной функции длительностью 1/N от интервала (0,1). Дискретные функции Уолша, упорядоченные по Уолшу, можно определить так:
где xk – k-тый разряд в представлении номера отсчёта x в двоичной системе счисления:
Другой формой представления дискретных функций Уолша является матрица Адамара, номера столбцов которой соответствуют номерам дискретных значений (отсчётов) функций Уолша, а номера строк – номерам функций Уолша.
Дискретное преобразование Уолша (ДПУ) определяется так:
что в матричном виде (дискретное преобразование Уолша – Адамара, ДПУ) выглядит так:
Соответственно, обратное ДПУ:
так как
где
– обратная матрица Адамара, а
Hn*Hn-1=E – единичная матрица,
при домножении на которую никакая матрица не изменяется.Схема быстрого преобразования Уолша – Адамара (БПУ) полностью аналогична схеме БПФ. Отличие в следующем:
- поскольку базисные функции являются последовательностями прямоугольных импульсов единичной амплитуды, то коэффициенты в разложении будут +/-1, то есть вместо множителя W будет только сложение/вычитание;
- упорядочение элементов выходного вектора зависит (определяется) упорядочением системы функций Уолша (по Уолшу, по Адамару).
Двумерное БПУ определяется так:
где X – матрица N x N, где N=2n, n є N. Соответственно, обратное двумерное БПУ:
На практике БПУ строится на основе ранее написанных процедур БПФ, в которых удаляется работа с мнимыми частями, переупорядочение перед рекурсивным вызовом и домножение на W при сборке.
