|
Источник: Банковские технологии. - 2001. - №12. - с.70-77 ФИНАНСОВЫЕ ВРЕМЕННЫЕ РЯДЫ: КУСОЧНОЕ ПРОГНОЗИРОВАНИЕ И ПРОБЛЕМА ОБНАРУЖЕНИЯ ПРЕДВЕСТНИКОВ СУЩЕСТВУЮЩЕГО ИЗМЕНЕНИЯ ЗАКОНОМЕРНОСТИ Александр Батуро, Наталья Еременко Основная проблема в задаче анализа и прогнозирования заключается в построение модели, адекватно отражающей динамику финансовых временных рядов. Рыночный механизм, характеризующийся огромным количеством постоянно меняющихся связей, зависит от множества внешних факторов, способных существенно повлиять на всю структуру его зависимостей, причем воздействие может быть самым разнообразным. Появление тех или иных внешних факторов, как правило, никак не отражается в предыстории финансового временного ряда, но вызывает значительное нарушение его динамики. Именно в этом состоит особенность практически всех финансовых временных рядов. Принятие нового закона, изменение ставки рефинансирования, отставка правительства, смена руководства одной из крупнейших российских компаний, предвыборная кампания, громкие скандалы — вот список немногих факторов, способных существенно повлиять на финансовый рынок. Другая проблема, с которой приходится сталкиваться при моделировании финансовых временных рядов, состоит в том, что финансовые рынки постоянно испытывают потрясения, примерами которых являются обвал рынков Юго-Восточной Азии, финансовый кризис в России. Это особенно актуально для российского рынка, поскольку риск мгновенно потерять вложенные инвестором средства остается достаточно высоким. Трудно найти объективную причину того, что данное событие произошло именно тогда, когда произошло, а не месяцем раньше или позже. Возникает проблема обнаружения факторов, являющихся предвестниками критических явлений, меняющим направление движения тренда и способных привести в том числе и к кризису. Для решении задачи анализа и прогнозирования финансовых временных рядов применяется два основных подхода: теоретический и практический. Теоретический подход объединяет модели, гипотезы, теории, дающие представление о наиболее общих зависимостях рыночного механизма, представленных в некотором идеализированном виде. Практический подход уделяет больше внимания непосредственному моделированию финансовых временных рядов, которые рассматривает как реализацию некоторой сложной зависимости неизвестного вида. Главное в данном подходе то, что используемая модель должна успешно решать задачу прогнозирования, а вид ее не имеет значения. Хотя, с другой стороны, для лучшего понимания зависимостей желательно, чтобы способ вычисления будущих значений финансового временного ряда имел осмысленное толкование. Выбор модели, как правило, осуществляется эмпирическим методом на основе некоторого заданного универсального семейства предикторов, возможности которого позволяют описать любой временной ряд. Выбор того или иного семейства моделей отражает специфику решения задачи прогнозирования. Наиболее ярким представителем практического подхода является технический анализ. Кроме того, в последнее время получили широкое распространение регрессионные методы, а также методы, основанные на Wavelet- преобразовании и на нейронных сетях. Общая черта, объединяющая оба подхода, заключается в попытке построения единой модели для финансового временного ряда. Однако из сказанного выше следует, что построение такой модели наталкивается на ряд принципиальных трудностей, обусловленных природой финансового временного ряда. Идея подхода, основанного на кусочном моделировании временного ряда состоит в следующем. Исследования показывают, что один и тот же предиктор (Предиктор №1) с разной точностью моделирует разные участки временного ряда. В то время как существует другой предиктор (Предиктор №2), который на одних участках временного ряда предсказывает лучше, чем Предиктор №1, а на других — хуже (или также). Так можно задать целый набор предикторов, которые будут иметь свои особенности. Для прогнозирования выбирается тот предиктор, который лучше остальных спрогнозировал некоторый участок временного ряда. (Чаще всего он состоит из последних нескольких значений этого ряда.) При правильной настройке такой системы можно добиться лучшего качества прогнозирования по сравнению с каждым предиктором из заданного набора в отдельности. Иллюстрация предлагаемого подхода представлена на рисунке: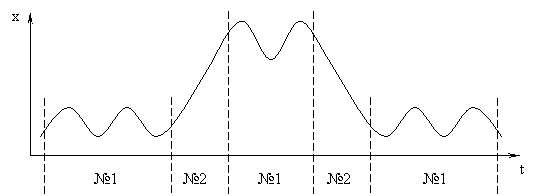 
Рисунок 1. Кусочное моделирование временного ряда
Общий вид предиктора №1 имеет вид a1*sin(a2*t+a3)+a4, где a1,...,a4 — настроечные коэффициенты, которые для каждого отдельного участка временного ряда рассчитываются отдельно. Общий вид предиктора №2 имеет вид a1*t+a2, где a1, a2 — коэффициенты, настраиваемые по аналогичной схеме. Цифрами «№1» и «№2» обозначены участки временного ряда, на котором предиктор с соответствующим номером имеет лучшие прогнозирующие свойства. Две основные проблемы которые необходимо решить при кусочном моделировании заключаются в определении набора предикторов и правила выбора одного из них для прогнозирования некоторого участка временного ряда. Обычно эти проблемы для реальных временных рядов решаются эмпирически, но можно предложить некоторые приемы. Фундаментальное предположение о временном ряде Наблюдаются величины X =X(t), X(t)=(х1(t), x2(t),…,xp(t)), p>=1 в дискретные моменты времени t1...tk. (Обычно рассматривается ситуация когда наблюдения производятся через равные промежутки времени В этом случае можно записать t1= t0+1dt, t2=t0+2dt, …, tk=t0+kdt и т.д., где t0 — некоторый начальный момент времени, dt минимальный промежуток времени между наблюдениями). Задача прогнозирования временного ряда заключается в том чтобы по его известному участку
Прежде чем перейти к непосредственному решению данной задачи, необходимо сформулировать ряд фундаментальных предположений о природе временного ряда, в рамках которых можно будет применять ту или иную схему прогнозирования: |
Предикторы и их настройка Ключевым в задаче прогнозирования является понятие «адаптивный предиктор». Предиктором F называется любая вычислительная схема, которая позволяет по значениям одних параметров (входных) получать значения других (выходных) В качестве выходных задаются те параметры, значения которых нужно спрогнозировать, т.е. будущие значения временного ряда. Если, кроме входных параметров, для расчета также используются настроечные коэффициенты, то такой предиктор называют адаптивным. Его обычно применяют тогда, когда имеется некоторый поток данных, к которому нужно постоянно адаптировать работу предиктора. Один из способов, чтобы сделать это, заключается в изменении значении набора настроечных коэффициентов, производимом с помощью некоторой процедуры настройки. Набор входных и выходных параметров определяет тип предиктора. Если в качестве входных параметров используются значения предыстории временного ряда, то предиктор называется авторегрессионным, например, предиктор По определенным признакам все адаптивные предикторы можно объединить в семейства и классы. Семейства адаптивных предикторов, которые могут быть использованы для решения задачи предсказания временного ряда - это линейные тренды, квадратичные тренды, тренды k-го порядка, чиненные авторегрессионные предикторы, квадратичные авторегрессионые предикторы, авторегрессионые предикторы k-го порядка, нейронные сети и другие адаптивные предикторы. На предиктор могут накладываться ограничения например ограничения в виде набора неравенств на значения настроечных коэффициентов предиктора, ограничения на применение процедуры настройки предиктора. Для прогнозирования будущих значении временного ряда используется процедура прогнозирования. Разность времени между моментами начала прогнозирования и его концом называют глубиной прогноза. Глубину, при которой прогноз производится с заданной точностью, называют горизонтом прогнозирования. Наиболее просто процедура прогнозирования выглядит для трендовых предикторов - в качестве аргумента предиктора нужно указать момент времени, на который требуется получить прогноз. Например, для момента времени t+1 прогноз вычисляется следующим образом При решении задачи прогнозирования временного ряда адаптивным предиктором активно применяется процедура настройки или обучения. Смысл се заключается в подборе таких значений настроечных коэффициентов предиктора, которые позволили бы оптимизировать его свойства (в смысле некоторого заданного критерия). Эта процедура зачастую используется для настройки предиктора на заданную выборку - таблицу, в которой одна часть столбцов описывает значения входных параметров, а другая — значения выходных параметров. Строку такой таблицы называют примером, который будем обозначать парой (уk хk)<.i> где k - номер примера в выборке (1< k Рассмотрим некоторый адаптивный предиктор:
|
|
|
В процессе настройки требуется оценить работу предиктора на всей выборке. Для этого на основе отдельных оценок Н(уk) формируется оценка всей выборки. Для этого может применяться простое суммирование.
Решением оптимизационной задачи будет набор настроечных коэффициентов Прогнозирование и «разладки» Общая схема кусочного прогнозирования временного ряда содержит два этапа, подготовительный и основной. На первом этапе происходит сбор информации о предсказывающих свойствах каждой из предикторных схем, а на втором — прогнозирование участка временного ряда предикторной схемой, которая показала лучшие предсказывающие свойства Подготовительный и основной этапы представлены на рисунке 1.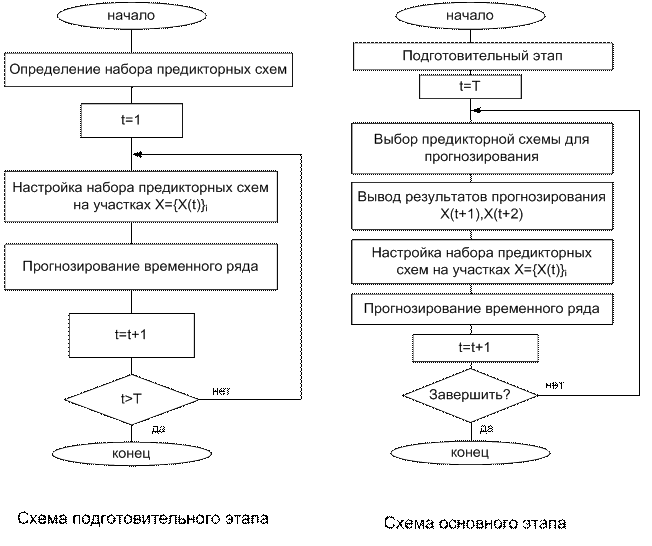 
Рисунок 2. Блок-схема метода кусочного прогнозирования Для определения предикторной схемы с лучшими предсказывающими свойствами используется правило выбора. Это правило на основе реальных и прогнозных значений временного ряда оценивает работу (согласно некоторому критерию Н) каждой предикторной схемы из набора Ф, а затем выбирает лучшую из них. Предикторную схему, выбранную с помощью данного правила, будем называть ведущей. Мы 6удем пользоваться следующим правилом: для прогнозирования временного ряда в момент времени t будет применяться предикторная схема с минимальным значением критерия Н на данный момент; если таких схем несколько, то выбирается любая из них. Формально запишем это таким образом: Если выбрана некоторая предикторная схема, то она остается ведущей до тех пор, пока выдаваемый ею прогноз удовлетворяет заданному пользователем критерию. Если ошибка предсказания временного ряда начинает существенно возрастать, то это означает, что данная предикторная схема непригодна для дальнейшего прогнозирования В этом случае будем говорить о разладке — ситуации, когда ведущая предикторная схема не удовлетворяет некоторому заданному критерию качества. Предлагаемый подход может быть применен для решения проблемы обнаружения предвестников существенных изменений закономерности во временном ряде Это имеет большое значение для финансового рынка. Если некоторый предиктор с заданной точностью предсказывает достаточно длинный участок финансового временного ряда, то с высокой степенью уверенности можно говорить о том, что используемый предиктор на данном участке достаточно точно описывает динамику этого ряда. Если после некоторого шага ошибка предсказания начинает существенно возрастать, то будем говорить о нарушении закономерности, зафиксированной в данном предикторе, и появлении разладки. Разладка может свидетельствовать о нарушении закономерности в динамике этого ряда — все это может служить предвестником критических явлений для финансового рынка. Из-за неодинаковой информированности участников рынка реакция на некоторое событие, способное существенно изменить динамику рынка, происходит не сразу и имеет лавинообразный характер. Система, основанная на кусочном моделировании, может реагировать раньше значительной части трейдеров, поскольку тоньше отслеживает изменения зависимостей финансовых временных рядов Предлагаемый метод был апробирован для обнаружения предвестников критических явлений в финансовом временном ряде. Об авторах Еременко Наталья Макаровна - заместитель директора Красноярского филиала Банка Москвы. |
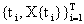оценить будущие значения величины X.
, где параметр d определяет глубину предыстории (кочичество этементов временного ряда, используемых для предсказания его будущего значения). Если в качестве аргумента предиктора используется параметр времени t то предиктор называется трендовым, например, 
. Это — наиболее распространенные типы предикторов.
.
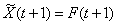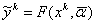. Настройка этого предиктора F на за данную выборку производится путем подбора настроечных коэффициентов 
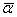, при этом для определения качества работы предиктора на обучающей выборке будем использовать функцию оценки Н., или просто оценку. В этом случае задача поиска оптимального набора настроечных коэффициентов сводится к оптимизационной задаче минимизации функции оценки Н на обучающей выборке. Перечислим некоторые виды оценок которые могут быть применены для настройки предикторов:
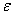, где 
, зависящими от номера выходного сигнала;
из множества допустимых значений А, обеспечивающих глобальный минимум функции 
.
Затем обученный предиктор проверяется на тестовой выборке и делается вывод о качестве предсказания. Качество прогноза предиктором временного ряда во многом зависит от обучающей выборки, функции оценки и используемого семейства адаптивных предикторов, поэтому проблемы их выбора являются одними из наиболее важных. Большое значение при решении задачи предсказания временного ряда отводится квалификации и опыту исследователя, формулирующему гипотезы о характере зависимостей во временном ряде на основе априорных сведении о задаче.
