В библиотеку

Источник: http://paukoff.fromru.com/neuro/wneuro/index.html

ПРОГНОЗИРОВАНИЕ С ПОМОЩЬЮ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ

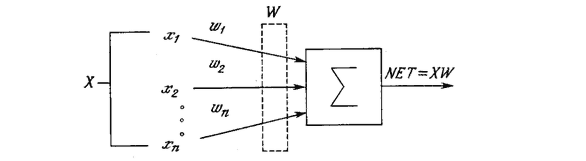
Дмитрий Пауков

Работа посвящена изучению искусственных нейронных сетей, их применению при решении задач в различных сферах человеческой деятельности, в частности - прогнозирование временных рядов (курса валют).

Приводится описание нейронных сетей, принципов их устройства и работы. Рассмотрены модели нейросетей и способы их обучения. Особое внимание уделяется нейросетям обратного распространения и алгоритму их обучения. Описан метод, по средствам которого задачу прогнозирования можно решать с применением нейросетевых технологий. Приводится программная реализация такой нейросети обратного распространения с описанием программной модели, созданной по принципам объектно-ориентированного программирования в среде Delphi 5.

На основании изложенного материала рассмотрено прогнозирование курса валют (украинской гривны к доллару США).

ВВЕДЕНИЕ

Время - это одно из самых интересных понятий, которые интересуют человека с Древних времен. Понять и подчинить себе время человечество стремилось всегда, потому что знание будущего дает невиданную силу принятия решений в различных областях человеческой деятельности. Вопрос определения будущего был и остается актуальным по сегодняшний день. Большой интерес представляют задачи прогнозирования погоды по результатам соответствующих атмосферных измерений, селекционирования новых видов растений и животных, определений возможностей индивидуумов в определенных областях с помощью соответствующей системы контрольных тестов и т.д. Особо важное значение прогнозирование имеет в таких областях, как индустрия, экономика, коммерция (прогнозирование экономических показателей, динамики цен на тот или иной продукт, курса акций на какое-то время вперед и т.д.).

Однако создать машину времени человек не может, мы знаем, что было в прошлом, но совершенно точно утверждать положение вещей в будущем не дано никому из нас. Несмотря на это, люди всегда стремились предугадать будущее, применяя при этом самые различные способы: в простом народе с давних времен популярны народные приметы, математики используют для этого более формальные методы и способы прогнозирования - они применяют статистические и вероятностные характеристики, по которым возможно с определенной вероятностью утверждать, что будущее событие произойдет или нет.

Наряду с традиционными методами прогнозирования сегодня бурно развивается теория искусственных нейронных сетей, которая хорошо зарекомендовала себя в области управления, там, где необходимо применение человеческого интеллекта, в частности при решении задач прогнозирования.

Это научное направление родилось на стыке таких наук как нейробиология, химия, физика, математика, информатика, философия, психология и др. интерес к нейронным сетям был вызван как теоретическими, так и прикладными достижениями в этой области. Нейросети неожиданно открыли возможности использования вычислений в сферах, до этого относящихся лишь к области человеческого интеллекта, возможности создания машин, способность которых учиться и запоминать удивительным образом напоминает мыслительные процессы человека.

Искусственные нейронные сети состоят из элементов, функциональные возможности которых аналогичны большинству элементарных функций биологического нейрона. Эти элементы затем организуются по способу, который может соответствовать (или не соответствовать) анатомии мозга. Несмотря на такое поверхностное сходство, искусственные нейронные сети демонстрируют удивительное число свойств присущих мозгу. Например, они обучаются на основе опыта, обобщают предыдущие прецеденты на новые случаи и извлекают существенные свойства из поступающей информации, содержащей излишние данные.

Несмотря на такое функциональное сходство, даже самый оптимистичный их защитник не предположит, что в скором будущем искусственные нейронные сети будут дублировать функции человеческого мозга. Реальный «интеллект», демонстрируемый самыми сложными нейронными сетями, находится ниже уровня дождевого червя, и энтузиазм должен быть умерен в соответствии с современными реалиями. Однако равным образом было бы неверным игнорировать удивительное сходство в функционировании некоторых нейронных сетей с человеческим мозгом. Эти возможности, как бы они ни были ограничены сегодня, наводят на мысль, что глубокое проникновение в человеческий интеллект, а также множество революционных приложений, могут быть не за горами.

Искусственные нейронные сети могут менять свое поведение в зависимости от внешней среды. Этот фактор в большей степени, чем любой другой, ответствен за тот интерес, который они вызывают. После предъявления входных сигналов (возможно, вместе с требуемыми выходами) они самонастраиваются, чтобы обеспечивать требуемую реакцию. Было разработано множество обучающих алгоритмов, каждый со своими сильными и слабыми сторонами. Все еще существуют проблемы относительно того, чему нейросеть может обучиться и как обучение должно проводиться.

Отклик сети после обучения может быть до некоторой степени нечувствителен к небольшим изменениям входных сигналов. Эта внутренне присущая способность видеть образ сквозь шум и искажения жизненно важна для распознавания образов в реальном мире. Она позволяет преодолеть требование строгой точности, предъявляемое обычным компьютером, и открывает путь к системе, которая может иметь дело с тем несовершенным миром, в котором мы живем. Важно отметить, что искусственная нейронная сеть делает обобщения автоматически благодаря своей структуре, а не с помощью использования «человеческого интеллекта» в форме специально написанных компьютерных программ.

Некоторые из искусственных нейронных сетей обладают способностью извлекать сущность из входных сигналов. Например, сеть может быть обучена на последовательность искаженных версий буквы «А». После соответствующего обучения предъявление такого искаженного примера приведет к тому, что сеть породит букву совершенной формы. В некотором смысле она научится порождать то, что никогда не видела.

Эта способность извлекать идеальное из несовершенных входов ставит интересные философские вопросы. Она напоминает концепцию идеалов, выдвинутую Платоном в его «Республике». Во всяком случае, способность извлекать идеальные прототипы является у людей весьма ценным качеством.

Искусственные нейронные сети не являются панацеей. Они, очевидно, не годятся для выполнения таких задач, как начисление заработной платы. Похоже, однако, что им будет отдаваться предпочтение в большом классе задач распознавания образов, прогнозирования, создание ассоциативной памяти, экономики, управления объектами, с которыми плохо или вообще не справляются обычные компьютеры.

1 ПОСТАНОВКА ЗАДАЧИ

В различных областях человеческой деятельности часто возникают ситуации, когда по имеющейся информации (данным), обозначим ее X, требуется предсказать (спрогнозировать, оценить) некоторую величину Y, стохастически связанную с X (то есть X и Y имеют некоторое распределение L(X,Y)), но которую непосредственно измерить невозможно (например, Y может относиться к будущему, а X - к настоящему). Так, например, может представлять интерес прогноз успеваемости первокурсников очередного набора по оценкам, полученным ими на вступительных экзаменах. Здесь X - средний балл студентов на вступительных экзаменах, а Y - средний балл по итогам, скажем, первой сессии; при этом совместное распределение X и Y можно в принципе определить (оценить) по аналогичным данным за прошлые годы.

В общем случае X означает некоторую совокупность {X₁, X₂,…} наблюдаемых случайных величин, которые в рассматриваемом контексте называются предсказывающими (или прогнозными) переменными, и задача состоит в построении такой функции Ф(Х), которую можно было бы использовать в качестве оценки для прогнозируемой величины Y:Ф(Х)=Y (т.е. чтобы она была в каком-то смысле "близка" к Y); такие функции Ф(Х) называют предикторами величины Y по X. Разработка методов построения оптимальных (в том или ином смысле) предикторов и составляет главную задачу прогнозирования.

Если совокупность величин {X₁, X₂, …, X_n} представляет собой значения какого-либо параметра, изменяющегося во времени, то такую совокупность называют временным рядом, при этом каждое значение соответствует значению параметра в конкретное время t₁, t₂, …,t_n. Задача прогнозирования в этом случае заключается в определении значения измеряемой величины X в момент времени t_n+1, t_n+2, t_n+3,…, то есть для выполнения прогнозирования необходимо выявить закономерность этого временного ряда.

Различают многошаговый и одношаговый прогноз.

Многошаговым прогнозом называют долгосрочный прогноз, цель которого состоит в определении основного тренда, для некоторого фиксированного промежутка времени в будущем. При этом прогнозирующая система (в нашем случае - нейронная сеть) использует полученные прогнозные значения временного ряда для выполнения дальнейшего прогноза, то есть использует их как входные данные.

Одношаговым прогнозированием называют краткосрочный прогноз (на один шаг), при этом для получения прогнозированной величины используют только фактические данные. Ясно, что одношаговое прогнозирование более точно, но оно не позволяет выполнять долгосрочные прогнозы.

Целью данной работы есть разработка системы, которая могла бы выполнять одношаговое и многошаговое прогнозирование и использовала технологии искусственных нейронных сетей; при этом будет показано каким образом задача прогнозирования сводится к задаче распознавания образов (см. раздел 4).

2 ОБЗОР КЛАССИЧЕСКИХ МЕТОДОВ И СРЕДСТВ ПРОГНОЗИРОВАНИЯ

2.1 Статистические методы

Статистические модели - важный класс моделей, которые предлагает математика исследователю. С помощью этих моделей описываются явления, в которых присутствуют статистические факторы, не позволяющие объяснить явление в чисто детерминистских терминах. Типичные примеры такого рода моделей представляют временные ряды (см. раздел 1) в экономике и финансовой сфере, имеющие тренд-циклическую компоненту и случайную составляющую. Хочет того или нет, исследователь не может исключить случайную составляющую и должен строить свои выводы, учитывая ее наличие.

Прогнозирование, нахождение скрытых периодичностей в данных, анализ зависимостей, оценка рисков при принятии решений и другие задачи решаются в рамках статистических моделей.

Статистика оперирует перечисленными ниже понятиями.

Генеральная совокупность - множество всех объектов в исследованиях.

Выборка - подмножество генеральной совокупности, непосредственно участвующее в статистической обработке. Выборка должна быть объективной, иначе результаты будут искажены. Способы отбора выборок: случайный, систематический (например, каждый седьмой), экспертный, районированный. Выборку задают в виде статистического ряда - последовательности чисел.

По выборке строят гистограмму - графическое изображение статистического ряда, статистический аналог функции плотности в теории вероятностей. Свойство функции плотности совпадает с аналогичным свойством гистограммы: площадь гистограммы равна единице. По виду гистограммы делают предположение о характере закона распределения исследуемой величины и уточняют параметры этого распределения одним из методов: метод моментов, метод максимального правдоподобия, метод наименьших квадратов, также оценивают математическое ожидание, дисперсию, находят доверительный интервал для этих оценок. Для проверки непротиворечивости данных предположенному закону с уточненными параметрами используют критерий Пирсона или Колмогорова.

Теория стохастического прогнозирования [1] изучает методы построения предикторов (см. раздел 1). Для построения этой теории, прежде всего, требуется уточнить смысл приближенного равенства Ф(Х)≈Y. Если Ф(Х) используется для предсказания величины Y, то одной из разумных мер расхождения между ними является (Ф(Х)-Y)², или квадратичная ошибка, но так как величина Y неизвестна, то для измерения точности предиктора Ф используется среднеквадратичная ошибка ∆Ф=М(Ф(Х)-Y)², где М - знак математического ожидания. Среднеквадратическая ошибка - мера, традиционно используемая в теории стохастического прогнозирования, хотя в принципе можно было бы использовать и другие меры точности, например среднюю абсолютную ошибку. Предиктор, минимизирующий среднеквадратичную ошибку в заданном классе предикторов, называют оптимальным предиктором или прогнозом.

2.2 Программный пакет STATISTICA

Пакет STATISTICA фирмы StatSoft является интегрированной системой комплексного статистического анализа и обработки данных в среде Windows и занимает устойчивое лидирующее положение на рынке статистического программного обеспечения. Она полностью согласована со всеми стандартами Windows. Отдельные модули, из которых построена система, являются полноценными Windows-приложениями.

Прогнозирование моделей авторегрессии и проинтегрированного скользящего среднего [1] имеет методику, реализуемую в следующей последовательности:

1.     идентификация, или определение модели, которая описывает наблюдаемый временной ряд;

2.     оценка параметров модели;

3.     исследование адекватности модели;

4.     прогноз.

Каждый из этапов методики легко доступен в пакете STATISTICA. Исследователь не испытывает перегрузок, связанных с подготовкой данных, проверкой результатов, построением графиков, рассмотрением альтернативных вариантов - все необходимые инструменты у него под рукой. Например, исследование и прогнозирование временных рядов в рамках ARIMA - Авторегрессия и проинтегрированное скользящее среднее, - реализованные в системе STATISTICA, соответствуют методическим основам Бокса и Дженкинса [1]. Образно можно сказать, что реализованный в системе диалог ARIMA является перенесением методологии Бокса и Дженкинса из мира математических идей и моделей в мир современных компьютерных технологий.

Большим достоинством системы является наличие встроенного языка STATISTICA BASIC, позволяющего моделировать временные ряды, оценивать качество прогноза, риск при использовании определенной стратегии игры.

Несмотря на существование теории стохастического прогнозирования, программных средств реализующих эту теорию большой, интерес представляют иные подходы к решению проблемы прогнозирования - нейронные сети способны распараллеливать процесс и поэтому работать эффективнее, а кроме этого они могут таить в себе еще неоткрытые возможности.

3 НЕЙРОСЕТЕВЫЕ ТЕХНОЛОГИИ

3.1 История развития нейронных сетей

Людей всегда интересовало их собственное мышление. Это думанье мозга о себе самом является, возможно, отличительной чертой человека. Имеется множество размышлений о природе мышления, простирающихся от духовных до анатомических. Обсуждение этого вопроса, протекавшее в горячих спорах философов и теологов с физиологами и анатомами, принесло мало пользы, так как сам предмет весьма труден для изучения. Те, кто опирался на самоанализ и размышление, пришли к выводам, не отвечающим уровню строгости физических наук. Экспериментаторы же нашли, что мозг труден для наблюдения и ставит в тупик своей организацией. Короче говоря, мощные методы научного исследования, изменившие наш взгляд на физическую реальность, оказались бессильными в понимании самого человека.

Нейробиологи и нейроанатомы достигли значительного прогресса. Усердно изучая структуру и функции нервной системы человека, они многое поняли в «электропроводке» мозга, но мало узнали о его функционировании. В процессе накопления ими знаний выяснилось, что мозг имеет ошеломляющую сложность. Сотни миллиардов нейронов, каждый из которых соединен с сотнями или тысячами других нейронов, образуют систему, далеко превосходящую наши самые смелые мечты о суперкомпьютерах.

Лучшее понимание функционирования нейрона и картины его связей позволило исследователям создать математические модели для проверки своих теорий. Эксперименты теперь могут проводиться на цифровых компьютерах без привлечения человека или животных, что решает многие практические и морально-этические проблемы. В первых же работах выяснилось, что эти модели не только повторяют функции мозга, но и способны выполнять функции, имеющие свою собственную ценность. Поэтому возникли и остаются в настоящее время две взаимно обогащающие друг друга цели нейронного моделирования: первая – понять функционирование нервной системы человека на уровне физиологии и психологии и вторая – создать вычислительные системы (искусственные нейронные сети), выполняющие функции, сходные с функциями мозга.

Параллельно с прогрессом в нейроанатомии и нейрофизиологии психологами были созданы модели человеческого обучения. Одной из таких моделей, оказавшейся наиболее плодотворной, была модель Д. Хэбба [2], который в 1949г. предложил закон обучения, явившийся стартовой точкой для алгоритмов обучения искусственных нейронных сетей. Дополненный сегодня множеством других методов он продемонстрировал ученым того времени, как сеть нейронов может обучаться.

В пятидесятые и шестидесятые годы группа исследователей, объединив эти биологические и физиологические подходы, создала первые искусственные нейронные сети. Выполненные первоначально как электронные сети, они были позднее перенесены в более гибкую среду компьютерного моделирования, сохранившуюся и в настоящее время. Первые успехи вызвали взрыв активности и оптимизма. Минский, Розенблатт, Уидроу и другие разработали сети, состоящие из одного слоя искусственных нейронов. Часто называемые персептронами, они были использованы для такого широкого класса задач, как предсказание погоды, анализ электрокардиограмм и искусственное зрение. В течение некоторого времени казалось, что ключ к интеллекту найден, и воспроизведение человеческого мозга является лишь вопросом конструирования достаточно большой сети.

Но эта иллюзия скоро рассеялась. Нейросети не могли решать задачи, внешне весьма сходные с теми, которые они успешно решали. С этих необъяснимых неудач начался период интенсивного анализа. М.Минский, используя точные математические методы, строго доказал ряд теорем, относящихся к функционированию сетей.

Его исследования привели к написанию книги [3], в которой он вместе с Пайпертом доказал, что используемые в то время однослойные сети теоретически неспособны решить многие простые задачи, в том числе реализовать функцию «Исключающее ИЛИ». Минский также не был оптимистичен относительно потенциально возможного здесь прогресса.

Блеск и строгость аргументации Минского, а также его престиж породили огромное доверие к книге – ее выводы были неуязвимы. Разочарованные исследователи оставили поле исследований ради более обещающих областей, а правительства перераспределили свои субсидии, и искусственные нейронные сети были забыты почти на два десятилетия.

Однако несколько наиболее настойчивых ученых, таких как Кохонен, Гроссберг, Андерсон продолжили исследования. Наряду с плохим финансированием и недостаточной оценкой, ряд исследователей испытывал затруднения с публикациями. Поэтому исследования, опубликованные в семидесятых и начале восьмидесятых годов, разбросаны в массе различных журналов, некоторые из которых малоизвестны. Постепенно появился теоретический фундамент, на основе которого сегодня конструируются наиболее мощные многослойные сети. За последние несколько лет теория стала применяться в прикладных областях, и появились новые корпорации, занимающиеся коммерческим использованием этой технологии.

3.2 Искусственные нейронные сети

Искусственные нейронные сети чрезвычайно разнообразны по своим конфигурациям. Несмотря на такое разнообразие, сетевые парадигмы имеют много общего.

 К сожалению, для искусственных нейронных сетей еще нет опубликованных стандартов и устоявшихся терминов, обозначений и графических представлений. Порой идентичные сетевые парадигмы, представленные различными авторами, кажутся далекими друг от друга. В данной работе выбраны обозначения и графические представления наиболее широко используемые в настоящее время.

3.2.1 Биологический прототип нейрона

Развитие искусственных нейронных сетей вдохновляется биологией, то есть, рассматривая сетевые конфигурации и алгоритмы, исследователи мыслят их в терминах организации мозговой деятельности. Но на этом аналогия может и закончиться. Наши знания о работе мозга ограничены. Поэтому разработчикам сетей приходится выходить за пределы современных биологических знаний в поисках структур, способных выполнять полезные функции. Во многих случаях это приводит к необходимости отказа от биологического правдоподобия, мозг становится просто метафорой, и создаются сети, невозможные в живой материи или требующие неправдоподобно больших допущений об анатомии и функционировании мозга.

Несмотря на то, что связь с биологией слаба и зачастую несущественна, искусственные нейронные сети продолжают сравниваться с мозгом. Их функционирование часто напоминает человеческое познание, поэтому трудно избежать этой аналогии. К сожалению, такие сравнения неплодотворны и создают неоправданные ожидания, неизбежно ведущие к разочарованию.

Несмотря на сделанные предупреждения, полезно все же знать кое-что о нервной системе млекопитающих, так как она успешно решает задачи, к выполнению которых лишь стремятся искусственные системы. Нервная система человека, построенная из элементов, называемых нейронами, имеет ошеломляющую сложность. Около 10¹¹ нейронов участвуют в примерно 10¹⁵ передающих связях, имеющих длину метр и более. Каждый нейрон обладает многими качествами, общими с другими элементами тела, но его уникальной способностью является прием, обработка и передача электрохимических сигналов по нервным путям, которые образуют коммуникационную систему мозга.

Cтруктура пары типичных биологических нейронов: дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы подводятся к телу нейрона. Здесь они суммируются, причем одни входы стремятся возбудить нейрон, другие – воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам. У этой основной функциональной схемы много усложнений и исключений, тем не менее большинство искусственных нейронных сетей моделируют лишь эти простые свойства.

3.2.2 Искусственный нейрон

Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рисунке 3.2 представлена модель, реализующая эту идею. Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит эта конфигурация. Здесь множество входных сигналов, обозначенных x₁, x₂,…, x_n, поступает на искусственный нейрон. Эти входные сигналы, в совокупности, обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес w₁, w₂,…, w_n, и поступает на суммирующий блок, обозначенный Σ. Каждый вес соответствует «силе» одной биологической синаптической связи. (Множество весов в совокупности обозначается вектором W.) Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть NET. В векторных обозначениях это может быть компактно записано следующим образом: NET = XW.

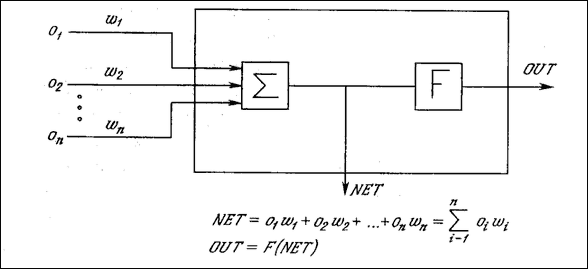
Рисунок 3.2 - Искусственный нейрон

Сигнал NET далее, как правило, преобразуется активационной функцией F и дает выходной нейронный сигнал OUT. Активационная функция может быть обычной линейной функцией OUT = K*NET, где К – постоянная, пороговой функции, или же функцией, более точно моделирующей нелинейную передаточную характеристику биологического нейрона и представляющей нейронной сети большие возможности.

Рисунок 3.3 - Искусственный нейрон с активационной функцией

На рисунке 3.3 блок, обозначенный F, принимает сигнал NET и выдает сигнал OUT. Если блок F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется «сжимающей» функцией. В качестве «сжимающей» функции часто используется логистическая или «сигмоидальная» (S-образная) функция. Эта функция математически выражается как F(x) = 1/(1 + е^-x). Таким образом,

 .

По аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT к вызвавшему его небольшому приращению величины NET. Он выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Гроссберг (1973) обнаружил, что подобная нелинейная характеристика решает поставленную им дилемму шумового насыщения. Каким образом одна и та же сеть может обрабатывать как слабые, так и сильные сигналы? Слабые сигналы нуждаются в большом сетевом усилении, чтобы дать пригодный к использованию выходной сигнал. Однако усилительные каскады с большими коэффициентами усиления могут привести к насыщению выхода шумами усилителей (случайными флуктуациями), которые присутствуют в любой физически реализованной сети. Сильные входные сигналы в свою очередь также будут приводить к насыщению усилительных каскадов, исключая возможность полезного использования выхода. Центральная область логистической функции, имеющая большой коэффициент усиления, решает проблему обработки слабых сигналов, в то время как области с падающим усилением на положительном и отрицательном концах подходят для больших возбуждений. Таким образом, нейрон функционирует с большим усилением в широком диапазоне уровня входного сигнала.

 .

Другой широко используемой активационной функцией является гиперболический тангенс. По форме она сходна с логистической функцией и часто используется биологами в качестве математической модели активации нервной клетки. В качестве активационной функции искусственной нейронной сети она записывается следующим образом:

Подобно логистической функции гиперболический тангенс является S-образной функцией, но он симметричен относительно начала координат, и в точке NET = 0 значение выходного сигнала OUT равно нулю. В отличие от логистической функции гиперболический тангенс принимает значения различных знаков, что оказывается выгодным для ряда сетей (обратного распространения).

Рассмотренная простая модель искусственного нейрона игнорирует многие свойства своего биологического двойника. Например, она не принимает во внимание задержки во времени, которые воздействуют на динамику системы. Входные сигналы сразу же порождают выходной сигнал. И, что более важно, она не учитывает воздействий функции частотной модуляции или синхронизирующей функции биологического нейрона, которые ряд исследователей считают решающими.

Несмотря на эти ограничения, сети, построенные из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую систему. Только время и исследования смогут ответить на вопрос, являются ли подобные совпадения случайными или следствием того, что в модели верно схвачены важнейшие черты биологического нейрона.

3.2.3 Однослойные искусственные нейронные сети

Хотя один нейрон и способен выполнять простейшие процедуры распознавания, сила нейронных вычислений проистекает от соединений нейронов в сетях. Простейшая сеть состоит из группы нейронов, образующих слой, как показано в правой части рисунка 3.5. Отметим, что вершины-круги слева служат лишь для распределения входных сигналов. Они не выполняют каких- либо вычислений, и поэтому не будут считаться слоем. По этой причине они обозначены кругами, чтобы отличать их от вычисляющих нейронов, обозначенных квадратами. Каждый элемент из множества входов Х отдельным весом соединен с каждым искусственным нейроном. Каждый нейрон выдает взвешенную сумму входов в сеть. В искусственных и биологических сетях многие соединения могут отсутствовать, все соединения показаны в целях общности. Могут иметь место также соединения между выходами и входами элементов в слое.

Рисунок 3.5 - Однослойная нейронная сеть

Удобно считать веса элементами матрицы W. Матрица имеет т строк и п столбцов, где m – число входов, а n – число нейронов. Например, w_2,3 – это вес, связывающий третий вход со вторым нейроном. Таким образом, вычисление выходного вектора N, компонентами которого являются выходы OUT нейронов, сводится к матричному умножению N=XW, где N и Х – векторы-строки.

3.2.4 Многослойные искусственные нейронные сети

Более крупные и сложные нейронные сети обладают, как правило, и большими вычислительными возможностями. Хотя созданы сети всех конфигураций, какие только можно себе представить, послойная организация нейронов копирует слоистые структуры определенных отделов мозга. Оказалось, что такие многослойные сети обладают большими возможностями, чем однослойные, и в последние годы были разработаны алгоритмы для их обучения.

Многослойные сети могут образовываться каскадами слоев. Выход одного слоя является входом для последующего слоя.

Многослойные сети могут привести к увеличению вычислительной мощности по сравнению с однослойной сетью лишь в том случае, если активационная функция между слоями будет нелинейной. Вычисление выхода слоя заключается в умножении входного вектора на первую весовую матрицу с последующим умножением (если отсутствует нелинейная активационная функция) результирующего вектора на вторую весовую матрицу: (XW₁)W₂. Так как умножение матриц ассоциативно, то X(W₁W₂). Это показывает, что двухслойная линейная сеть эквивалентна одному слою с весовой матрицей, равной произведению двух весовых матриц. Следовательно, любая многослойная линейная сеть может быть заменена эквивалентной однослойной сетью. Таким образом, для расширения возможностей сетей по сравнению с однослойной сетью необходима нелинейная активационная функция.

У сетей, рассмотренных до сих пор, не было обратных связей, т. е. соединений, идущих от выходов некоторого слоя к входам этого же слоя или предшествующих слоев. Этот специальный класс сетей, называемых сетями без обратных связей или сетями прямого распространения, представляет интерес и широко используется. Сети более общего вида, имеющие соединения от выходов к входам, называются сетями с обратными связями. У сетей без обратных связей нет памяти, их выход полностью определяется текущими входами и значениями весов. В некоторых конфигурациях сетей с обратными связями предыдущие значения выходов возвращаются на входы; выход, следовательно, определяется как текущим входом, так и предыдущими выходами. По этой причине сети с обратными связями могут обладать свойствами, сходными с кратковременной человеческой памятью.

3.3 Обучение искусственных нейронных сетей

Среди всех интересных свойств искусственных нейронных сетей ни одно не захватывает так воображения, как их способность к обучению. Их обучение до такой степени напоминает процесс интеллектуального развития человеческой личности, что может показаться, что достигнуто глубокое понимание этого процесса. Возможности обучения искусственных нейронных сетей ограниченны, и нужно решить много сложных задач, чтобы определить, на правильном ли пути мы находимся. Тем не менее, уже получены убедительные достижения, такие как «говорящая сеть» Сейновского [2], и возникает много других практических применений.

Нейросеть обучается, чтобы для некоторого множества входов давать желаемое (или, по крайней мере, сообразное с ним) множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор.

Различают стратегии обучения: "обучение с учителем" и "обучение без учителя".

"Обучение с учителем" предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно нейросеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход нейросети и сравнивается с соответствующим целевым вектором, разность (ошибка) с помощью обратной связи подается в сеть и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

Несмотря на многочисленные прикладные достижения, обучение с учителем критиковалось за свою биологическую неправдоподобность. Трудно вообразить обучающий механизм в мозге, который бы сравнивал желаемые и действительные значения выходов, выполняя коррекцию с помощью обратной связи. Если допустить подобный механизм в мозге, то откуда тогда возникают желаемые выходы? Обучение без учителя является намного более правдоподобной моделью обучения в биологической системе. Развитая Кохоненом [4] и многими другими, она не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса нейросети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью.

Большинство современных алгоритмов обучения выросло из концепций Хэбба [5]. Им предложена модель обучения без учителя, в которой синаптическая сила (вес) возрастает, если активированы оба нейрона, источник и приемник. Таким образом, часто используемые пути в сети усиливаются и феномен привычки и обучения через повторение получает объяснение.

3.4 Нейросети обратного распространения

3.4.1 Введение

Долгое время не было теоретически обоснованного алгоритма для обучения многослойных искусственных нейронных сетей. А так как возможности представления с помощью однослойных нейронных сетей оказались весьма ограниченными, то и вся область в целом пришла в упадок.

Разработка алгоритма обратного распространения сыграла важную роль в возрождении интереса к искусственным нейронным сетям. Обратное распространение – это систематический метод для обучения многослойных искусственных нейронных сетей. Он имеет солидное математическое обоснование. Несмотря на некоторые ограничения, процедура обратного распространения сильно расширила область проблем, в которых могут быть использованы искусственные нейронные сети, и убедительно продемонстрировала свою мощь.

Интересна история разработки процедуры. В [6] было дано ясное и полное описание процедуры. Вскоре выяснилось, что еще раньше метод был описан в [7]. Авторы работы [6] сэкономили бы свои усилия, знай они о работе [7]. Хотя подобное дублирование является обычным явлением для каждой научной области, в искусственных нейронных сетях положение с этим намного серьезнее из-за пограничного характера самого предмета исследования. Исследования по нейронным сетям публикуются в столь различных книгах и журналах, что даже самому квалифицированному исследователю требуются значительные усилия, чтобы быть осведомленным о всех важных работах в этой области.

Рисунок 3.7 - Искусственный нейрон с активационнной функцией

На рисунке 3.7 показан нейрон, используемый в качестве основного строительного блока в сетях обратного распространения. Подается множество входов, идущих либо извне, либо от предшествующего слоя. Каждый из них умножается на вес, и произведения суммируются. Эта сумма, обозначаемая NET, должна быть вычислена для каждого нейрона сети. После того, как величина NET вычислена, она модифицируется с помощью активационной функции и получается сигнал OUT.

 . (3.1)

Как показывает уравнение (3.2), эта функция, называемая сигмоидом, весьма удобна, так как имеет простую производную, что используется при реализации алгоритма обратного распространения.

 . (3.2)

Сигмоид, который иногда называется также логистической, или сжимающей функцией, сужает диапазон изменения NET так, что значение OUT лежит между нулем и единицей. Как указывалось выше (см 3.2.4), многослойные нейронные сети обладают большей представляющей мощностью, чем однослойные, только в случае присутствия нелинейности. Сжимающая функция обеспечивает требуемую нелинейность.

В действительности имеется множество функций, которые могли бы быть использованы. Для алгоритма обратного распространения требуется лишь, чтобы функция была всюду дифференцируема. Сигмоид удовлетворяет этому требованию. Его дополнительное преимущество состоит в автоматическом контроле усиления. Для слабых сигналов (величина NET близка к нулю) кривая вход-выход имеет сильный наклон, дающий большое усиление. Когда величина сигнала становится больше, усиление падает. Таким образом, большие сигналы воспринимаются сетью без насыщения, а слабые сигналы проходят по сети без чрезмерного ослабления.

В литературе нет единообразия относительно того, как считать число слоев в таких сетях. Одни авторы используют число слоев нейронов (включая несуммирующий входной слой), другие – число слоев весов [2]. Так как последнее определение функционально описательное, то будем использовать его. Согласно этому определению, сеть на рисунке 3.9 рассматривается как двухслойная. Нейрон объединен с множеством весов, присоединенных к его входу. Таким образом, веса первого слоя оканчиваются на нейронах первого слоя. Вход распределительного слоя считается нулевым слоем.

Процедура обратного распространения применима к сетям с любым числом слоев. Однако для того, чтобы продемонстрировать алгоритм, достаточно двух слоев.

3.4.2 Обучение нейросетей обратного распространения

Целью обучения сети является такая подстройка ее весов, чтобы подача на нейросеть некоторого множества входов приводила к требуемому множеству выходов. Для краткости эти множества входов и выходов будем называть векторами. При обучении предполагается, что для каждого входного вектора существует парный ему целевой вектор, задающий требуемый выход. Вместе они называются обучающей парой. Как правило, нейросеть обучается на многих парах.

Перед началом обучения всем весам должны быть присвоены небольшие начальные значения, выбранные случайным образом. Это гарантирует, что в сети не произойдет насыщения большими значениями весов, и предотвращает ряд других патологических случаев. Например, если всем весам придать одинаковые начальные значения, а для требуемого функционирования нужны неравные значения, то сеть не сможет обучиться.

Обучение сети обратного распространения требует выполнения следующих операций:

Выбрать очередную обучающую пару из обучающего множества; подать входной вектор на вход сети.

Вычислить выход сети.

Вычислить разность между выходом сети и требуемым выходом (целевым вектором обучающей пары).

Подкорректировать веса сети так, чтобы минимизировать ошибку.

Повторять шаги с 1 по 4 для каждого вектора обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого уровня.

Операции, выполняемые шагами 1 и 2, сходны с теми, которые выполняются при функционировании уже обученной сети, т. е. подается входной вектор и вычисляется получающийся выход. Вычисления выполняются послойно. На рисунке 3.9 сначала вычисляются выходы нейронов слоя j, затем они используются в качестве входов слоя k, вычисляются выходы нейронов слоя k, которые и образуют выходной вектор сети.

На шаге 3 каждый из выходов сети, которые на рисунке 3.9 обозначены OUT, вычитается из соответствующей компоненты целевого вектора, чтобы получить ошибку. Эта ошибка используется на шаге 4 для коррекции весов нейросети, причем знак и величина изменений весов определяются алгоритмом обучения (см. ниже).

После достаточного числа повторений этих четырех шагов разность между действительными выходами и целевыми выходами должна уменьшиться до приемлемой величины, при этом говорят, что нейросеть обучилась. Только после этого нейросеть используется для распознавания и веса в ней не изменяются.

На шаги 1 и 2 можно смотреть как на «проход вперед», так как сигнал распространяется по сети от входа к выходу. Шаги 3, 4 составляют «обратный проход», здесь вычисляемый сигнал ошибки распространяется обратно по сети и используется для подстройки весов. Эти два прохода теперь будут детализированы и выражены в более математической форме.

3.4.2.1 Проход вперед

Шаги 1 и 2 могут быть выражены в векторной форме следующим образом: подается входной вектор Х и на выходе получается вектор Y. Векторная пара вход-цель Х и Т берется из обучающего множества. Вычисления проводятся над вектором X, чтобы получить выходной вектор Y.

Как мы видели, вычисления в многослойных сетях выполняются слой за слоем, начиная с ближайшего к входу слоя. Величина NET каждого нейрона первого слоя вычисляется как взвешенная сумма входов нейрона. Затем активационная функция F «сжимает» NET и дает величину OUT для каждого нейрона в этом слое. Когда множество выходов слоя получено, оно является входным множеством для следующего слоя. Процесс повторяется слой за слоем, пока не будет получено заключительное множество выходов сети.

Этот процесс может быть выражен в сжатой форме с помощью векторной нотации. Веса между нейронами могут рассматриваться как матрица W. Например, вес от нейрона 8 в слое 2 к нейрону 5 слоя 3 обозначается w_8,5. Тогда NET-вектор слоя N может быть выражен не как сумма произведений, а как произведение Х и W. В векторном обозначении N=XW. Покомпонентным применением функции F к NET-вектору N получается выходной вектор О. Таким образом, для данного слоя вычислительный процесс описывается следующим выражением:

 О = F(XW) (3.3)

Выходной вектор одного слоя является входным вектором для следующего, поэтому вычисление выходов последнего слоя требует применения уравнения (3.3) к каждому слою от входа сети к ее выходу.

3.4.2.2 Обратный проход

3.4.2.2.1 Подстройка весов выходного слоя

Так как для каждого нейрона выходного слоя задано целевое значение, то подстройка весов легко осуществляется с использованием модифицированного дельта-правила [2]. Внутренние слои называют «скрытыми слоями», для их выходов не имеется целевых значений для сравнения. Поэтому обучение усложняется.

 δ = OUT(1 – OUT)(Target – OUT) (3.4)

Затем δ умножается на величину OUT нейрона j, из которого выходит рассматриваемый вес. Это произведение в свою очередь умножается на коэффициент скорости обучения η (обычно от 0.01 до 1.0), и результат прибавляется к весу. Такая же процедура выполняется для каждого веса от нейрона скрытого слоя к нейрону в выходном слое.

Следующие уравнения иллюстрируют это вычисление:

 Δw_pq,k = η δ_q,k OUT (3.5)

 w_pq,k(n+1) = w_pq,k(n) + Δw_pq,k (3.6)

где w_pq,k(n) – величина веса от нейрона p в скрытом слое к нейрону q в выходном слое на шаге n (до коррекции); что индекс k относится к слою, в котором заканчивается данный вес, т. е. с которым он объединен; w_pq,k(n+1) – величина веса на шаге n+1 (после коррекции); δ_q,k – величина δ для нейрона q, в выходном слое k; OUT_p,j – величина OUT для нейрона р в скрытом слое j.

3.4.2.2.2 Подстройка весов скрытого слоя

Рассмотрим один нейрон в скрытом слое, предшествующем выходному слою. При проходе вперед этот нейрон передает свой выходной сигнал нейронам в выходном слое через соединяющие их веса. Во время обучения эти веса функционируют в обратном порядке, пропуская величину δ от выходного слоя назад к скрытому слою. Каждый из этих весов умножается на величину δ нейрона, к которому он присоединен в выходном слое. Величина δ, необходимая для нейрона скрытого слоя, получается суммированием всех таких произведений и умножением на производную сжимающей функции:

.Для каждого нейрона в данном скрытом слое должно быть вычислено δ и подстроены все веса, ассоциированные с этим слоем. Этот процесс повторяется слой за слоем по направлению к входу, пока все веса не будут подкорректированы.

С помощью векторных обозначений операция обратного распространения ошибки может быть записана значительно компактнее. Обозначим множество величин δ выходного слоя через D_k и множество весов выходного слоя как массив W_k. Чтобы получить D_j, δ-вектор выходного слоя, достаточно следующих двух операций:

1.     Умножить о-вектор выходного слоя D_k на транспонированную матрицу весов W^’_k, соединяющую скрытый уровень с выходным уровнем.

2.     Умножить каждую компоненту полученного произведения на производную сжимающей функции соответствующего нейрона в скрытом слое.

В символьной записи

 D_j = D_kW^’_k $[0_j $(I – 0_j)], (3.8)

где оператор $ обозначает покомпонентное произведение векторов, О_j – выходной вектор слоя j и I – вектор, все компоненты которого равны 1.

3.4.2.3 Проблемы обучения нейросетей обратного распространения

Несмотря на многочисленные успешные применения обратного распространения (см. ниже), оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Длительное время обучения может быть результатом неоптимального выбора длины шага. Неудачи в обучении обычно возникают по двум причинам: паралича сети и попадания в локальный минимум.

В процессе обучения нейросети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от этого явления, называемого параличом нейросети, или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.

Обратное распространение использует разновидность градиентного спуска, т. е. осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Статистические методы обучения могут помочь избежать этой ловушки, но они медленны. В [8] предложен метод, объединяющий статистические методы машины Коши с градиентным спуском обратного распространения и приводящий к системе, которая находит глобальный минимум, сохраняя высокую скорость обратного распространения.

Внимательный разбор доказательства сходимости в [9] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость. В [10] описан адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения.

Если сеть учится распознавать буквы, то нет смысла учить «Б», если при этом забывается «А». Процесс обучения должен быть таким, чтобы сеть обучалась на всем обучающем множестве без пропусков того, что уже выучено. В доказательстве сходимости [9] это условие выполнено, но требуется также, чтобы сети предъявлялись все векторы обучающего множества прежде, чем выполняется коррекция весов. Необходимые изменения весов должны вычисляться на всем множестве, а это требует дополнительной памяти; после ряда таких обучающих циклов веса сойдутся к минимальной ошибке. Этот метод может оказаться бесполезным, если сеть находится в постоянно меняющейся внешней среде, так что второй раз один и тот же вектор может уже не повториться. В этом случае процесс обучения может никогда не сойтись, бесцельно блуждая или сильно осциллируя. В этом смысле обратное распространение не похоже на биологические системы.

3.4.2.4 Другие алгоритмические разработки

Добавление нейронного смещения. Во многих случаях желательно наделять каждый нейрон обучаемым смещением. Это позволяет сдвигать начало отсчета логистической функции, давая эффект, аналогичный подстройке порога персептронного нейрона [2], и приводит к ускорению процесса обучения. Эта возможность может быть легко введена в обучающий алгоритм с помощью добавляемого к каждому нейрону веса, присоединенного к+1. Этот вес обучается так же, как и все остальные веса, за исключением того, что подаваемый на него сигнал всегда равен +1, а не выходу нейрона предыдущего слоя.

Импульс. В работе [9] описан метод ускорения обучения для алгоритма обратного распространения, увеличивающий также устойчивость процесса. Этот метод, названный импульсом, заключается в добавлении к коррекции веса члена, пропорционального величине предыдущего изменения веса. Как только происходит коррекция, она «запоминается» и служит для модификации всех последующих коррекций. Уравнения коррекции модифицируются следующим образом:

 Δw_pq,k(n+1)= η δ_q,k OUT_p,j + aΔw_pq,k(n) (3.9)

 w_pq,k(n+1) = w_pq,k(n) + Δw_pq,k(n+1)  (3.10)

где a – коэффициент импульса, обычно устанавливается около 0,9.

Используя метод импульса, нейросеть стремится идти по дну узких оврагов поверхности ошибки (если таковые имеются), а не двигаться от склона к склону. Этот метод, по-видимому, хорошо работает на некоторых задачах, но дает слабый или даже отрицательный эффект на других.

Многими исследователями были предложены улучшения и обобщения описанного выше основного алгоритма обратного распространения. Литература в этой области слишком обширна, чтобы ее можно было здесь охватить. Кроме того, сейчас еще слишком рано давать окончательные оценки. Некоторые из этих подходов могут оказаться действительно фундаментальными, другие же со временем исчезнут.

В [11] описан метод ускорения сходимости алгоритма обратного распространения. Названный обратным распространением второго порядка, он использует вторые производные для более точной оценки требуемой коррекции весов. В [11] показано, что этот алгоритм оптимален в том смысле, что невозможно улучшить оценку, используя производные более высокого порядка. Метод требует дополнительных вычислений по сравнению с обратным распространением первого порядка, и необходимы дальнейшие эксперименты для доказательства оправданности этих затрат.

В [12] описан привлекательный метод улучшения характеристик обучения сетей обратного распространения. В работе указывается, что общепринятый от 0 до 1 динамический диапазон входов и выходов скрытых нейронов неоптимален. Так как величина коррекции веса Δw_pq,k пропорциональна выходному уровню нейрона, порождающего OUT_p,j, то нулевой уровень ведет к тому, что вес не меняется. При двоичных входных векторах половина входов в среднем будет равна нулю, и веса, с которыми они связаны, не будут обучаться! Решение состоит в приведении входов к значениям ±½ и добавлении смещения к сжимающей функции, чтобы она также принимала значения ±½. Новая сжимающая функция выглядит следующим образом:

 . 

С помощью таких простых средств время сходимости сокращается в среднем от 30 до 50%. Это является одним из примеров практической модификации, существенно улучшающей характеристику алгоритма.

В [13] описана методика применения обратного распространения к сетям с обратными связями, т. е. к таким сетям, у которых выходы подаются через обратную связь на входы. Как показано в этих работах, обучение в подобных системах может быть очень быстрым и критерии устойчивости легко удовлетворяются.

3.4.3 Применения нейросетей обратного распространения

Обратное распространение было использовано в широкой сфере прикладных исследований. Фирма NEC в Японии объявила, что обратное распространение было ею использовано для визуального распознавания букв, причем точность превысила 99%. Это улучшение было достигнуто с помощью комбинации обычных алгоритмов с сетью обратного распространения, обеспечивающей дополнительную проверку.

В работе [14] достигнут впечатляющий успех с Net-Talk, системой, которая превращает печатный английский текст в высококачественную речь. Магнитофонная запись процесса обучения сильно напоминает звуки ребенка на разных этапах обучения речи.

В [15] обратное распространение использовалось в машинном распознавании рукописных английских слов. Буквы, нормализованные по размеру, наносились на сетку, и брались проекции линий, пересекающих квадраты сетки. Эти проекции служили затем входами для сети обратного распространения. Сообщалось о точности 99,7% при использовании словарного фильтра.

В [16] сообщалось об успешном применении обратного распространения к сжатию изображений, когда образы представлялись одним битом на пиксель, что было восьмикратным улучшением по сравнению с входными данными.

4 ПРОГНОЗИРОВАНИЕ КАК ЗАДАЧА РАСПОЗНАВАНИЯ ОБРАЗОВ

4.1 Задача распознавания образов

Распознавание образов - это одна из трудноформализованных задач, решение которой можно выполнить использую нейросеть.

Пусть существует конечное множество графических образов, которые нужно распознать, и соответствующие им двоичные коды желаемых выходов (идентификаторов). В совокупности мы получили обучающее множество, в котором каждому графическому образу соответствует двоичный идентификатор. Спроецируем каждый образ на панель и сопоставим ему двоичный код - это код графического образа.

Возьмем какую-нибудь многослойную нейросеть обратного распространения и проведем обучение этой нейросети по вышеописанным правилам: подадим на вход нейросети считанный с панели двоичный код графического образа, а на выход желаемый идентификатор; будем повторять этот процесс до тех пор, пока нейросеть не обучится распознавать все обучающее множество.

После этого нейросеть можно считать способной распознавать образы из обучающего множества без искажений, а также образы, похожие, на те, которые предъявлялись нейросети при обучении.

Решение этой задачи, действительно интересно, так как ранее такие действия мог выполнять только человек.

4.2 Метод windowing

Задача прогнозирования, рассмотренная ранее в разделе 1 и 2 может быть сведена к задаче распознавания образов, описанной выше, для этого применяется метод окон (метод windowing).

Метод windowing позволяет выявить закономерности во временном ряде на основе сведения анализа временного ряда к задаче распознавания образов и последующего ее решения на нейросети, описанным выше способом.

Основная идея метода: вводится два окна, одно из которых входное (input), второе - выходное (output). Эти окна фиксированного размера для наблюдения данных. Окна способны перемещаться с некоторым шагом S. В результате получаем некоторую последовательность наблюдений, которая составляет обучающее множество. Входному окну соответствует вход нейросети, а выходному окну - желаемый образ (идентификатор в терминологии распознавания образов см. 4.1).

5 РАЗРАБОТКА ПРОГРАММНОЙ СИСТЕМЫ ПРОГНОЗИРОВАНИЯ ВРЕМЕННЫХ РЯДОВ

5.1 Обзор объектно-ориентированного программирования в Delphi

Большинство современных языков программирования поддерживают концепцию объектно-ориентированного программирования (ООП). Эта концепция базируется на основных понятиях: классы, объекты, сообщения, наследование и полиморфизм (или позднее связывание). Среда программирование Delphi 5 [17] использует объектно-ориентированный язык Object Pascal.

Классом (class) называется определяемый пользователем тип данных, который включает в себя состояние (представление класса) и некие операции (поведение класса). Класс имеет некоторое количество внутренних данных и несколько методов, существующих в форме процедур или функций.

Объект (object) есть экземпляр класса или, другими словами, переменная, тип которой является класс. Объекты, в отличие от классов реальны в том смысле, что во время выполнения программы они хранятся в памяти.

Класс может иметь любое число полей и методов. Однако хороший стиль ООП требует, чтобы данные в классах были инкапсулированы (скрыты). Для доступа к внутренним данным объекта нужно использовать методы - это уменьшает шансы появления ошибочной ситуации, а также позволяет автору класса модифицировать его структуру в следующих версиях. Концепция инкапсуляции весьма проста: нужно просто думать о классе как о "черном ящике" с очень маленькой видимой частью. Эта видимая часть называется интерфейсом класса и позволяет получать доступ к данным объектов этого класса остальным частям программы. Для доступа к внутренним данным используются методы - этот подход в концепции ООП называют разграничением информации. Object Pascal заимствовал из C++ три спецификатора доступа: privat (информация доступна только для методов самого класса), protected (доступ разрешен для методов класса и его потомков) и publuc (всеобщий доступ). Есть также спецификатор published, который имеет специальное применение в Delphi.

Object Pascal позволяет определить новый класс, производя его из уже существующего для того, чтобы выразить аналогии между классами. Эта операция называется наследованием и является одной из фундаментальных элементов ООП.

Сообщением называют определенное воздействие одного объекта на другой с целью вызвать соответствующую реакцию. При классическом подходе объекты должны обмениваться только сообщениями.

Полиморфизм - это свойство ООП, при котором одно и то же сообщение может вызывать различные действия на этапе выполнения.

Delphi содержит множество стандартных подпрограмм, но еще больше и важнее имеющаяся библиотека классов VCL (Visual Component Library, библиотека визуальных компонентов), которая имеет иерархическую структуру (иерархия классов). Каждый класс этой иерархии является наследником класса TObject, который является корнем иерархии, что позволяет использовать тип TObject в качестве замены для типа данных любого системного класса. Такая иерархическая структура удобна для программиста и позволяет быстро разрабатывать приложения.

5.2 Объектно-ориентированный анализ задачи прогнозирования на искусственных нейронных сетях

5.2.1 Графический пользовательский интерфейс приложения

Для удобного обращения с создаваемой прогнозируемой системой необходимо разработать удобный и понятный графический интерфейс (см. рисунок 5.1), который должен позволять вводить различные входные данные, управлять работой программы и в удобной форме выводить результат. Все эти действия должны совершаться на форме (окне Windows), поэтому будем использовать объект класса TForm1, наследуемый от базового класса форм TForm.

В поставленной задаче (см. раздел 1), зная алгоритм ее решения (см. раздел 3), выделим входные и выходные данные, а также проанализируем и определим их, используя объектно-ориентированные возможности VCL.

Программа должна выполнять прогнозирование временного ряда, значит необходимо задать временной ряд, для чего нужно указать количество значений в этом ряде и задать собственно значения. Количество элементов может быть только целым и положительным числом, поэтому для его ввода выбираем класс TSpinEdit, который является визуальным компонентом Delphi, а значит, может быть помещен на форму и непосредственно участвовать в диалоге с пользователем. В зависимости от введенного значения количества элементов нужно указать эти элементы. Для решения этой проблемы будем использовать визуальный объект - строковую сетку класса TStringGrid, которая также может быть помещена на главную форму и непосредственно участвовать в диалоге. При помощи этой сетки мы будем также выводить прогноз.

Для задания параметров искусственной нейронной сети обратного распространения поместим на главную форму визуальный компонент класса TSpinEdit (для задания количества слоев в нейронной сети), визуальный компонент класса TStringGrid (для задания количества нейронов в каждом слое нейронной сети).

Для задания параметров алгоритма обратного распространения (см. п. 3.4) и метода windowing (см. п. 4.2) поместим на форму следующие визуальные компоненты: три компонента TSpinEdit для задания размера входного окна (выходное окно будет иметь единичный размер в нашем приложении), для указания количества элементов временного ряда для анализа (на этих элементах нейронная сеть будет обучаться) и для задания количества элементов временного ряда, которые нужно спрогнозировать; два компонента TEdit для задания погрешности обучения нейросети и для задания шага скорости обучения (см. 3.4.2.2.1). Кроме того, поместим на форму переключать, указывающий на необходимость выполнения нормализации временного ряда перед обучением, группу радиокнопок, определяющих тип результирующего прогноза, а также кнопку для запуска процесса обучения и кнопку для выполнения заданного типа прогноза. Для удобного анализа прогноза поместим на форму компонент TeeChart, инкапсулирующий возможность построения диаграмм.

Все описанные выше компоненты являются объектами классов VCL, поэтому они имеют свойства и методы, могут обрабатывать и посылать сообщения. Главная форма содержит все эти объекты в себе, то есть они описаны как поля класса TForm1, а значит, создание объекта класса TForm1 выделяет память под все эти компоненты.

5.2.2 Моделирование нейронной сети обратного распространения

Нейронную сеть обратного распространения можно рассматривать как объект, однако, она в свою очередь состоит из слоев, каждый их которых также может выступать объектом, а каждый слой состоит из отдельных нейронов, которые могут являться объектами. Поэтому способов описания нейросети существует большое количество.

Принципиально правильным было бы описать нейрон отдельным классом, который имел бы свойства (входы, весовые коэффициенты, выход и др.) и действие, которое заключалось бы в вычислении выхода в зависимости от входа. При обучении нейросети необходимо корректировать весовые коэффициенты нейронов, поэтому нужны методы в классе нейрона, которые позволили бы корректировать приватные значения весовых коэффициентов. Затем, нужно описать класс слоя нейросети, содержащего список объектов класса нейронов, и, наконец, создать класс нейросети.

Можно поступить иначе - создать класс нейросети, инкапсулирующий поведение и состояние всей нейросети в целом. Этот подход в меньшей мере отвечает строгой концепции ООП, однако, он выглядит более простым для моделирования нейросети на последовательном вычислителе.

Операционная система Windows 98 является многозадачной операционной системой, поэтому можно было бы класс нейрона сделать наследником класса TThread, создать нить для каждого объекта этого класса, и таким образом промоделировать параллельность работы нейрона в рамках операционной системы Windows 98. На самом же деле все расчеты будут выполняться на одном процессоре (если, конечно, нет многопроцессорной системы), и поэтому нити будут получать процессорное время последовательно, а значит, нет большой необходимости создавать нити, тем более, что в большинстве случаев возникают дополнительные трудности с распараллеливанием: синхронизация вычислений, и такие приложения зачастую на одном процессоре работают медленнее чем последовательные аналогичные алгоритмы, выполняющиеся в одной задаче.

Поэтому, после ряда опытов, было принято решение о создании класса, инкапсулирующего нейросеть обратного распространения вцелом. Этот класс назван TBackPropagation и помещен в модуль bkpropag.pas. Объект этого класса будет моделировать работу нейросети в создаваемой системе прогнозирования. Следует отметить, что эти объекты можно использовать и для других задач, требующих применение нейросетей обратного распространения (класс оптимизирован именно для задачи прогнозирования), при этом нет необходимости в написании программного кода моделирования нейросети, так как он уже инкапсулирован в классе TBackPropagation, и если нужно добавить что-либо к нейросети, то можно воспользоваться наследованием (см. п.5.1).

5.2.2.1 Константы и типы модуля bkpropag

Для корректной работы объекта класса TBackPropagation необходимы следующие константы и типы, которые описаны в интерфейсной части модуля bkpropag (см. приложение А):

·        MAXLAYERS=300 - максимальное количество слоев в нейросети;

·        MAXVES=300 - максимальное количество нейронов в слое;

·        MAXINPUT=300 - максимальное количество входов нейросети;

·        MAXTRAND=300 - максимальное количество элементов во временном ряду;

·        TVesCountNeuro - тип количества нейронов в слоях;

·        TVesNeuro - тип значений весов нейросети;

·        TTrend - временной ряд;

·        TOutPromezh - промежуточные выходные сигналы в нейросети.

5.2.2.2 Описание класса TBackPropagation

Класс TBackPropagation инкапсулирует работу нейросети обратного распространения. В приложении А приводится описание этого класса. Приватные поля содержат данные, описывающие состояние нейронной сети, и некоторые методы, используемые внутри нейросети:

·        fCountLayer:word - количество слоев в нейросети;

·        fArrayVesCount:TvesCountNeuro - количество нейронов в слоях;

·        fArrayVes:TvesNeuro - значения весов нейросети;

·        fXCount:word - количество входных сигналов;

·        fY:double - выходной сигнал нейросети;

·        fCountTrend:word - количнство чисел во временном ряду;

·        fTrend:Ttrend - временной ряд;

·        fYPromezh:ToutPromezh - промежуточные выходные сигналы;

·        procedure RandomVes - задание весов случайным образом;

·        function activation (g:double):double - функция активации;

·        function activation_diff(g:Double):double - производная функции активации.

Интерфейсная часть класса (общедоступные методы) содержит функции установки и считывания состояния нейросети, функции выполнения распознавания и обучения.

Функция SetArrayVesCount задает количество нейронов в слоях и возвращает true при правильной работе, она имеет такие параметры: Count содержит количество слоев нейросети; Xcount равняется количеству входных сигналов для нейросети; AVC типа TVesCountNeuro задает количество нейронов в каждом слое. Функция GetArrayVesCount возвращает результат типа TVesCountNeuro, который содержит массив количества нейронов в слоях нейросети, кроме того, в параметре Count возвращается количество слоев, в параметре XCount количество входных сигналов.

Функция SetTrend задает обучающее множество (временной ряд) и возвращает true при правильной работе, параметр Count содержит количество элементов для обучения, параметр ST типа TTrend задает массив элементов обучающего множества. Функция GetTrend возвращает массив элементов обучающего множества, а также в параметре Count возвращается количество этих элементов.

Функция DoOnePrognoz не имеет параметров и выполняет одношаговый прогноз, на основании данных временного ряда (обучающего множества). Функция DoPrognoz также выполняет прогнозирование, но исходные данные необходимо передать параметром X типа TTrend.

Функция Education выполняет обучение нейросети обратного распространения, при этом нейросети будет обучаться с погрешностью указанной в параметре epsilon и со скоростью, равной параметру alpha.

Кроме вышеперечисленных функций, интерфейсная часть класса TBackPropagation  содержит конструктор класса, в котором выполняется инициализация необходимых параметров нейросети, и свойство для чтения CountLayer, которое содержит количество слоев нейросети.

5.2.3 Диаграмма классов и шаблон основного класса

Существует несколько графических способов представлять результаты объектно-ориентированного проектирования программы. В нашем случае рассмотрим графическую нотацию предложенную Гради Бучем [18]. На рисунке 5.2 приводится диаграмма классов во Гради Бучу.

Рисунок 5.2 - Диаграмма классов

Диаграмма не предоставляет всей информации о классе, поэтому для более детального описания класса применяют шаблоны классов.

Прогнозы, выполненные с помощью искусственных нейронных сетей, являются достаточно достоверными. Многошаговое прогнозирование показывает большую погрешность, так как оно опирается не на реальные данные, а на прогнозные величины. Одношаговое прогнозирование более точно, однако, его нельзя применять для выполнения долгосрочных прогнозов.

Искусственные нейронные сети предложены для задач, простирающихся от управления боем до присмотра за ребенком. Потенциальными приложениями являются те, где человеческий интеллект малоэффективен, а обычные вычисления трудоемки или неадекватны.

Имеется много впечатляющих демонстраций возможностей искусственных нейронных сетей: сеть научили превращать текст в фонетическое представление, которое затем с помощью уже иных методов превращалось в речь [14]; другая сеть может распознавать рукописные буквы [15]; сконструирована система сжатия изображений, основанная на нейронной сети [16]. Все они используют сеть обратного распространения – наиболее успешный, по-видимому, из современных алгоритмов.

Мы продемонстрировали, что искусственные нейронные сети способны решать также задачу прогнозирования путем сведение ее к распознаванию образов. Выполнили прогнозирование курса гривны к доллару на основании данных 2001 года.

Однако, обратное распространение не свободно от проблем. Прежде всего, нет гарантии, что сеть может быть обучена за конечное время. Много усилий, израсходованных на обучение, пропадает напрасно после затрат большого количества машинного времени. Когда это происходит, попытка обучения повторяется – без всякой уверенности, что результат окажется лучше. Нет также уверенности, что сеть обучится наилучшим возможным образом. Алгоритм обучения может попасть в «ловушку» так называемого локального минимума и будет получено худшее решение.

Разработано много других сетевых алгоритмов обучения, имеющих свои специфические преимущества. Некоторые из них обсуждаются в [2]. Следует подчеркнуть, что никакая из сегодняшних сетей не является панацеей, все они страдают от ограничений в своих возможностях обучаться и вспоминать.

Мы имеем дело с областью, продемонстрировавшей свою работоспособность, имеющей уникальные потенциальные возможности, много ограничений и множество открытых вопросов. Для улучшения существующих сетей требуется много основательной работы. Должны быть развиты новые технологии, улучшены существующие методы и расширены теоретические основы, прежде чем данная область сможет полностью реализовать свои потенциальные возможности.