Оригинал документа находится по адресу: http://www.vibrotek.com/russian/med/index.htm

О ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ СОВРЕМЕННЫХ МЕТОДОВ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ В МЕДИЦИНЕ

А.В. Барков, С.В. Дерпгольц

АО ВАСТ,
Россия, 198095, C-Петербург, ул Розенштейна, д. 22

Введение

Многие из достижений техники являются следствием изучения закономерностей жизнедеятельности и поведения живых организмов и, в частности, человека. Проблемами переноса этих закономерностей в технику занимается целая область науки - эргономика. В то же время новейшие достижения в технике достаточно быстро находят применение в медицине. Прежде всего это относится к методам и средствам измерения и анализа различных процессов, а также воздействия на человека с целью лечения или восстановления его работоспособности. В последние годы качественные изменения произошли в технической диагностике машин и энергетического оборудования, основой которых стали новые методы анализа колебательных процессов и. прежде всего, компьютерного анализа модулированных вибрации и шума. Естественным следствием таких изменений стала попытка использовать эти методы для медицинской диагностики.Краткому анализу новых методов и средств анализа акустических колебаний, которые могут использоваться для изучения биоритмов человека, а также описанию возможностей нового программно-аппаратного комплекса "Ариадна" посвящается настоящая публикация.

1. ПРОСТЕЙШИЕ МОДЕЛИ КОЛЕБАНИЙ, ИСПОЛЬЗУЕМЫЕ В ДИАГНОСТИКЕ

Большинство процессов, анализ которых дает основной объем диагностической информации, имеют колебательный характер. В технике это механические, электромагнитные и другие виды колебаний. В биологии и медицине - ритмы, циклы и т.д.
Многие годы основными способами получения диагностической информации являлся анализ формы колебаний или их спектральный анализ.
Если имеют место периодические колебания простой формы, например, гармонические, то успешно могут использоваться оба вида анализа (рис.1).
Информация о колебании в этом случае содержится в его периоде (частоте), величине (амплитуде) и фазе.

Рис.1 Форма гармонических колебаний и их спектр

Если колебания являются результатом сложения нескольких составляющих с разным периодом, более удобно анализировать его спектр (рис.2). Соответственно, и информация о суммарных колебаниях содержится в каждой из составляющих в виде значений величин периода, амплитуды, формы (соотношения амплитуд на кратных частотах) и фазы.

Рис.2 Форма и спектр колебаний, содержащих составляющие с двумя разными периодами.

Если же колебания имеют один период, но сложную форму, более удобно анализировать форму колебаний, при необходимости накладывая временные отрезки сигнала друг на друга (рис.3)

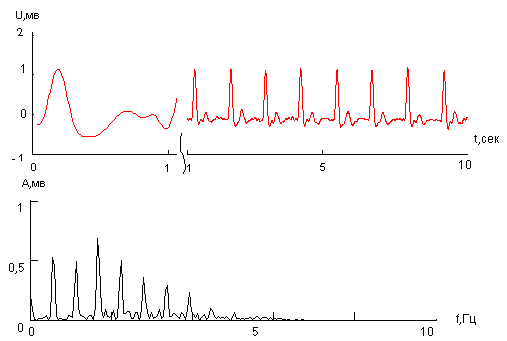Рис.3 Форма и спектр пульсовой волны как периодического сигнала сложной формы.

Особенностью многих видов колебаний в биологических объектах является сложность их формы, поэтому в медицине и биологии наиболее часто используется анализ формы колебаний. Для примера на рис. 4 приведена электрокардиограмма человека. Сигнал с электрокардиодатчика имеет сложную форму, и в нем можно выделить ряд зубцов, несущих информацию о работе сердечно-сосудистой системы.

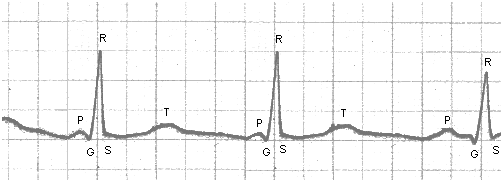Рис.4 Типичная форма кардиосигнала.

Диагностическая информация содержится прежде всего в амплитудах разных зубцов электрокардиограммы и их соотношении. При спектральном анализе сигнала получить аналогичную информацию гораздо сложнее. Главная особенность простейших моделей при анализе формы колебаний или их спектральном анализе заключается в том, что колебания рассматриваются как сумма не влияющих друг на друга составляющих, а все преобразования - линейны, то есть позволяют восстановить форму сигнала по спектру и наоборот. В диагностике, как правило, используются и более сложные, нелинейные модели сигналов и методы их анализа. Это позволяет увеличить во много раз объем получаемой диагностической информации, но результат в значительной степени зависит от используемых моделей и методов анализа сигналов.

2. ОСОБЕННОСТИ КОЛЕБАНИЙ В СЛОЖНЫХ МЕХАНИЧЕСКИХ СИСТЕМАХ.

Многообразие видов колебаний в природе связано с тем, что колебания - естественный путь обмена и передачи энергии. С энергетической точки зрения существует два основных вида колебаний - вынужденные и собственные. Для поддержания собственных (обменных) колебаний в системе с двумя накопителями энергии практически не требуется дополнительной энергии из внешнего источника. В качестве примера можно привести колебания камертона, в котором с определенной (собственной) частотой происходит обмен энергией между накопителями потенциальной (упругость) и кинетической (масса) энергией. Лишь незначительная часть энергии требуется на излучение звука, и именно ее необходимо возобновлять для поддержания непрерывных колебаний. Вынужденные колебания можно рассматривать как форму передачи колебательной энергии от источника к потребителю без возврата значительной ее части в источник. Этот вид колебаний далеко не всегда имеет определенную частоту и простую (синусоидальную) форму, и определяется многими характеристиками источника колебательной энергии. При одной и той же амплитуде собственных и вынужденных колебаний затраты энергии на вынужденные колебания во много раз выше.
В простых колебательных системах по частоте собственных колебаний или по ее изменению от измерения к измерению обнаруживаются дефекты накопителей энергии, а по форме вынужденных колебаний - дефекты в источнике колебательной энергии. В сложных механических системах свойства отдельных элементов и их связей существенным образом изменяют характеристики собственных и вынужденных колебаний. Поэтому для качественной диагностики сложных систем недостаточно ограничиваться измерениями и анализом формы и спектра собственных и вынужденных колебаний. Оптимальные методы анализа колебаний сложных систем, позволяющие производить их глубокую диагностику, должны выбираться на базе математических и физических моделей, наиболее полно описывающих влияние основных элементов и связей на формирование и распространение колебаний в системе.
В сложных механических системах, в зависимости от их назначения, используются специальные средства или для снижения вибрации и шума, если последние отрицательно сказываются на работе системы; или для поддержания оптимального уровня колебаний, если они являются неотъемлемой частью технологического процесса. Эти средства, влияя на параметры колебаний, резко усложняют задачи диагностики механических систем. Для решения подобных задач приходится разрабатывать новые, более глубокие методы анализа колебаний.
Так, в большинстве видов машин и оборудования вибрация негативно влияет на их ресурс, а шум - на здоровье обслуживающего персонала. Основными средствами борьбы с вибрацией и шумом являются амортизаторы, ограничивающие передачу вибрации от узлов, где зарождается вибрация, к другим узлам машин и оборудования, и демпфирующие (поглощающие) элементы и покрытия, резко снижающие собственные колебания за счет поглощения энергии в колебательной системе на резонансных частотах.
В результате колебания, измеряемые в доступных местах машин и оборудования, оказываются значительно ослабленными, с измененной из-за многочисленных резонансов формой, и без ярко выраженных резонансных составляющих. Но и в этом случае механическая система сохраняет свое главное свойство - линейность, при котором колебания существуют только на тех частотах, на которых действуют колебательные силы. Это позволяет сохранить в качестве основного способа получения диагностической информации спектральный анализ колебаний.
Однако, если на низких частотах вибрация и шум обычно содержат ярко выраженные гармонические составляющие, отчетливо проявляющиеся и в спектре сигнала (рис. 5), то на высоких частотах сигнал является случайным и в его спектре редко проявляются и гармонические составляющие вынужденных колебаний и резонансные составляющие собственных колебаний.

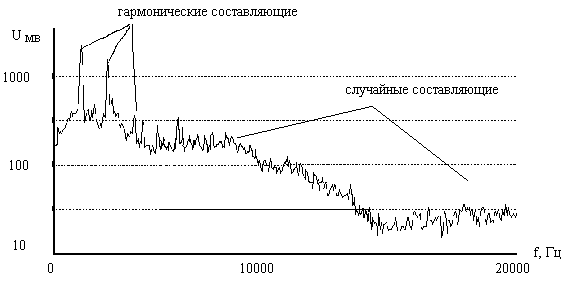Pис. 5 Спектр вибрации машин с несколькими источниками колебаний.

Естественно, что спектральный анализ высокочастотной вибрации машин в такой ситуации практически не дает новой диагностической информации. Поэтому в последние годы вместо спектрального анализа высокочастотных компонент вибрации стали проводить спектральный анализ флуктуаций ее энергии. При таком анализе в спектре предварительно выпрямленного сигнала (сигнала огибающей) гармонические составляющие обнаруживаются лишь тогда, когда мощность высокочастотных случайных компонент вибрации периодически изменяется, как это показано на рис. 6.

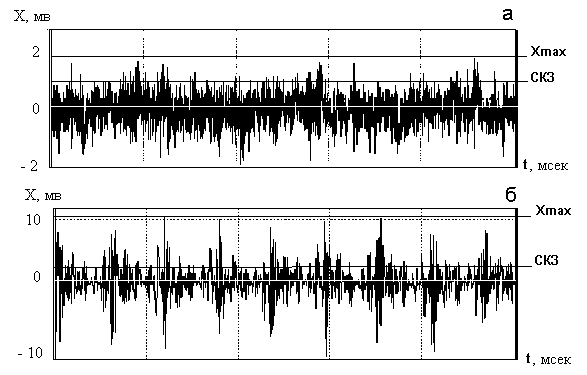Рис. 6а Сигналы высокочастотной вибрации:


a) - сигнал постоянной мощности
б) - сигнал переменной мощности

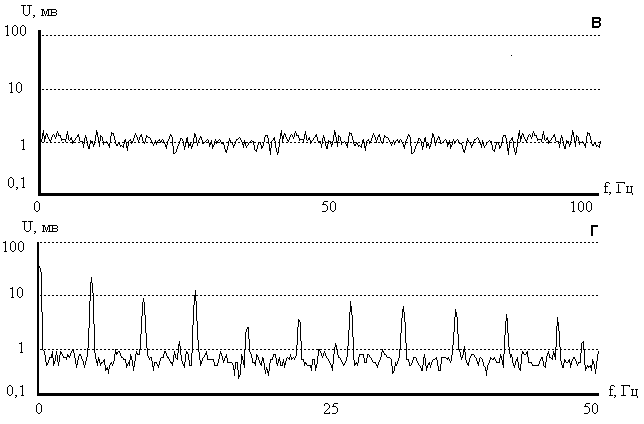Рис. 6б Спектры флуктуаций мощности сигнала (спектры огибающей):


в) - спектр огибающей сигнала постоянной мощности
г) - спектр огибающей сигнала переменной мощности

Как показала диагностическая практика, периодическое изменение мощности, то есть амплитудная модуляция высокочастотных вибрации и шума, появляется лишь при наличии дефектов в источнике их возникновения. В этом случае спектральный анализ огибающей вибрации или шума резко увеличивает объем диагностической информации о состоянии машины, позволяя обнаруживать дефекты на начальной стадии развития.
Кроме машин, имеющих средства борьбы с вибрацией и шумом, достаточно часто встречаются машины и оборудование, в которых вибрация или шум являются частью технологического процесса и поддерживаются на определенном уровне. Как правило, в них используются резонансные (собственные) колебания, а их уровень стабилизируется с помощью систем регулирования с обратной связью, изменяющих частоту колебательных сил в их источнике таким образом, чтобы при любых изменениях свойств колебательной системы обеспечивалось ее совпадение с частотой резонанса системы.
В подобных машинах приходится диагностировать как собственно колебательную систему, так и систему регулирования. Для получения диагностической информации по первой из них обычно используется спектральный анализ колебаний, как наиболее эффективный способ анализа гармонических или резонансных компонент сигнала. А при диагностике систем регулирования с обратными связями используются такие ее свойства, как наличие собственных частот, с которыми они отрабатывают любые изменения в объекте регулирования.
В результате действия таких систем на объект регулирования форма его колебаний усложняется, т.е. колебания на частоте резонанса начинают периодически изменять свою мощность или частоту в небольших пределах. Эта периодичность определяется собственными частотами систем регулирования. Математически результирующие колебания представляют собой мультипликативную смесь компонент с собственными частотами колебательной системы и систем регулирования, т.е. амплитудно и частотно модулированные колебания. На практике для изучения амплитудно модулированных колебаний применяются методы спектрального анализа огибающей, т.е. колебаний мощности сигнала, а для изучения частотно модулированных сигналов - более сложно реализуемые методы спектрального анализа модулирующих процессов.

Таким образом, для диагностики механических систем, как правило, оказывается достаточным использование спектральных методов сигнала и его огибающей. Именно эти методы широко используются в компьютерных системах мониторинга и диагностики различных машин и оборудования по вибрации и шуму, разрабатываемых и выпускаемых, в том числе, и с участием авторов настоящей публикации.

3. МОДЕЛИ СЛОЖНЫХ КОЛЕБАНИЙ В БИОЛОГИЧЕСКИХ ОБЪЕКТАХ

Анализ колебаний в механических системах показал, что в них могут иметь место вынужденные и собственные колебания, причем среди последних чаще встречаются обменные колебания и реже - собственные колебания систем с обратной связью, которые чаще всего переходят в автоколебания. Естественно, что все указанные виды колебаний могут встречаться и в биологических объектах, а кроме того, к ним могут добавляться и другие виды колебаний.
Даже простейший анализ колебаний в биологических объектах показывает, что в них гораздо реже встречаются собственные колебания обменного вида, не требующие больших затрат энергии, и гораздо чаще - собственные колебания систем регулирования с обратной связью. Более того, в биологических объектах глубина регулирования значительно больше, чем в механических, что приводит к появлению такого типа колебаний, как параметрические, редко встречающиеся в механических системах. Естественно, что и методы анализа измеряемых сигналов должны адаптироваться к особенностям и моделям колебаний, применяемых для описания различных процессов в биологических объектах.
Одно из основных отличий в свойствах колебаний механических систем и биологических объектов относится к вынужденным колебаниям, особенно низкочастотным. В механических системах имеющиеся средства борьбы с низкочастотными колебаниями недостаточно эффективны, поэтому в любой точке колебания являются суммой составляющих, сформированных в разных элементах системы, и имеют весьма сложную форму. Соответственно основным методом изучения свойств колебаний в механических системах является их спектральный анализ. В биологических объектах даже низкочастотные колебания по мере удаления от источника быстро затухают, чему способствует активная борьба с колебаниями путем управления свойствами объекта с использованием различного рода систем обратной связи.

Таким образом, в оптимально выбранных точках контроля форма колебаний биологических объектов определяется особенностями функционирования их источника, и анализ формы колебаний дает больше информации, чем спектральный анализ. Именно поэтому например, в кардиологии основным является анализ формы кардиосигнала (рис. 4).
Однако, как показывают исследования, многочисленные системы регулирования с обратными связями оказывают влияние в том числе и на функционирование источников вынужденных колебаний в биологических объектах. Это влияние проявляется, прежде всего, в модуляции вынужденных колебаний, которая убедительно иллюстрируется на примере пульсограммы здорового человека (рис. 7).

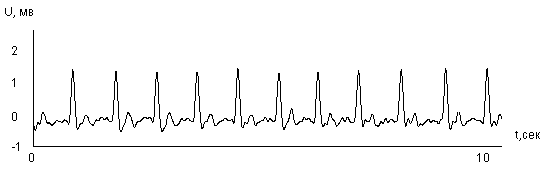Рис. 7 Пульсограмма, измеренная датчиком давления,и иллюстрирующая наличие флуктуаций интервалов и амплитуд в пульсовой волне.

Как видно из пульсограммы, и амплитуда пульсовой волны, и расстояние между ее пиками изменяются во времени на величину, превышающую ошибки измерений. Эти изменения интервалов и амплитуд приведены в увеличенном масштабе на рис. 8.

Рис. 8 Флуктуации интервалов и амплитуд в пульсограмме.

Модуляцию амплитуды пульсовой волны можно рассматривать как флуктуации мощности колебаний и, по аналогии с высокочастотными колебаниями в механических системах, исследовать ее с помощью спектрального анализа колебаний мощности (спектральный анализ огибающей колебаний). Очевидно, что этот же подход может быть использован и для исследования флуктуаций интервалов между пиками пульсовой волны.
При фазовой и амплитудной модуляциях модулирующие процессы, пример которых показан на рис. 8, состоят из нескольких компонент, каждая из которых представляет собой собственные колебания одной из систем регулирования. Такие модулирующие колебания имеют место на разных частотах и в хронобиологии называются собственными биоритмами. В то же время среди наблюдаемых компонент модулирующих процессов могут встретится и те, которые определяются не собственными частотами систем регулирования, а внешними периодическими воздействиями. Эти компоненты, определяющие периодические изменения свойств биологических объектов, в хронобиологии принято называть циклами. К ним относятся суточные, месячные, годовые и другие циклы.
Колебания интервалов между ударами сердца (R-R интервалов) или соответствующие колебаниям интервалов между пиками пульсовой волны давно используются для оценки работы системы регуляции человека. Сначала это была общая оценка в виде среднего размаха колебаний (1), в дальнейшем стал производиться спектральный анализ этих колебаний. На рис. 9 приведен типичный спектр колебаний R-R интервалов, который широко используется в ряде медицинских исследований [2]. Совместный анализ флуктуаций интервалов между пиками и флуктуаций амплитуд этих пиков пульсовой волны (или электрокардиосигнала) смог несколько расширить объем получаемой информации о работе систем регулирования.

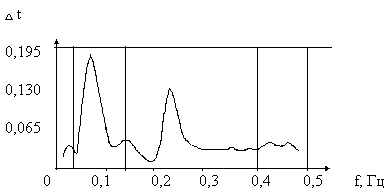Рис. 9 Спектры флуктуаций R-R интервалов сердечного ритма.

Даже графический анализ флуктуаций R-R интервалов в кардиосигнале или пульсовой волне (рис. 8), показывает, что эти колебания нельзя считать не только гармоническими, но и суммой нескольких гармонических компонент, т.е. эти флуктуации, даже если представляют собой собственные колебания нескольких систем регулирования, то обязательно учитывают взаимное влияние одних систем регулирования на другие. Как следствие изменяются частота и форма компонент этих флуктуаций, и, соответственно, их спектральный анализ не дает достаточно полной диагностической информации о системах регулирования.

В этой ситуации исследователи колебаний в биологических системах традиционно переходят на анализ формы сигнала, в частности, представляющего собой флуктуации R-R интервалов, предлагая для этого различные, в основном непараметрические, методы анализа сигналов. Наибольшего успеха в таком анализе добились психиатры (3), занимающиеся изучением связи формы этого сигнала с проявлениями нарушения психики, сопровождающимися изменениями в системах регулирования различных органов и систем человека.
По алгоритмам непараметрического анализа флуктуаций R-R интервалов, предложенных профессором Б.С. Фроловым, с участием авторов настоящей публикации была создана система мониторинга психофизиологического состояния "Пульсар", которая до настоящего времени достаточно успешно используется для контроля за психофизиологическим состоянием операторов ответственных технических систем, а также для оценки воздействия на это состояние внешних факторов, в том числе и лекарственных препаратов.
При проведении испытаний системы "Пульсар" в различных условиях было обнаружено, что предложенные алгоритмы непараметрической обработки сигнала, представляющего собой флуктуации R-R интервалов между ударами сердца, наиболее эффективно работают в тех случаях, когда в сигнале доминирует одна из составляющих собственных колебаний системы регулирования, и тогда результаты анализа формы колебаний оказываются наиболее полными. Однако, у большинства пациентов в подобном сигнале присутствуют, как правило, несколько сравнимых по величине компонент, каждая из которых имеет свой период и свою форму, существенным образом влияющих на форму результирующего сигнала.

Специалисты ассоциации ВАСТ провели расширенные исследования по разработке новых непараметрических алгоритмов анализа сигналов, частично сохраняющих свойства спектрального преобразования Фурье и одновременно позволяющих анализировать форму каждой из компонент сигнала, имеющих разные периоды (частоты). Такие алгоритмы и программное обеспечение стали основой комплекса "Ариадна", предназначенного для анализа модулированных вынужденных колебаний в биологических объектах, в частности электрокардиосигналов и пульсовых волн. Комплекс позволяет анализировать параметры как фазовой модуляции (флуктуаций R-R интервалов), так амплитудной модуляции (флуктуаций амплитуд электрокардиосигналов или пульсовых волн), и решать ряд диагностических задач, связанных с работой систем регулирования. Результаты анализа сигнала, представляющего собой пульсовую волну, приведены ниже (рис.10).

Рис. 10 Результаты спектрального анализа и анализа формы сигнала, представляющего собой флуктуации интервалов (а, б) между пиками пульсовой волны и флуктуации их амплитуд (в, г).

Информативными параметрами при таком анализе чаще всего бывают величины (амплитуды) и периоды (частоты) каждой из обнаруживаемых компонент фазовой и амплитудной модуляции, а также коэффициенты формы и ширины спектральных составляющих. Кроме того, дополнительные данные могут быть получены из сравнениия идентичных признаков, полученных для двух видов (фазовой и амплитудной) модуляции измеренных сигналов.

4. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ РЕЗУЛЬТАТОВ АНАЛИЗА МОДУЛИРОВАННЫХ КОЛЕБАНИЙ ДЛЯ ДИАГНОСТИКИ БИООБЪЕКТОВ

Предложенные модели модулированных колебаний отличаются от моделей колебаний в механических системах. Методы их анализа могут использоваться для мониторинга и функциональной диагностики биологических объектов, в частности человека. Естественно, что для тестовой диагностики с использованием внешних источников колебаний, например ультразвуковых, рентгеновских и т.д. используются другие модели колебаний и методы их анализа. Аналогичная ситуация возникает и при решении задач локализации источников излучения (колебаний) в биологическом объекте, например, методами энцефалографии, томографии и другими, где также используются свои модели колебаний и методы их анализа.
Модели модулированных колебаний, как показали длительные исследования, наиболее успешно описывают функционирование сложных объектов, включающих в себя группу источников колебаний и каналы их передачи, охваченные глубокими обратными связями, изменяющими свойства не только источников колебаний, но и каналов их передачи. Такие модели помогают исследовать характеристики и свойства систем регулирования без вмешательства в их работу, в частности без размыкания систем обратной связи. Изучение формы колебаний и, особенно, ее искажений из-за управления параметрами каналов передачи этих колебаний дает возможность обнаруживать даже незначительные отклонения от нормального функционирования сложных систем регулирования.

Основной особенностью предложенных моделей сигналов и методов их анализа является то, что в большинстве случаев в первом приближении достаточно исследовать колебания, формируемые только в одном из источников, входящих в биологический объект, так как основные системы обратной связи влияют на свойства объекта в целом и, через это влияние, на параметры всех источников колебаний. Как показывают результаты анализа процессов, модулирующих электрокардиосигналы или пульсовую волну человека, находящихся в различном физиологическом и эмоциональном состояниях, характеристики этих процессов, являющихся следствием различного функционирования систем регулирования, претерпевают значительные качественные и количественные изменения.

Рассмотрим те из возможных нарушений в системах регулирования, которые могут быть обнаружены по характеристикам процессов, модулирующих вынужденные колебания в биологических объектах.

Во-первых, это появление автоколебаний в одной из систем регулирования. При этом в модулирующем процессе резко возрастает собственная составляющая, определяемая частотой автоколебаний, а форма этой составляющей приближается к синусоидальной, т.е. коэффициент формы оказывается близким к единице. В качестве примера на рис. 11 приведены спектры и коэффициенты формы модулирующих пульсовую волну процессов у человека с сильной наркотической зависимостью.

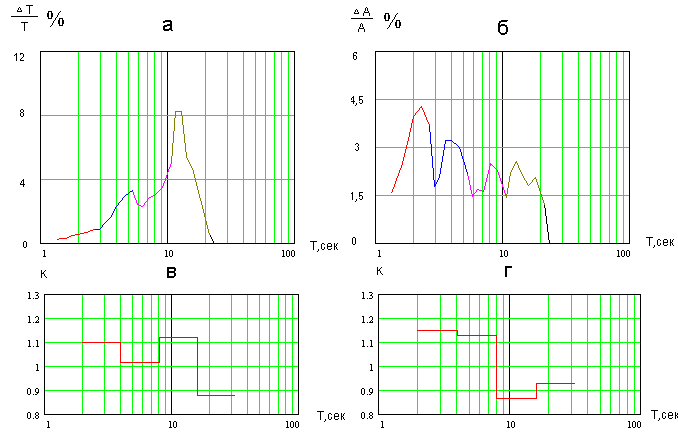Рис 11. Спектры (а, б) и коэффициенты формы составляющих (в, г) процессов, модулирующих RR интервалы и амплитуды пульсовой волны человека с наркотической зависимостью.

Можно определить типовые границы для составляющих этого процесса у людей одной возрастной группы без подобной зависимости. Как видно из рисунка, глубина регулирования интервалов пульсовой волны с периодом модуляции порядка 12 секунд резко возросла и существенным образом превысила подобную границу,также как и глубина регулирования амплитуды этой волны превысила границу, но с периодом модуляции около 3 сек.

Во-вторых, это снижение глубины регулирования сразу в нескольких системах регулирования. У человека чаще всего это связано с усталостью или длительным психологическим перенапряжением. В этом случае весь спектр модулирующих пульсовую волну процессов снижается по величине.

В-третьих, это снижение глубины регулирования в большинстве систем регулирования и, в некоторых случаях, одновременное увеличение глубины регулирования в одной из систем. Как правило это связано с донозологическими изменениями системы регулирования организма человека с одновременной перестройкой всех систем регулирования, направленной на оптимизацию функционирования с учетом защиты от развития болезни. В спектрах модулирующих функций это проявляется в снижении компонент на большинстве собственных частот и в росте компонент на тех частотах, которые относятся к системе регулирования пораженных органов.

В-четвертых, это различие в спектрах процессов, отвечающих за амплитудную и фазовую модуляцию вынужденных колебаний, например пульсовой волны. На рис. 12 приведены коэффициенты формы и спектры модулирующих пульсовую волны процессов, измеренных у человека, находящегося в состоянии сильной усталости.

Рис. 12 Результаты спектрального анализа флуктуаций RR интервалов (а) и амплитуд (б), а также анализа формы компонент этих флуктуаций (в, г) человека в состоянии выраженного утомления.

Как видно из приведенных на рис. 12 графиков, ряд составляющих на одних и тех же частотах достаточно сильно различается в спектрах фазовой и амплитудной модуляции как по величине, так и по форме. Причиной этого могут быть не только изменения в работе систем регулирования, но и различные поражения органов и систем.

Наконец, в-пятых, соотношение величин и форм составляющих фазовой и амплитудной модуляции пульсовой волны или кардиосигнала в значительной степени отражает специфические особенности работы систем регулирования, непосредственно определяющие поведение и личностные свойства человека, в том числе с проявлениями пограничных изменений в психике.

Рис. 13 Общий вид комплекса "Ариадна".

Вся необходимая информация для выявления перечисленных особенностей работы сиистем регулирования может быть получена с помощью измерительно - диагностического комплекса "Ариадна" (рис. 13), который призван помочь специалистам на более высоком уровне оценивать психофизиологическое состояние человека по кардиосигналам или по пульсовой волне.

Любая диагностическая задача предполагает наличие пороговых значений для всех измеряемых параметров. В рассматриваемом случае в качестве измеряемых параметров могут быть:

Пороги для этих величин могут устанавливаться двумя основными способами: или по периодическим измерениям спектров фазовой и амплитудной модуляции колебаний одного и того же объекта контроля (пороги для мониторинга психофизиологического состояния), или по измерениям спектров модуляции колебаний группы объектов, не имеющих патологий и групп объектов с известными патологиями (групповые диагностические пороги).

При дальнейшей отработке комплекса "Ариадна" планируется не только определение пороговых значений для раннего обнаружения различных патологий или групп риска, но и автоматизация решения задач определения этих порогов по выбираемым из базы данных группам объектов диагностики, подбор которых сможет осуществлять пользователь программы "Ариадна".

Выводы

  1. Анализ колебаний, возникающих, как в механических системах, так и в биологических объектах, является одним из основных источников получения диагностической информации. Использование простейших моделей сигналов и методов их анализа приводит к потере значительной части диагностической информации.
  2. Как в механических системах, так и в биологических объектах значительный рост получаемой информации обеспечивается при использовании моделей модулированных колебаний и оптимальных методов их анализа.
  3. Процессы, модулирующие колебания в механических системах и биологических объектах, имеют разную природу и механизм формирования, поэтому и модели модулированных колебаний, и методы их анализа несколько различаются, в первую очередь из-за наличия в биологических объектах развитых систем регулирования многими параметрами.
  4. Основными задачами функциональной диагностики по модулированным колебаниям в механических системах является обнаружение дефектов в источниках колебательных сил, а в биологических объектах - нарушений в работе и отказов систем регулирования.
  5. Для анализа процессов, модулирующих такие колебания в биологических объектах, таких как электрокардиосигналы и пульсовые волны, разработан и выпускается программно-аппаратный комплекс "Ариадна", в котором предусмотрена возможность дополнения его диагностическими программами.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1.Баевский Р.М., Мотылянский Р.Е. - "Ритмы сердца у спортсменов"
Москва "Физкультура и спорт", 1986.

2."Heart rate variability. Standards of measurements, physiological interpretation and clinical use."
European Heart Journal 1996; 17: 354 - 81/

3.Фролов Б.С., Ященко Ю.В. - Авторское свидетельство № SU 1814875 A1
дата приоритета 09.01.81, опубликовано 15.05.93, Бюлл. № 18.

4. Барков А.В., Дерпгольц С.В., Иванов А.С. - "Аппаратно- программный комплекс для оценки текущего психофизиологического состояния человека.","Актуальные проблемы физической культуры в профессиональной подготовке студентов высшей школы."
С-Пб, 1998, стр.37-39